Лабораторная работа № 2-7
Выполнил студент группы ЗАд – 115
Кунин А.В.
К работе допущен
Работу выполнил
Работу защитил
Владимир 2016
2. Цель работы: ознакомление с методом измерения показателя адиабаты для воздуха при адиабатическом процессе расширения и последующем изохорическом нагревании.
3. Оборудование: установка, состоящая из стеклянного баллона с кранами, манометра и осушительного фильтра с порошком хлористого кальция, насоса и секундомера.
4. Теоретическое введение:
Адиабатическим называется такой процесс, который протекает без теплообмена с окружающей средой. Быстропротекающие процессы можно считать адиабатическими, если за время протекания процесса теплообменом рабочего объема с окружающей средой можно пренебречь.
Адиабатический процесс в газе описывается уравнением Пуассона
где P 1 ,V 1 – первоначальные давление и объем газа;
P 2 ,V 2 – давление и объем газа после адиабатического процесса;
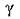
– показатель адиабаты.
Адиабатический процесс на диаграмме P–V изображается кривой 
, называемой адиабатой. Показатель адиабаты равен отношению теплоемкости при постоянном давлении к теплоемкости при постоянном объеме 
Теплоемкостью тела называется отношение элементарного количества тепла 
, полученного телом, к соответствующему приращению dT его температуры 
Если масса тела равна единице массы, то теплоемкость называют удельной. Теплоемкость одного моля вещества называют молярной. Для газов теплоемкость (как удельная, так и молярная) при постоянном давлении больше теплоемкости при постоянном объеме CP > CV, так как при нагревании газа при постоянном давлении (изобарический процесс) подведенное к газу тепло идет на увеличение его внутренней энергии (а следовательно, и температуры) и на совершение газом работы расширения для поддержания постоянного давления. Например, если газ заключен в сосуд с подвижным поршнем, обеспечивающим постоянное давление, то, нагреваясь, он расширяется и поднимает поршень, совершая, таким образом, работу против внешних сил. При нагревании при постоянном объеме (изохорический процесс) все тепло, подведенное к газу, идет на увеличение только его внутренней энергии.
Экспериментальная установка изображена на рис. 1. В стеклянный тонкостенный сосуд А накачивается воздух до некоторого давления P 1, превышающего атмосферное 
, где Р 0 – атмосферное давление; h 1, – избыток давления сверх атмосферного (измеряется водяным манометром М).
Когда воздух в баллоне примет температуру окружающего воздуха T 1, быстро 
открывается клапан К и воздух выпускается наружу до тех пор, пока давление в баллоне не станет равным атмосферному (P 2 =P 0).
Выход воздуха происходит быстро, и, пренебрегая в первом приближении передачей тепла через стенки баллона, процесс расширения воздуха в баллоне можно считать адиабатическим. При этом расширяющийся воздух совершает работу против внешних сил – внешнего атмосферного давления.
Следовательно, температура воздуха в баллоне понижена (до температуры T 2).
После закрытия клапана К давление внутри сосуда начнет возрастать, так как охладившийся при расширении воздух снова нагревается, получая тепло из окружающей среды. Возрастание давления прекратится, когда температура воздуха сравняется с внешней температурой T 1. Окончательное давление 
где h 2 – разность уровней манометра. Происходящие в сосуде процессы представлены на PV диаграмме – на рис. 2.
Температура воздуха в состояниях 1 и 3 одинакова. Согласно закону Бойля – Мариотта
V 1(P 0 + h 1) = V 2(P 0 + h 2)
или
. (1)
В процессе 1-2 произошло адиабатическое расширение газа. Согласно уравнению Пуассона, получим
(2) 
Из (1) и (2) следует
Логарифмирование дает 
Так как давления P 0; P 0 +h 1и P 0 +h 2 незначительно отличаются друг от друга, то в первом приближении логарифмы величин можно заменить их величинами, т.е. искомое значение
(3)
Для вычисления 
по формуле (3) нужно измерить добавочные (относительно атмосферного) давления воздуха в баллоне в 1-м и 3-м состояниях.
5. Методика проведения эксперимента
1. Перед началом работы убедиться в герметичности кранов и мест соединения трубок. Для этого накачайте в сосуд воздух и перекройте кран К. По манометру проследите за изменением давления h 1 в сосуде с течением времени t и постройте график h 1 =f(t). Если установка достаточно герметична, то по истечении некоторого времени 
, необходимого для установления термодинамического равновесия, давление в баллоне перестанет снижаться. В противном случае необходимо найти иустранить течь. Из графика рис. 3 определите время установления термодинамического равновесия
2.Накачайте воздух в сосуд. Выждав время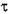 
, измерьте избыточное давление h 1 воздуха в сосуде перед адиабатическим расширением. Затем на короткое время (только до момента выравнивания давлений) откройте кран К (см. рис. 1). Давление в сосуде и температура понизятся (давление до атмосферного, а температура станет ниже комнатной). Температура воздуха в сосуде сравняется с комнатной через время 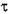, после этого измерьте избыточное давление h 2,. Измерения повторяют 5 – 10 раз.
Величину 
подсчитать по формуле (3) для каждой пары значений h 1 и h 2. Результаты отдельных экспериментов будут заметно отличаться друг от друга. Разброс связан с временем открывания крана К: если кран закроем раньше, чем давление упадет до атмосферного, получим завышенные значения h 2 и ; если кран закроем с опозданием, получим заниженные значения h 2 и . Так как разброс отдельных результатов случаен, вероятным результатом измерения считаем среднее значение.
3. Результаты измерений h 1 и h 2 записать в таблицу. Подсчитать среднее значение . Оценить погрешность двумя способами: как случайную и как погрешность косвенных измерений. Сравнить их. Окончательный результат представить в виде
.
Дополнительное задание
Исследовать влияние времени открывания крана К на получаемый результат. Определить оптимальное время открывания крана К и проанализировать полученные результаты.