
Определение 1. Упорядоченный набор чисел, записанный в виде 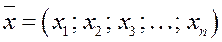 , называется n - мерным вектором, где
, называется n - мерным вектором, где 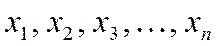 - его координаты или компоненты
- его координаты или компоненты 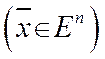 .
.
Понятие n - мерного вектора широко используется в экономике: некоторый набор товаров можно охарактеризовать вектором 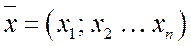 , а соответствующие цены - вектором
, а соответствующие цены - вектором 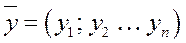 .
.
Векторы можно:
1) умножать на действительное число
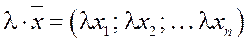 ;
;
2) складывать
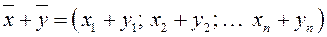 .
.
Эти операции обладают следующими свойствами:
1. 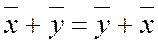 - переместительное (коммутативное).
- переместительное (коммутативное).
2. 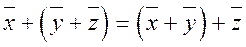 - сочетательное (ассоциативное)
- сочетательное (ассоциативное)
3. 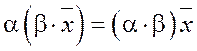 - ассоциативное относительно числового множителя
- ассоциативное относительно числового множителя
4. 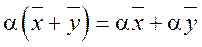 - распределительное (дистрибутивное)
- распределительное (дистрибутивное)
5. 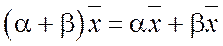 - дистрибутивное относительно суммы числовых
- дистрибутивное относительно суммы числовых
множителей.
6. Существует нулевой вектор 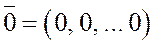 такой, что
такой, что 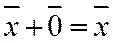
7. Для любого вектора 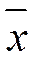 существует противоположный вектор
существует противоположный вектор 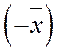 такой, что
такой, что 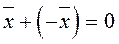
8. 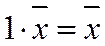 - для любого вектора
- для любого вектора 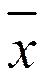 .
.
Определение 2. Множество векторов с действительными компонентами, в котором определены действия 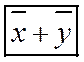 и
и 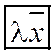 , удовлетворяющие 8- ми свойствам (аксиомам), называется линейнымвекторным пространством.
, удовлетворяющие 8- ми свойствам (аксиомам), называется линейнымвекторным пространством.
§ 10.1 Линейная зависимость векторов.
Определение 1. Вектор 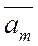 называется линейной комбинацией векторов
называется линейной комбинацией векторов 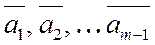 векторного пространства
векторного пространства 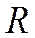 , если он равен сумме произведений этих векторов на произвольные действительные числа:
, если он равен сумме произведений этих векторов на произвольные действительные числа:
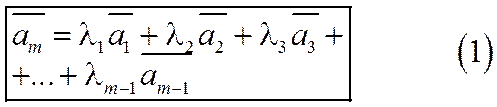
Определение 2. Векторы 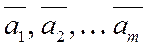 векторного пространства
векторного пространства 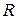 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 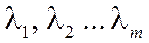 , не равные одновременно нулю, что:
, не равные одновременно нулю, что:
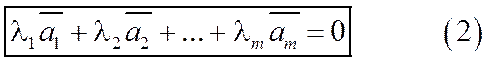
В противном случае векторы называются линейно независимыми (два неколлинеарных вектора).
Пример: Даны три вектора: 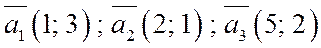 .
.
Доказать, что векторы 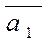 и
и 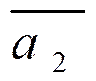 линейно независимы и выразить вектор
линейно независимы и выразить вектор 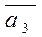 через
через 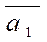 и
и 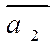 .
.
Решение:
1) Докажем линейную независимость векторов:
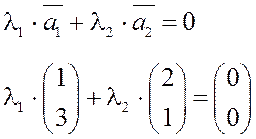
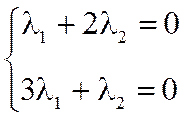
Такая система всегда имеет тривиальное нулевое решение.
|
|
Убедимся, что других решений эта система не имеет:
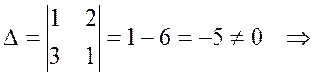 система имеет только нулевое решение, значит, векторы линейно независимы.
система имеет только нулевое решение, значит, векторы линейно независимы.
2)Выразим вектор 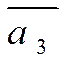 :
:
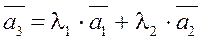
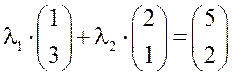
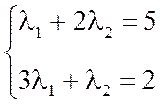
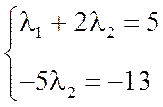
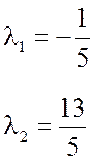
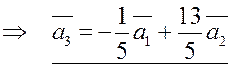
§ 10.2 Базис и размерность линейного векторного пространства.
Определение 1. Линейное пространство R называется n- мерным, если в нем существует n - линейно независимых векторов.
Определение 2. Максимальное число (n) содержащихся в пространстве R линейно независимых векторов называется размерностью пространства и обозначается dim (R).
Определение 3. Совокупность n линейно независимых векторов пространства R называется базисом.
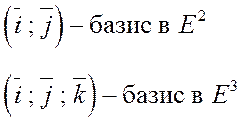
Определение 4. Если 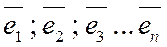 - базис пространства R, то вектор
- базис пространства R, то вектор 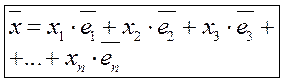 называется разложением вектора
называется разложением вектора 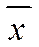 по базису, а числа
по базису, а числа 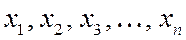 - координатами вектора
- координатами вектора 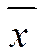 относительно этого базиса.
относительно этого базиса.
§11.Скалярное произведение двух векторов. Евклидово пространство

Определение 1. Скалярным произведением двух векторов 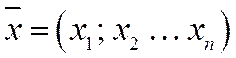 и
и 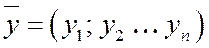 называется число
называется число 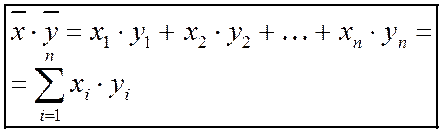
Скалярное произведение имеет экономический смысл: если вектор 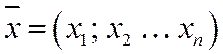 - объем различных товаров, а
- объем различных товаров, а 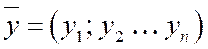 - вектор их
- вектор их
цен, то 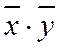 - выражает суммарную стоимость товаров.
- выражает суммарную стоимость товаров.
Скалярное произведение обладает свойствами:
1. 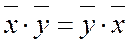 - коммутативность
- коммутативность
2. 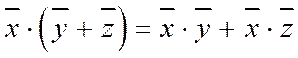 - дистрибутивность
- дистрибутивность
3. 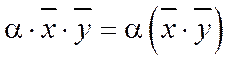 - ассоциативность
- ассоциативность
4. 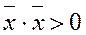 , если
, если 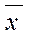 - ненулевой вектор
- ненулевой вектор
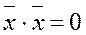 , если
, если 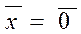
Определение 2. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (аксиомам), называется евклидовым пространством.
Определение 3. Длиной или нормой вектора 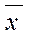 в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
|
|
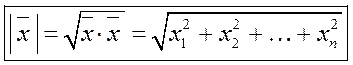
Норма вектора обладает свойствами:
1. 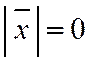 , если
, если 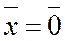
2. 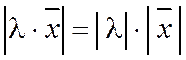 , где λ - действительное число
, где λ - действительное число
3. 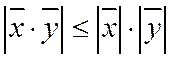 - неравенство Коши-Буняковского
- неравенство Коши-Буняковского
4. 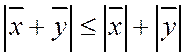 - неравенство треугольника
- неравенство треугольника
В евклидовом пространстве можно тоже находить 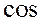 угла между двумя векторами:
угла между двумя векторами:
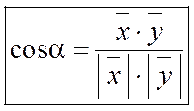 , где
, где 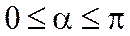 .
.
Из полученной формулы следует, что для n-мерных векторов справедливо определение скалярного произведения, данного для трехмерных векторов.
Определение4: Скалярным произведением двух ненулевых векторов 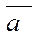 и
и 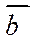 называется число, равное произведению их длин на
называется число, равное произведению их длин на 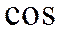 угла между ними.
угла между ними.
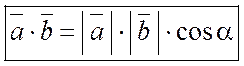
Определение 5. Два вектора называются ортогональными, если их скалярное произведение равно нулю, т.е.
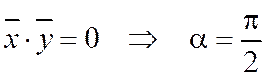
Определение 6. Два вектора считаются коллинеарными если их координаты пропорциональны.
Определение 7. Векторы 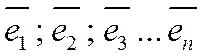 n - мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если
n - мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если
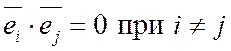 и
и 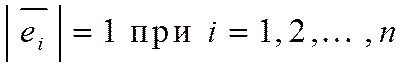
Во всяком n – мерном евклидовом пространстве существует ортонормированный базис.
Пример:
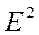 :
: 
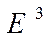 :
: 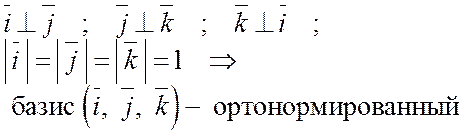
§12. Линейные операторы

Определение 1. Оператором (отображением) линейного векторного пространства называют функцию, определенную на множестве векторов данного пространств и со значениями во множестве векторов пространства:
Определение 2. Оператор 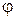 данного пространства называется линейным, если для любых векторов
данного пространства называется линейным, если для любых векторов 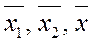 этого пространства выполняются соотношения:
этого пространства выполняются соотношения:
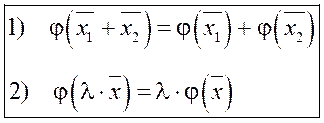
Теорема. Всякая матрица 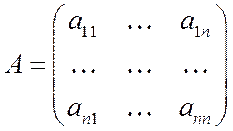 определяет в пространстве
определяет в пространстве 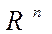 линейный оператор
линейный оператор 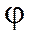 по закону:
по закону:
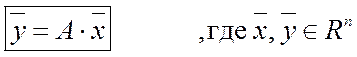
В развернутом виде этот закон можно записать так:
|
|
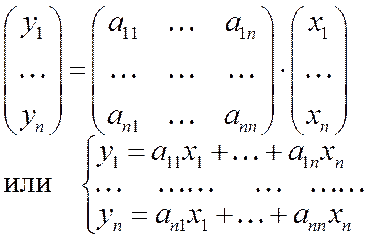
Матрица, о которой говорится в теореме, называется матрицей линейного оператора φ и обозначается 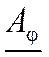 .
.
Равные матрицы задают равные линейные операторы, поэтому линейный оператор, целиком определяется своей матрицей.
Примеры линейных операторов:
1) Нулевой оператор, задаваемый нулевой матрицей:
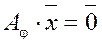 - все векторы переходят в нуль - вектор
- все векторы переходят в нуль - вектор
2) Тождественный оператор 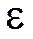 , заданный единичной матрицей
, заданный единичной матрицей 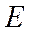 :
:
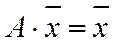 - все векторы переходят в себя
- все векторы переходят в себя
3) Оператор подобия в 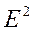 задается матрицей
задается матрицей 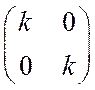 . Этот оператор каждый вектор
. Этот оператор каждый вектор 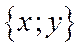 переводит в вектор
переводит в вектор 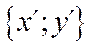 по формулам:
по формулам:
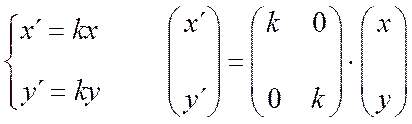
Алгебра линейных операторов
При сложении линейных операторов их матрицы складываются.
При умножении оператора на число, его матрица также умножается на это число.
При умножении операторов их матрицы перемножаются.
Матрица обратного оператора равна обратной матрице исходного оператора.
§13. Собственные векторы и собственные числа линейного оператора
Определение 1. Ненулевой вектор 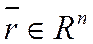 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 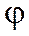 , если под действием
, если под действием 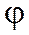 этот вектор переходит в коллинеарный ему вектор
этот вектор переходит в коллинеарный ему вектор 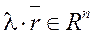 , т.е.
, т.е.
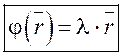 или
или 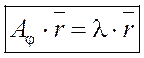
При этом число 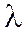 называется собственным числом оператора
называется собственным числом оператора 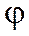 .
.
Займемся теперь вопросом о нахождении собственных векторов и собственных чисел линейного оператора.
Пусть в 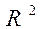 φ:
φ: 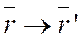 , т.е.
, т.е. 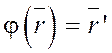 , где
, где 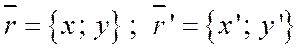
Тогда оператор 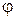 можно задать формулами:
можно задать формулами:
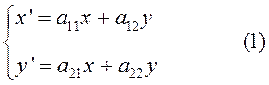 или матрицей
или матрицей 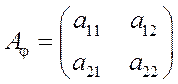 .
.
Для того, чтобы 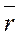 был собственным вектором с собственным числом λ,
был собственным вектором с собственным числом λ,
нужно чтобы 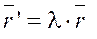 , т.е.
, т.е. 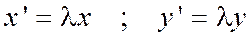
Подставляя эти формулы в систему (1), получим:
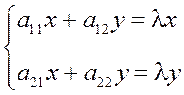 или
или 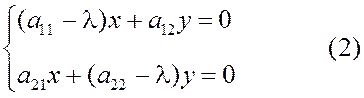 .
.
Полученной системе (2) должны удовлетворять координаты собственных векторов и собственные числа. Эта система однородная, следовательно, она имеет ненулевое решение при условии 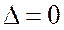 . Таким образом:
. Таким образом:
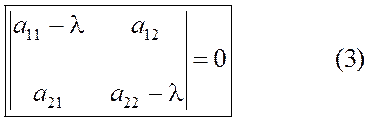 .
.
Это так называемое характеристическое уравнение оператора 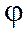 , из которого можно находить собственные числа
, из которого можно находить собственные числа 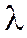 , а затем, используя систему (2), находить собственные векторы, соответствующие этим
, а затем, используя систему (2), находить собственные векторы, соответствующие этим 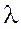 .
.
Характеристическое уравнение часто записывают в более компактной форме. Преобразуем левую часть:
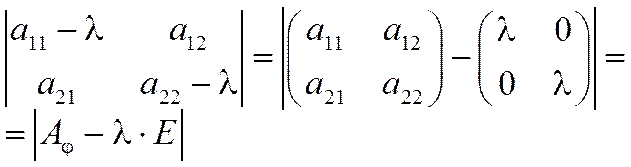 .
.
Получим: 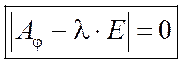 - характеристическое уравнение.
- характеристическое уравнение.
Пример: Найти собственные векторы и собственные числа линейного оператора 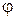 , заданного формулами:
, заданного формулами:
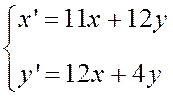
Решение:
1) Составляем характеристическое уравнение:
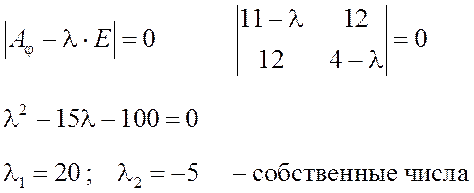
2) Для нахождения собственных векторов составляем систему (2):
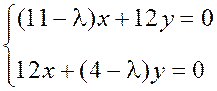
а) при 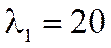
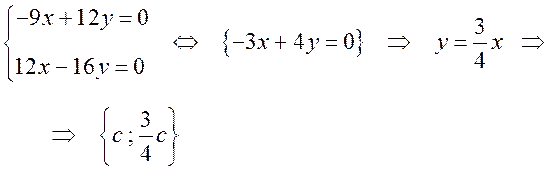
Таким образом, числу 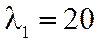 соответствует семейство свободных векторов
соответствует семейство свободных векторов 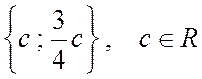 ;
;
б) при 
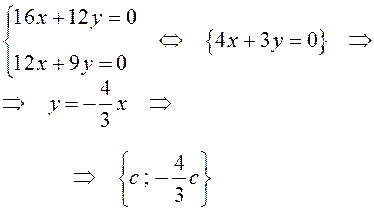
Значит, собственному числу  соответствует подпространство
соответствует подпространство
свободных векторов 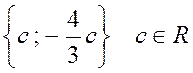
Ответ: имеем собственные числа 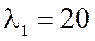 ;
; 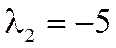 и соответствующие семейства свободных векторов
и соответствующие семейства свободных векторов 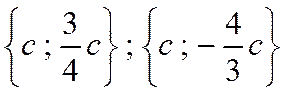 .
.
Отметим, что приведенные рассуждения аналогичны и для 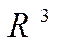 и
и 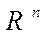 .
.