ЛЕКЦИЯ 13
Тема: «Истечение жидкости через отверстия и насадки»
Весьма важным для практических расчетов гидромеханических систем есть вопрос истечения жидкости через отверстия и насадки. Случаи истечения жидкости через отверстия и насадки встречаются и используются в технике очень широко, назначение их различно. Этим объясняется разнообразие форм отверстий и насадок, используемых в инженерном деле.
В гидромашинах и различных измерительных приборах (в частности расходомерах) распространены местные сопротивления при перетекании жидкости из одного объема в другой через отверстие в тонкой стенке (диафрагму, шайбу и т.д.). На этом мы остановимся несколько позже. А сейчас рассмотрим особенности истечения жидкости через отверстия и насадки.
Истечение жидкости через отверстия
Характер истечения зависит от условий, в которых оно происходит. Различают несколько случаев истечения жидкости из отверстий: при большом относительном напоре, при малом относительном напоре, при переменном напоре. Если тело погружено глубоко или над отверстием большой столб жидкости, то в отверстии будет действовать большой напор, если тело на поверхности, то напор будет малым при том же диаметре отверстия. Истечение может происходить через малое отверстие или большое в тонкой или толстой стенке.
Рассмотрим истечение жидкости из малого отверстия при установившемся режиме.
Если линейные размеры отверстия значительно больше толщины стенки и последняя не влияет на форму струи и характер истечения, стенка называется тонкой. Это имеет место, если δ < 3d, где δ – толщина стенки (рис. 13.1).

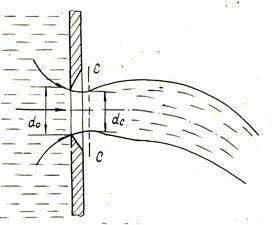
Рис. 13.1
Если толщина стенки соизмерена с размерами отверстия, и последняя влияет на характер течения жидкости, стенка называется толстой. В этом случае δ >> 3d.
Отверстие считается малым, если его высота (или диаметр) меньше 0,1H (d < 0,1H), где Н – напор в центре отверстия (рис. 13.2). При таком условии скорости движения жидкости в различных точках сжатого сечения струи с–с практически одинаковы. При d > 0,1H отверстие считается большим.
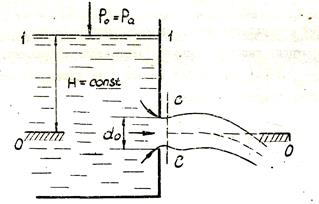
Рис. 13.2
При истечении жидкости из отверстия в сечении с-с на расстоянии (0.5…1)d происходит сжатие струи.
Сжатие струи в непосредственной близости от стенки обусловлено тем, что при обтекании кромок отверстия частицы жидкости стремятся сохранить первоначальное направление своего движения и оказываются под воздействием центробежных сил. За сжатым сечением, в результате трения о воздух и некоторого снижения скорости, струя несколько расширяется согласно уравнению неразрывности
υS = const,
где υ – средняя по сечению струи скорость;
S – площадь живого сечения струи.
При падении струи скорость ее частиц увеличивается за счет действия ускорения свободного падения g, и поэтому струя снова сужается.
Отношение площади сжатого сечения струи Sc к площади отверстия So называется степенью (коэффициентом) сжатия струи:
 , (13.1)
, (13.1)
для круглого отверстия:  , (13.2)
, (13.2)
где dc, do – соответственно диаметр сжатого сечения струи и диаметр отверстия.
Расход жидкости из отверстия Qo может быть определен с помощью уравнения Бернулли, составленного для двух сечений потока: 1-1 и с-с. Принимаем плоскост ь сравнения 0–0 по осевой линии отверстия (рис. 13.2).
Полагаем, что po 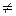 pc
pc 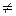 pa, где pa – атмосферное давление, pc – давление в сечении с-с.
pa, где pa – атмосферное давление, pc – давление в сечении с-с.
Тогда уравнение Бернулли примет вид 
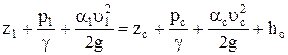
Или 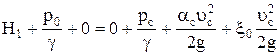 , (13.3)
, (13.3)
где  - потери напора в отверстии, м.
- потери напора в отверстии, м.
Из уравнения (13.3) определяем среднюю скорость в сжатом сечении струи:
 , (13.4)
, (13.4)
где 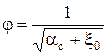 - коэффициент скорости.
- коэффициент скорости.
Из уравнения неразрывности потока
Q0 = Qc = υcSc. (13.5)
Тогда, учитывая уравнение (13.1), получим
Q0 = εS0υc (13.6)
Подставляя υc из уравнения (13.4) в уравнение (13.6), получим формулу для определения расхода жидкости через отверстие
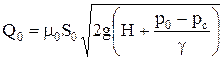 , (13.7)
, (13.7)
где μ0 = εφ - коэффициент расхода жидкости через отверстие.
Уравнение (13.7) является общим уравнением расхода жидкости при истечении ее из малого отверстия.
В том случае, когда р0 = рa, и истечение идет в атмосферу, т.е. рс = рa
Q0 = μ0S0  . (13.8)
. (13.8)
В общем случае коэффициент расхода μ0 при Н = const зависит от формы отверстия, числа Рейнольдса и степени сжатия струи. Степень сжатия струи в свою очередь зависит от формы и размеров емкости и от расположения отверстия относительно ее стенок.
В связи с этим различают три типа сжатия: совершенное, несовершенное и неполное (рис. 13.3).
Совершенное сжатие имеет место, когда отверстие находится на значительном расстоянии от направляющих стенок, и они не оказывают влияние на сжатие струи (рис. 13.3, отверстие I). В этом случае сжатие струи будет наиболее полным и всесторонним. Значение коэффициентов ξ0, ɛ, μ0, γ, данные в гидравлических справочниках, соответствуют совершенному сжатию струи:
μ0 = 0,62; ɛ = 0,64; ξ0 = 0,05…0,06.
|
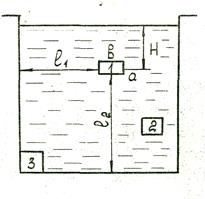
Рис. 13.3
Если направляющие стенки оказывают влияние на истечение жидкости через отверстие, то сжатие называется несовершенным (рис. 13.3, отверстие 2).
Коэффициент расхода в этом случае может быть определен по формуле:
μнес = μ0(1 + k),
где μ0 - коэффициент расхода при совершенном сжатии;
k = 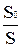 - отношение площади отверстия к площади стенки бака.
- отношение площади отверстия к площади стенки бака.
Если какая-либо кромка отверстия не совпадает с направляющей стенкой емкости, сжатие струи называется неполным (рис. 13.3, отверстие 3).
Коэффициент расхода при неполном сжатии μнеп определяют по приближенной зависимости академика Н. Н. Павловского
μнеп = μ0(1 + 0,4 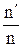 ),
),
где n – весь периметр отверстия;
 - часть периметра отверстия, по которой сжатие струи устранено направляющей стенкой.
- часть периметра отверстия, по которой сжатие струи устранено направляющей стенкой.
Таким образом, μ0 < μнес < μнеп.
В зависимости от формы отверстия поперечное сечение вытекающей струи будет различно. Так при истечении через квадратное отверстие форма вытекающей струи будет крестообразной, а через треугольное – с тремя тонкими ребрами.
Истечение жидкости под уровень (затопленная струя)
Расход через затопленное отверстие (рис. 13.4) определяется по формуле
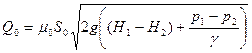 . (13.9)
. (13.9)

Рис. 13.4
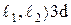 .
2. Несовершенное:
.
2. Несовершенное: 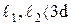 .
3. Неполное:
.
3. Неполное:  или
или 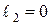 .
2. Несовершенное:
.
2. Несовершенное: