Парадокс Бертрана Рассела
В наиболее общей форме парадокс Бертрана Рассела выглядит так:
Пусть М - множество всех множеств, которые не содержат себя в качестве своего элемента.
Вопрос: содержит ли М само себя в качестве элемента?
Если ответ «да», то, по определению М, оно не должно быть элементом М и мы получили противоречие.
Если ответ «нет» - то, по определению М, оно должно быть элементом М - вновь противоречие…
«В чём же суть противоречия? Класс иногда является, а иногда не является членом самого себя. «Класс чайных ложек, например, не является другой чайной ложкой, но классы вещей, не являющиеся чайными ложками, являются одними из вещей, которые не являются чайными ложками».
Парадокс Рассела связан с использованием понятия класса всех собственных классов. «Собственным» называется класс, не содержащий себя самого в качестве своего элемента. «Несобственным» - класс, который, по предположению, содержит себя самого в качестве своего элемента. Полагают, что таков класс всех классов. Относительно класса всех собственных классов («расселовского класса») и ставится вопрос: каков он - собственный или несобственный? Если предположить, что он собственный, то он должен быть отнесён к несобственным классам, и наоборот.
В полушутливой форме Рассел представляет этот парадокс через однотипный, так называемый парадокс «Брадобрея» во «Введении в философию математики» (1919). Деревенский брадобрей должен брить всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя? Если он будет брить себя, значит, он бреется сам и не имеет права брить себя. Но если он не будет брить себя, он имеет право себя брить. Таким образом, можно продемонстрировать и парадоксальность «множества всех множеств, не являющихся собственными элементами». Надо отметить, что «Брадобрей» - не «чистый парадокс», ибо из него следует только, что такого парикмахера вообще не может существовать, т. е. «принципиально не может быть найдена никакая однозначная и непротиворечивая определённость для этой совокупности, содержащая элементы, определимые только в терминах этой совокупности, а также элементы, включающие в себя или предполагающие эту совокупность». Устраняется парадокс заключением, что если некоторые предпосылки рождают противоречие, значит они неверны.
Антиномия Рассела сыграла важную роль в развитии оснований математики. Она подорвала основы теории множеств, саму новую логику, стала истинным бедствием и крушением надежд тех, кто занимался проблемами обоснования математики и логики на рубеже XIX-XX веков.
Вопрос 2. Операции над множествами
Рассмотрим основные операции над множествами
Объединениеммножеств A и B называется множество A∪B={x|(x∈A)∨(x∈B)}.
Например, если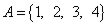 
, 
, 
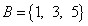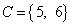, то 
, 
, 
.
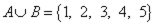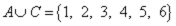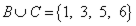Пересечениеммножеств и называется множество A∩B={x|(x∈A)∧(x∈B)}.
Например, если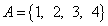 
, 
, 
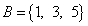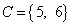, то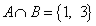 
, 
, 
.
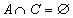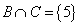Множество, состоящее из всех элементов множества A, не принадлежащих множеству B, называется разностью множеств A и B: A∖B={x|(x∈A)∧(x∉B)}.
Например, если 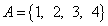, , 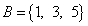, 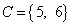то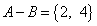 
, 
, 
, 
.
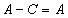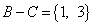
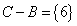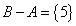Если A⊂B, то B∖A называют дополнением множества A до множества B:AB′.
Если, в частности, A− подмножество некоторого универсального множества U, то разность U∖A обозначается символом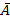 
или A′ и называется дополнением множества A (до множества U).
Из определения дополнения множества следуют равенства A∪A′=U;A∩A′=∅,(A′)′=A.
Симметрической разностью множеств A и B называют множество AΔB, состоящее из тех и только тех элементов, которые принадлежат только одному из множеств A или B, то есть
AΔB=(A∖B)∪(B∖A).
Для любых подмножеств A и B множества U справедливы следующие равенства, которые называют законами двойственности или законами де Моргана:
(A∪B)′=A′∩B′; (A∩B)′=A′∪B′.
Примеры: Доказать справедливость равенств
1) (A∩B)′=A′∪B′
Доказательство.
x∈(A∩B)′⇔x∉(A∩B)⇔x∉A∨x∉B⇔x∈A′∨x∈B′⇔x∈(A′∪B′)⇔(A∩B)′=A′∪B′.