Подача поршневого насоса зависит от площади поршня и от величины его перемещения во время нагнетания.
 ,
,
где 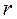 – радиус кривошипа;
– радиус кривошипа;
 – угол поворота кривошипа;
– угол поворота кривошипа;
 – текущее значение хода поршня.
– текущее значение хода поршня.
Если поршень переместиться на величину  , то:
, то:
 ,
,
 ,
,
где 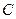 – скорость поршня.
– скорость поршня.
 ,
,
 ,
,
 ,
,
 .
.
Подача насоса за один оборот (поршня) коленчатого вала равна объёму цилиндра:

Подача при непрерывном вращении:
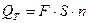 .
.
С учётом кратности действия:
 .
.
Для насосов двух- и четырёхкратного действия учитывается объём, занятый штоком.
Действительная подача:
 ,
,
 – рабочий объём цилиндра насоса простого действия,
– рабочий объём цилиндра насоса простого действия,
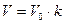 – насоса многократного действия.
– насоса многократного действия.
Выше показано, что подача поршневого насоса является величиной переменной, т.к. поршень движется с переменной скоростью, а жидкость при нормальных условиях действия неотрывно следует за поршнем. Это можно показать, построив график подачи. Площадка под кривой (0-6’) равна элементарной подаче насосов, следовательно, вся площадь под кривой (0-6’) равна подаче насоса за один ход поршня.
Вывод: подача насоса простого действия – величина переменная, равна Ø в начале и конце хода нагнетания и имеет максимум в средней части хода нагнетания, когда  . Подача насоса простого действия отличается неравномерностью.
. Подача насоса простого действия отличается неравномерностью.
Неравномерность оценивается величиной отношения:
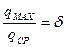 ,
,
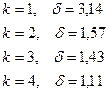
где:
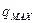 – максимальная секундная подача насоса,
– максимальная секундная подача насоса,
 – средняя подача.
– средняя подача.
Степень неравномерности подачи зависит от кратности действия.
Лекция 14
Напор поршневых насосов
Напором насоса называют приращение энергии, сообщённое насосом единице массы жидкости. Для поршневого насоса это приращение равно разности энергии жидкости и её напора под поршнем во время нагнетания и всасывания:
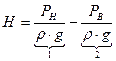 .
.
1 – напор жидкости во время нагнетания,
2 – напор жидкости во время всасывания.
При выводе выражения для этих параметров, учитывают переменную скорость движения жидкости, используя уравнение неустановившегося движения жидкости, которое описывает изменение энергии единицы массы жидкости при её движении на участке бесконечно малой длины:

1 – изменение удельной энергии жидкости, т.е. энергии единицы массы невязкой идеальной жидкости, движущейся с постоянной скоростью.
2 – энергия, затрачиваемая на преодоления гидравлических сопротивлений.
3 – энергия инерционных сил, действующих на жидкость.
Напор под поршнем во время всасывания равен сумме бесконечно малых изменений энергии жидкости по всей длине всасывающего тракта, от приёмного отверстия трубопровода до поршня в данной точке его хода, т.е. получается в результате интегрирования уравнения неустановившегося движения:

Интегрирование происходит почленно, а пределы определяются с помощью схемы.

 – давления на свободную поверхность жидкости в расходной цистерне;
– давления на свободную поверхность жидкости в расходной цистерне;
 – скорость жидкости в направлении приёмного отверстия всасывающего трубопровода;
– скорость жидкости в направлении приёмного отверстия всасывающего трубопровода;
 – высота всасывания;
– высота всасывания;
 – текущее значения хода поршня;
– текущее значения хода поршня;
 – полный ход поршня;
– полный ход поршня;
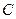 – скорость поршня;
– скорость поршня;
 – напор под поршнем во время всасывания.
– напор под поршнем во время всасывания.
После интегрирования и суммирования результатов, пренебрегая величинами малого порядка, получаем:
 ,
,
где:
1 – напор под поршнем при всасывании; 2 – следствие атмосферного давления,
3 – следствие гидравлического давления во всасывающем тракте,
4 – следствие скорости жидкости и гидравлических сопротивлений всасывающего тракта,
5 – сопротивления всасывающего клапана,
6 – следствие действия инерционных сил на жидкость,
3, 4, 5, 6 – факторы определяющие величину напора при всасывании,
 – приведённый коэффициент гидравлических сопротивлений всасывающего тракта,
– приведённый коэффициент гидравлических сопротивлений всасывающего тракта,
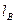 – приведённая длина всасывающего тракта.
– приведённая длина всасывающего тракта.
Решая это уравнения относительно  , принимаем во внимание, что:
, принимаем во внимание, что:
 .
.

Данные для построения  получают в результате суммирования величины составляющих (1-5) с учётом знака.
получают в результате суммирования величины составляющих (1-5) с учётом знака.
 – величина переменная, имеющая минимум в начале и максимум в конце хода всасывания. Ордината между 1 и
– величина переменная, имеющая минимум в начале и максимум в конце хода всасывания. Ордината между 1 и  – потери жидкости во всасывающем тракте на преодоление его сопротивления.
– потери жидкости во всасывающем тракте на преодоление его сопротивления.