Лабораторная работа № 1. Модели на основе разностных уравнений

Цель работы: научиться выполнять в среде Scilab анализ систем, заданных в виде разностных уравнений.

Задание. Показать динамику, построить фазовый портрет и бифуркационное дерево динамической системы, заданной одномерным дискретным отображением.

Таблица 1. – Варианты заданий

№	Дискретное отображение	a	x0
			0,2
			0,2
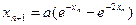
			0,2
		4,5	0,2
			0,2
			0,2
		3,5	0,2
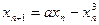
			0,2
		6,7	0,2
		5,5	0,2
			0,2
		4,5	0,2
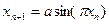
			0,2
		6,5	0,2

Методические указания:.

Отображение – это функция, которая показывает зависимость последующих значений параметров системы от предыдущих значений.

C помощью точечных отображений изучают объекты не с непрерывным, а с дискретным временем.

Дискретное логистическое отображение – это полиномиальное отображение, которое описывает, как меняется численность популяции с течением времени. Его часто приводят в пример того, как из очень простых нелинейных уравнений может возникать сложное, хаотическое поведение.

Математическая формулировка логистического отображения:

, где:

x_n принимает значения от 0 до 1 и отражает численность популяции n -ом году, а x₀ обозначает начальную численность (в год номер 0);

r ‑ положительный параметр, характеризующий скорость размножения (роста) популяции.

Это нелинейное отображение описывает два эффекта:

- с одной стороны, когда численность популяции мала, она размножается со скоростью, пропорциональной этой численности;

- с другой стороны, поскольку популяция обитает в среде с ограниченной «ёмкостью», то при росте плотности популяции скорость размножения падает, возрастает конкуренция и смертность.

Фазовый портрет ‑ это то, как величины, описывающие состояние системы (динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, и т.д.

Фазовый портрет исследуемой системы ‑ это совокупность фазовых траекторий для всевозможных начальных условий, характеризующая состояния и движения динамической системы.

Совокупность точек М(x(t), y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям, называется фазовой траекторией.

Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений.

Бифуркация – эти качественная перестройка картины движения, т.е. скачкообразное изменение качественного поведения системы при плавном изменении параметра. Значения управляющего параметра, при которых происходят бифуркации, называются критическими или бифуркационными значениями.

Бифуркационная диаграмма – это зависимость положения устойчивых состояний x (либо неподвижных точек, либо точек циклов) от значения параметра r. При переходе параметра через критические значения происходят бифуркации.

Под понятием бифуркационная диаграмма подразумевают изображение на рисунке смены возможных динамических режимов системы (равновесных состояний, стационарных точек, периодических орбит и пр.) при изменении значения бифуркационного параметра.

Отчет по лабораторной работе должен содержать:

1. Титульный лист.

2. Задание.

3. Текст программы.

4. Результаты работы программы.

5. Выводы.

Пример выполнения задания

Показать динамику, построить фазовый портрет и бифуркационное дерево динамической системы, заданной одномерным дискретным отображением . Принять а=2 и х₀=0,2.

Программа для построения дискретного отображения и фазового портрета при хаотическом режиме динамики, а также для построения бифуркационной диаграммы в Scilab приведена ниже.

Результаты работы программы Scilab показаны на рисунках 1-3.

Рисунок 1 – Дискретное отображение

Рисунок 2 – Фазовый портрет

Рисунок 3 – Бифуркационное дерево