ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ В ГРАФАХ
Понятия о связности и связных компонентах в неориентированных графах приведено в разделе 1.1. В ориентированном графе существуют аналогичные понятия, характеризуемые достижимостью и различными типами связности. Рассмотрим эти понятия и свойства.
Если существует путь, идущий от вершины xi к вершине xj, то говорят, что вершина xj достижима для вершины xi.
Пусть задан неориентированный граф G =á X, G ñ и его матрица смежности A. Достижимое множество вершин R (xi) для вершины xi - есть множество вершин, которые достижимы для вершины xi. Но, по определению, любая достижимая для xi вершина соединена с ней хотя бы одним путем длины ноль (при i = j), один, два, …, или k £ n. Тогда достижимое множество для xi можно представить в виде:
R (xi) = { xi }È G (xi)È G 2 (xi)È…È G k (xi),
где k имеет такое наименьшее значение, после которого R (xi) уже не изменяется, т.е. не наращивается.
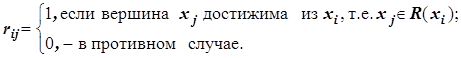 |
Ограниченно достижимое множество обозначают через Rk (xi). Это множество вершин, достижимых путем максимальной длины k (и менее). Тогда полностью достижимое множество R (xi)= Rk (xi), если Rk (xi) =Rk+1 (xi).
Определим матрицу достижимостей R= [ rij ] следующим образом:
При этом i -е строки матрицы достижимостей есть вектора, соответствующие множествам R (xi) в упорядоченном перечислении их элементов.
2.2. Лабораторная работа №2.1: “Поиск связных компонент”
Цель:
Исследовать свойства достижимости и связности вершин в неориентированных графах.
Задание:
· Разработать программу для экспериментального исследования достижимости и связности вершин, а также для выявления связных компонент в неориентированных графах на основе рекуррентных операций с матрицами по заданному варианту:
1) представлять матрицу смежности в виде двумерного массива и использовать формулу логического произведения матриц для исследования ограниченной связности;
2) представлять матрицу смежности одномерным массивом из двоичных векторов; использовать поразрядные операции при вычислении суперпозиции соответствий.
· Исследовать свойства связности неориентированных графов на примере рекомендуемых тестовых графов:
1) гамильтонов путь при n = 10, в котором вершины связаны в порядке их нумерации;
2) граф первого пункта с удаленным пятым ребром;
3) перенумерованный в случайном порядке граф предыдущего пункта; при этом вершины в пути должны следовать не в порядке их нумерации.
· После отладки на указанных тестах для получения исходного графа подключить генератор графа, запускаемый по клавише “Enter”.
Замечание:
Обратите внимание на отличие в результатах тестов второго и третьего пунктов. Объясните суть этого отличия.
Порядок выполнения работы
Требования к алгоритму
Работа рассчитана на 4 часа. При этом требуется разработать Pascal - или C ++ - программу, вычисляющую последовательно (по шагам) степени матрицы смежности A2, А3, …, Ak и соответствующие им матрицы ограниченных достижимостей R2, R3, …, Rk. Вычисления необходимо продолжать до тех пор, пока для некоторого шага k+1 матрица ограниченных достижимостей не совпадет с матрицей ограниченных достижимостей k -го шага, т.е. условием окончания алгоритма является Rk+1=Rk.
Требования к структуре данных
При начальной разработке и отладке программы рекомендуется задавать матрицу смежности и ее порядок в виде констант.
Максимальный порядок матрицы для обоих вариантов работы равен соответственно:
1) 255,
2) 31 для Pascal -программы и 32 для C - программы.
Для первого варианта рекомендуется побайтное представление элементов матрицы смежности и других матриц (см. методические указания для данной работы) как двумерных массивов беззнаковых целых чисел длиной 8 бит. Для второго варианта, с целью повышения эффективности, рекомендуется представлять матрицу смежности и других матриц в виде одномерного массива, состоящего из битовых векторов, как беззнаковых целых данных (для Pascal - программы - просто целых) длинной 4 байта.
Требования к результатам
Исходное состояние экрана соответствует шагу инициализации. Это - нулевой шаг, когда при любой матрице смежности матрица достижимостей определяется множествами R (xi) = { xi }, т.е. Ri = I - есть единичная матрица с единицами только на главной диагонали. Следовательно, на первом шаге следует отобразить в верхней половине экрана нулевую матрицу смежности графа (или опустить ее вывод), единичную матрицу Ri и номер шага n = 0.
На первом шаге результатом является дополнительное отображение двух матриц в нижней половине экрана (матрицы смежности A исходного графа и матрицы ограниченных достижимостей R1 длинной маршрута равного 1) и отображения номера шага k = 1.
На втором шаге результатом является отображение двух матриц в верхней половине экрана (A2 и матрицы ограниченных достижимостей R2 длинной маршрута равного 2) и номера шага k =2, замещая результат нулевого шага.
На третьем и последующих шагах вычисления соответственно матриц смежности А3, A4, … и матриц ограниченных достижимостей R3, R4, … маршрутом длинны k =3, 4, …. При этом полученные результаты следует отображать так, как показано на рис. 2.1:
· для нечетного шага в нижней половине экрана;
· для четного шага в верхней половине экрана.
 |
(а) (б)
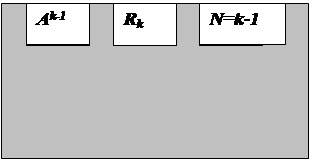 | 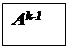 | 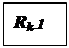 |  | ||||
Рис. 2.1. а) Вид экрана после нечетного шага; б) Вид экрана после четного шага.
Переход к следующему шагу рекомендуем организовать по нажатию клавиши “Пробел” и повторять до тех пор, пока матрицы ограниченных достижимостей и текущего и предыдущего шагов не станут одинаковыми. Выход из программы должен осуществляться либо по достижению k = n либо по “Esc”, когда визуально отмечается это условие.
Замечания:
1. Следует обратить внимание на симметричность получаемых на каждом шаге матриц. Так как исследуемые графы в этой работе - неориентированные, то их матрицы смежности так же - симметричные. Симметричными будут и их суперпозиции, или логические произведения.
2. Окончательная матрица достижимостей должна либо полностью состоять из единиц, либо из нескольких подматриц, заполненных только единицами. Это зависит от связности исследуемого графа. Здесь подматрицей считается некоторое подмножество строк и соответствующих столбцов с указанным свойством. Если эти подмножества следуют подряд друг за другом, то матрица имеет так называемый “блочно-диагональный вид”: блоки из единиц следуют друг за другом по главной диагонали. Такой вид примет матрица достижимостей для второго тестового графа.
Методические указания
При подготовке к работе рекомендуем предварительно ознакомиться в разделе 1.1 с такими понятиями как маршрут, цепь, простая цепь, а в разделе 1.2 - с понятиями связности и связных компонент в графе. В дополнение к этому рассмотрим вопросы алгоритмизации определения связности.
Выразим формулу для достижимого множества в виде рекуррентных соотношений и построим наш алгоритм, последовательно вычисляя накапливающие объединения. На каждом его шаге будем вычислять очередные степени соответствий Г (xi) для всех i =1, 2, …, n и накапливать текущие значения R (xi).
Будем считать k -м шагом алгоритма вычисление k -х степеней соответствий, т. е. { G k (xi) | xi Î X }. Тогда на k -м шаге будем получать множества ограниченных достижимостей { Rk (xi) | xi Î X }, что дает достижимые множества маршрутами длиной не более k. Эти вычисления можно выразить простыми рекуррентными соотношениями: Rk (xi) = Rk (xi) È Rk-1 (xi) для каждого i = 1, 2, …, n.
На каждом шаге такого алгоритма увеличивается порядок ограниченной достижимости. И повторять их следует до тех пор, пока не совпадут результаты двух очередных шагов.
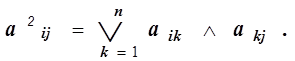 |
Вычисление степеней соответствий на каждом шаге так же можно построить на основе рекуррентного соотношения: Gk (xi) = G (Gk-1 (xi)). Теперь напомним, что каждая i -я строка матрицы смежности задает соответствие G (xi). Значит и суперпозиции соответствий { G2 (xi)= G (G (xi)) | xi Î X } задает логическое произведение матриц A2 = A ´ A, вычисляемое по формуле:
Следовательно, выражение для вычисления матрицы ограниченных достижимостей в общем виде можно представить так:
Rk = A0 È A1 È A2 È…È Ak,
и представим его следующими простыми рекуррентными соотношениями:
Rk = Ak-1 È Rk при k >0;
R0 = A0;
Ak = Ak-1 × A при k >0;
A0 = I.
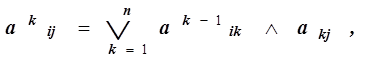 |
На первом шаге алгоритма, при k =1, матрица ограниченных достижимостей будет равна R1 = A0 È A1, где A0 = I - единичная матрица того же порядка, состоящая только из единиц на главной диагонали, а A1 - это матрица смежности исходного графа. Рекуррентное соотношение для вычисления k -й степени матрицы смежности по формуле логического произведения матриц для k = 2, 3, … n имеет вид:
где:
ak j - это элемент матрицы смежности A;
ak-1ik -это элемент предыдущей степени матрицы смежности (k -1 шага), т.е. Аk-1;
akij - это элемент k -й степени матрицы смежности текущего шага, т.е. Ak.
Другим способом вычисления k -ой степени матрицы смежности является прямой, но эффективно реализуемый в программе, матричный способ вычисления степеней соответствий. Для определения i -й строки матрицы текущей степени Ak выполняется поразрядная дизъюнкция тех строк матрицы смежности, номера которых равны единичным разрядам i -ой строки матрицы k -1-й степени предыдущего шага Ak-1.
Результат этой операции может сразу помещаться в i -ю строку матрицы Ak. Это сокращает время за счет поразрядных операций и экономит память. В этом случае отпадает необходимость отводить дополнительный рабочий массив для промежуточного результата. Матрица Ak-1 постепенно преобразуется в Ak в одном и том же массиве. Вычисление матрицы ограниченных достижимостей для k -го шага Rk выполняется путем поразрядной дизъюнкции матриц:
Rk = Rk- 1Ú Ak.
После второго шага экран примет вид, показанный на следующем рисунке (рис. 2.2).
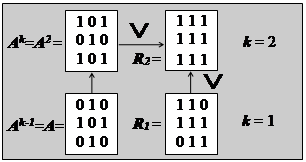 |
Рис. 2.2. Вид экрана на втором шаге и схема основных операций.
2.3. Лабораторная работа №2.2: “Поиск сильных компонент”
Цель:
Исследовать свойство достижимости и связности в ориентированных графах путём выявления сильных компонент.
Задание по вариантам:
1) Выявление сильных компонент в графе на основе вычисления логического произведения матриц.
2) Выявление сильных компонент в графе на основе вычисления степеней соответствий.