Сводный индекс производительности труда (по трудоемкости)
- условная величина, показывающая, какими были бы затраты времени на выпуск данной продукции, если бы трудоемкость не изменилась
- общие затраты времени на выпуск данной продукции в текущем периоде
Пример: (трудоемкость и выпуск продукции на предприятии Х)
| Вид изделия | Затраты врем. на 1 изд., чел | Произв - но, шт | Расчетные графы, чел | |||
янв 
| Фев
| янв 
| Фев 
| 
| 
| |
| А | 0,9 | |||||
| Б | 1,2 | 388,8 | ||||
| В | 0,9 | 0,8 | 676,8 | 601,6 | ||
| Итого | 1515,6 | 1330,6 |
Прирост производительности труда в целом по предприятию составляет 13,9%
Сводный индекс затрат рабочего времени (труда)
Сводный индекс физического объема продукции (реализации) по трудоемкости
Взаимосвязи
Сводный индекс производительности труда в стоимостном выражении (по выработке)
Пример (имеются данные о производительности и отпускных ценах предприятия А)
| Вид продук. | Сентябрь | Октябрь | Оптов. Цена, руб. р | Расчетные графы, руб. | |||
| Произв, шт
| Труд. затраты 
| Произ, шт
| Труд. затраты 
| 
| 
| ||
| А | |||||||
| Б | |||||||
| В | |||||||
| Итого |
В течении периода за 1 чел. вырабатывалось 65,8 руб. продукции, а в базисном – 64,4 руб. прирост производительности 2,2 %.
Взаимосвязи
Другая форма агрегатных индексов – средневзвешенные индексы.
Применяются, когда имеющаяся информация не позволяет рассчитывать агрегатный индекс.
Средний индекс – индекс, вычисленный как средняя величина из индивидуальных индексов.
Средний индекс должен быть тождественен агрегатному.
Используются две формы средних:
1. Арифметическая
2. Гармоническая
Средний арифметический индекс тождественен агрегатному индексу, если веса индивидуальных индексов – слагаемые знаменателя агрегатного индекса.
Средний арифметический индекс физического объема продукции (реализации)
Средний арифметический индекс производительности труда
В средний арифметической форме рассчитывается индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина
Показывает, во сколько раз возрастала (изменилась) производительность труда, или сколько % составлял рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности.
Средние арифметические индексы чаще применяются для расчета сводного индекса количественных показателей.
Индексы качественных показателей определяются по формуле средней гармонической взвешенной величины.
Средний гармонический индекс тождественен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.
Средний гармонический индекс себестоимости
Средний гармонический индекс цен
Пример (по данным о продуктовых товарах в супермаркете)
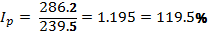
Схема расчета индексов за несколько временных периодов называется системой индексов.
В зависимости от базы сравнения системы индексов бывают:
1. Базисными
2. Цепными
Выбор базы сравнения проводятся в зависимости от цели анализа.
Базовые индексы дают более наглядную характеристику общей тенденции развития исследуемых явлений, а цепные – четче отражают последовательность изменения уровней во времени.
Между цепными и базисными индексами существует различные виды связи:
- Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные
- Если известны последовательные значения базисных индексов, то можно рассчитать на их основе цепные
При построении систем индексов можно использовать постоянные и переменные веса. Постоянные веса позволяют исключить влияние изменения структуры на величину индекса.
Переменные веса – веса отчетного периода
Взаимосвязи
4 варианта системы индексов:
А. Цепные индексы цен с переменными весами:
Б. Цепные индексы цен с постоянными весами: (по Ласпейросу)
В. Базисные индексы цен с переменными весами:
Г. Базисные индексы цен с постоянными весами (по Ласпейросу):
При изучении динамики качественных показателей необходимо определить изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов
Изменением значения индексируемого показателя у отдельных групп единой и измененной структуры явления.
Изменение структуры явления - изменение доли отдельных групп единиц совокупности в общей их численности.
Т.к. на изменение среднего значения показателя оказывают воздействие 2 фактора, возникает задача: определить степень влияния.