Введение.
Сформулируем некоторые факты из теории функций многих переменных, которые понадобятся нам далее.
Определение: функция z=f(u,v) называется дифференцируемой в точке (u, v), если ее приращение Δz представимо в виде:

Линейная часть приращения называется полным дифференциалом и обозначается dz.
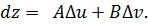
Теорема (достаточное условие дифференцируемости) см[1].
Если в некоторой окрестности т.(u, v) существуют непрерывные частные производные  и
и  , то функция f(u, v) дифференцируема в этой точке и
, то функция f(u, v) дифференцируема в этой точке и
 (du=Δu, dv=Δv). (1)
(du=Δu, dv=Δv). (1)
Определение: Вторым дифференциалом функции z=f(u, v) в данной точке (u, v) называется первый дифференциал от первого дифференциала функции f(u, v), т.е. 
Из определения второго дифференциала z=f(u, v), где u и v – независимые переменные, следует

Таким образом, справедлива формула: 
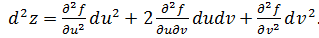 (2)
(2)
При выводе формулы использована теорема Шварца о равенстве смешанных производных  . Это равенство справедливо при условии, что
. Это равенство справедливо при условии, что  определены в окрестности т.(u, v) и
определены в окрестности т.(u, v) и 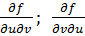 непрерывны в т.(u, v). cм[1].
непрерывны в т.(u, v). cм[1].
Формула для нахождения второго дифференциала может быть записана символически в следующем виде:  – формальное возведение скобки в квадрат с последующим формальным умножением справа на f(x y) дает полученную ранее формулу [1]. Аналогично справедлива формула для 3-го дифференциала:
– формальное возведение скобки в квадрат с последующим формальным умножением справа на f(x y) дает полученную ранее формулу [1]. Аналогично справедлива формула для 3-го дифференциала:
 и вообще:
и вообще:
 , где формальное возведение в n-ую степень производится по формуле бинома Ньютона:
, где формальное возведение в n-ую степень производится по формуле бинома Ньютона:
 ;
; 
Отметим, что первый дифференциал функции двух переменных обладает свойством инвариантности формы. То есть, если u и v — независимые переменные, то для функции z=f(u, v), согласно (1)

Пусть теперь u=u(x y), v=v(x y), тогда z=f(u(x y), v(x y)), x и y — независимые переменные, тогда

Используя известные формулы для производной сложной функции:

Тогда из (3) и (4) получим:
 .
.
Таким образом,
 (5)
(5)
где  — первый дифференциал функции u,
— первый дифференциал функции u,  — первый дифференциал функции v.
— первый дифференциал функции v.
Сравнивая (1) и (5), видим, что формальная запись формулы для dz сохраняется, но если в (1) du=Δu, dv=Δv — приращения независимых переменных, то в (5) du и dv — дифференциалы функций u и v.
Второй дифференциал сложной функции двух переменных.
Прежде всего, покажем, что второй дифференциал не обладает свойством инвариантности формы.
Пусть z=z(u, v) в случае независимых переменных u и v второй дифференциал находим по формуле (2)
Пусть теперь u=u(x y), v=v(x y), z=z(u(x y), v(x y)), где независимые переменные x и y. Тогда
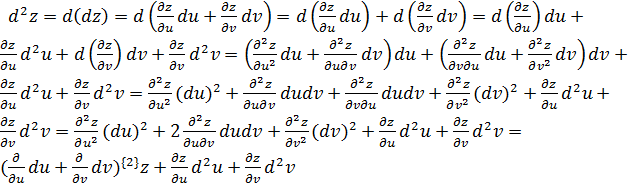 .
.
Итак, мы получили окончательно:

Формулы (2) и (6) не совпадают по форме, следовательно, второй дифференциал не обладает свойством инвариантности.
Ранее были выведены формулы частных производных 1-го порядка для сложной функции z=f(u, v), где u=u(x y), v=v(x y), где x и y — независимые переменные см [1].


Выведем формулы для вычисления частных производных и дифференциала второго порядка для функции z=f(u, v), u=u(x y), v=v(x y), где x и y — независимые переменные.
Для функций u(x y), v(x y) независимых переменных x, y имеем формулы:



Подставим формулы (8) в (6).

Таким образом, получили формулу для дифференциала второго порядка сложной функции двух переменных.

Сравнивая коэффициенты при  для частных производных второго порядка сложной функции двух переменных в (2) и (9), получаем формулы:
для частных производных второго порядка сложной функции двух переменных в (2) и (9), получаем формулы:
.

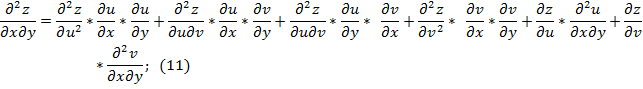

Пример 1 см [2]
Пусть z=f(u, v), u=xy, v=  . Найти второй дифференциал.
. Найти второй дифференциал. 
Решение: вычисляем частные производные:
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
, 
Подставив полученные результаты в (9), получаем ответ:
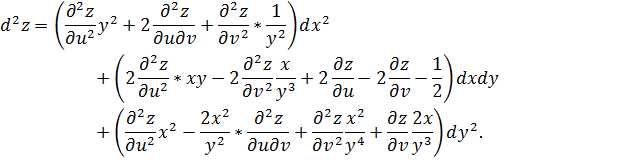
Важные частные случаи.
1. Рассмотрим случай, когда z=f(u, v), u=u(t), v=v(t).
Для первого дифференциала имеем:
 ;
;
Если в формуле (9) положить x≡t и учесть, что все производные по y отсутствуют, то получим:

Отметим, что в квадратных скобках формулы (13) стоит формула производной второго порядка для случая, если z=f(u, v), где u=u(t), v=v(t).
2. Рассмотрим случай, когда z=f(u), где u=u(x y).
Для первого дифференциала имеем:

Далее по формуле (6):

Сравнивая коэффициенты при  , получаем формулы для вторых частных производных:
, получаем формулы для вторых частных производных:

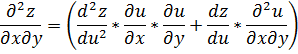
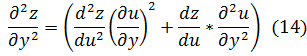
Пример 2 см [3].
Пусть 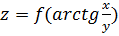 . Найти
. Найти  .
.
Решение: обозначим u=  . Находим частные производные:
. Находим частные производные:
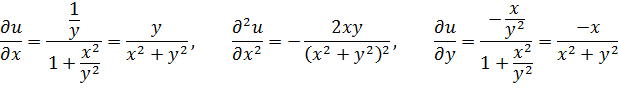

Находим второй дифференциал:

3. Рассмотрим случай, когда z=f(x y), y=y(x).
Для первого дифференциала имеем:

Далее из 1.получаем: 
Список литературы:
1.Архипов Г.И. Садовничий В.А. Чубариков В.Н. Лекции по математическому анализу. М.: Дрофа, 2004
2.Виноградова И.Л. Олехник С.Н. Садовничий В.А. Задачи и упражнения по математическому анализу М.В.Ш., 2002
3.Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука,1990.
Интернет-источники
1.https://sibac.info/conf/naturscience/xxx/41991