Тема занятия: Построение графиков тригонометрических функций
y=sin(x) и у=cos(x).
Задание №1 (20 баллов)
За каждой правильно выполненный пункт 10 баллов.
Инструкция для построения графика тригонометрической функции y=sin(x).
Название функции: тригонометрическая
Название графика: синусоида
Алгебраическая запись: y=sin(x).
Вам понадобиться:
- линейка;
- карандаш;
- знание основ тригонометрии.
Синусоида представляет собой график функции y=sin(x). Синус – ограниченная периодическая функция. Перед построением графика необходимо провести аналитическое исследование и расставить точки.
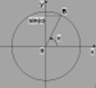
1. На единичной тригонометрической окружности синус угла определяется отношением ординаты “y” к радиусу R. Поскольку R=1, можно рассматривать просто ординату “y”. Она соответствует двум точкам на этой окружности.
 Для будущей синусоиды постройте координатные оси Ox и Oy. На оси ординат отметьте точки 1 и -1. Отрезок для единицы выберите равный 2 клеточки, так как за его пределы функция синуса не зайдет.
Для будущей синусоиды постройте координатные оси Ox и Oy. На оси ординат отметьте точки 1 и -1. Отрезок для единицы выберите равный 2 клеточки, так как за его пределы функция синуса не зайдет.
На оси абсцисс выберите масштаб, число π =3 единицы, следовательно 6 клеточек. π/2=1,5 единицы, следовательно 3 клеточки. Таким образом просчитать все табличные значения до 2π и отметить справа от 0 на оси абсцисс. Потом отметить эти же точки слева на оси абсцисс, только со знаком минус.
2. Составляем таблицу для значений синуса.
При этом помним, что π=3 единицы, а единица = 2 клетки. π=6 клеточек
| х | 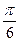
| 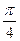
| 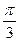
| 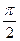
| 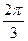
| 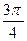
| 
| 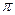
| 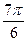
| 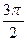
| 
| 
| |
| клеточки по оси Ох | |||||||||||||
| у |
Замечание. 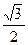 ≈0,9;
≈0,9; 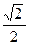 ≈0,7;
≈0,7;
 Осталось лишь плавно соединить полученные точки на графике. Выше оси Ox синусоида будет выпуклая, ниже – вогнутая. Точки, в которых синусоида пересекает ось абсцисс, являются точками перегиба функции. Имейте в виду, что в концах отрезка синусоида не заканчивается, она бесконечна
Осталось лишь плавно соединить полученные точки на графике. Выше оси Ox синусоида будет выпуклая, ниже – вогнутая. Точки, в которых синусоида пересекает ось абсцисс, являются точками перегиба функции. Имейте в виду, что в концах отрезка синусоида не заканчивается, она бесконечна
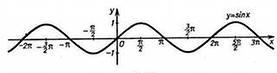
Задание №2 (18 баллов) За каждый выполненный пункт 2 балла
Практическая работа
Свойства функции y=sin(x)
Для этого нужно ответить на вопросы и заполнить таблицу, используя график построенной функции:
| 1. Область определения функции y=sin(x) | D(у)= |
| 2. Область значения функции y=sin(x) | Е(у)= |
| 3. Нечетность, т.е. симметричность относительно начало координат | sin(- x)= |
| 4. Периодичность функции | sin(x+ 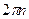 )= )=
|
| 5. Точки пересечения с осью Ох | (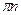 ;0) ;0)
|
| 6. Точки пересечения с осью Оу | |
| 7. Промежутки, где функция принимает положительные значения | |
| 8. Промежутки, где функция принимает отрицательные значения | (- 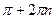 ; ; 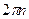 ) )
|
| 9. Промежутки возрастания | 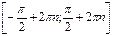
|
| 10. Промежутки убывания | |
| 11. Точки минимума | 
|
| 12. Минимумы функции | -1 |
| 13. Точки максимума | |
| 14. Максимумы функции |
Задание №3 (34 баллов)
20 баллов – инструкция полностью прописана для графика функции у=cos(x) (за каждый выполненный пункт 10 баллов)
14 баллов – график построен правильно (4 баллов – расставлены значения по осям координат; 10 баллов – график построен правильно)
Самостоятельная работа
 Построить график функции у=cos(x).
Построить график функции у=cos(x).
Используя инструкцию для построения графика функции y=sin(x).
Название функции:?
Название графика: синусоида
Алгебраическая запись:?
Задание №4 (28 баллов) За каждый выполненный пункт 2 балла
Свойства функции у=cos(x).
Для этого нужно ответить на вопросы и заполнить таблицу, используя график построенной функции:
| 1. Область определения функции у=cos(x) | D(у)= |
| 2. Область значения функции у=cos(x) | Е(у)= |
| 3. Четность, т.е. симметричность относительно ________________? | cos(- x)= |
| 4. Периодичность функции | cos(x+ 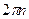 )= )=
|
| 5. Точки пересечения с осью Ох | |
| 6. Точки пересечения с осью Оу | |
| 7. Промежутки, где функция принимает положительные значения | |
| 8. Промежутки, где функция принимает отрицательные значения | |
| 9. Промежутки возрастания | |
| 10. Промежутки убывания | |
| 11. Точки минимума | |
| 12. Минимумы функции | |
| 13. Точки максимума | |
| 14. Максимумы функции |
Критерии оценки:
| Баллы | Оценка |
| 60-79 | |
| 80-89 | |
| 90-100 |
Домашняя работа:
Из плотного картона изготовить шаблон для вычерчивания графика функции y=sin(x) и у=cos(x).(за масштабную единицу принять отрезок, равный 1 см).
Тема занятия: Построение графиков тригонометрических функций
y=tg(x) и у=ctg(x).
Задание №1 (20 баллов)
За каждой правильно выполненный пункт 10 баллов.
Инструкция для построения графика тригонометрической функции y=tg(x).
Название функции: тригонометрическая;
Название графика: тангенсоида;
Алгебраическая запись: y=tg(x).
Вам понадобиться:
- линейка;
- карандаш;
- знание основ тригонометрии.
1. Графика тангенса вначале строим на интервале (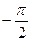 ;
; 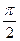 ) аналогично построению, описанному в случае функции синуса
) аналогично построению, описанному в случае функции синуса
Составляем таблицу для значений тангенса.
При этом помним, что π=3 единицы, а единица = 2 клетки. Следовательно π=6 клеточек
| х | 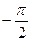
| 
| 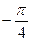
| 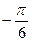
| 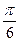
| 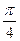
| 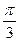
| 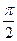
| |
| клеточки по оси Ох | Вертикальная асимптота (вертикальная линия) | Вертикальная асимптота (вертикальная линия) | |||||||
| у | ---- | ---- |
Замечание. 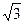 ≈1,7;
≈1,7; 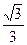 ≈0,6;
≈0,6;
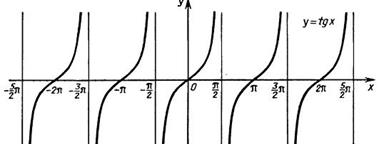 2. Осталось лишь плавно соединить полученные точки на графике. График функции будет стремиться к вертикальным асимптотам, но никогда их не достигнет.
2. Осталось лишь плавно соединить полученные точки на графике. График функции будет стремиться к вертикальным асимптотам, но никогда их не достигнет.
Параллельными переносами вдоль оси ОХ вправо и влево на π, 2π и т.д построить график функции тангенса.
Задание №2 (20 баллов) За каждый выполненный пункт 2 балла
Практическая работа
Свойства функции y=tg(x)
Для этого нужно ответить на вопросы и заполнить таблицу, используя график построенной функции:
| 1. Область определения функции y=tg(x) | D(у)= |
| 2. Область значения функции y=tg(x) | Е(у)= |
| 3. Нечетность, т.е. симметричность относительно начало координат | tg(- x)= |
| 4. Периодичность функции | tg(x+ 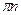 )= )=
|
| 5. Точки пересечения с осью Ох | (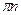 ;0) ;0)
|
| 6. Точки пересечения с осью Оу | |
| 7. Промежутки, где функция принимает положительные значения | |
| 8. Промежутки, где функция принимает отрицательные значения | ( ; ; 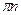 ) )
|
| 9. Промежутки возрастания | 
|
| 10. Промежутки убывания | |
| 11. Точки минимума | нет |
| 12. Минимумы функции | |
| 13. Точки максимума | |
| 14. Максимумы функции |
Задание №3 (32 баллов)
20 баллов – инструкция полностью прописана для графика функции у=ctg(x) (за каждый выполненный пункт 10 баллов)
12 баллов – график построен правильно (2 баллов – расставлены значения по осям координат; 10 баллов – график построен правильно)
Самостоятельная работа
 Построить график функции у=ctg(x).
Построить график функции у=ctg(x).
Используя инструкцию для построения графика функции y=tg(x).
Название функции:?
Название графика: тангесоида
Алгебраическая запись:?
Задание №4 (28 баллов)
За каждый выполненный пункт 2 балла
Свойства функции у=ctg(x).
Для этого нужно ответить на вопросы и заполнить таблицу, используя график построенной функции:
| 1. Область определения функции у=cos(x) | D(у)= |
| 2. Область значения функции у=cos(x) | Е(у)= |
| 3. Нечетность, т.е. симметричность относительно ________________? | ctg(- x)= |
| 4. Периодичность функции | ctg(x+ 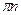 )= )=
|
| 5. Точки пересечения с осью Ох | |
| 6. Точки пересечения с осью Оу | |
| 7. Промежутки, где функция принимает положительные значения | |
| 8. Промежутки, где функция принимает отрицательные значения | |
| 9. Промежутки возрастания | |
| 10. Промежутки убывания | |
| 11. Точки минимума | |
| 12. Минимумы функции | |
| 13. Точки максимума | |
| 14. Максимумы функции |
Критерии оценки:
| Баллы | Оценка |
| 60-79 | |
| 80-89 | |
| 90-100 |
Домашняя работа:
Из плотного картона изготовить шаблон для вычерчивания графика функции y=tg(x) и у=ctg(x)..(за масштабную единицу принять отрезок, равный 1 см).
