Расчётную схему колонны принимаем с шарнирным соединением верха колонны и жёстким соединением низа колонны:
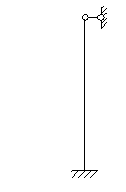Высота (геометрическая) колонны в соответствии с исходными данными имеет величину 5,6 м.
Для принятой расчётной схемы, учитывая п. 7.1.4.4 [1], расчётная длина колонны определяется по формуле 7.17 [1]:
ld = m0 × l,
где m0 - коэффициент, принимаемый по таблице 7.1 [1]. В нашем случае равен 0,8. Тогда ld = 0,8 × 5600 = 4480 мм.
Предварительно принимаем связи между колоннами в виде распорок, устанавливая их на середине высоты колонны, что в свою очередь уменьшает расчётную длину колонны вдвое.
Далее предварительно принимаем следующие размеры колонны:
- ширина сечения по верху b = 150 мм;
- высота сечения по верху hsup = 200 мм;
- ширина сечения по низу b = 150 мм;
- высота сечения по низу hinf = 600 мм.
Колонну проектируем дощатоклееную, состоящую из досок, согласно таблю Б1 [1], сечением 25х150 мм.
Далее определяем положение центра тяжести колонны в её плоскости.
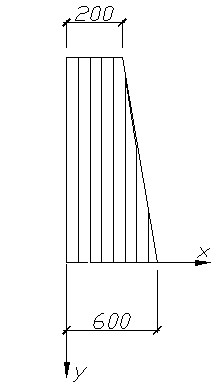Статический момент продольного сечения колонны относительно оси x:
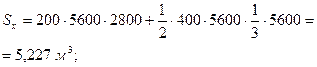
То же относительно оси y:
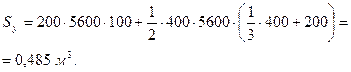
Тогда координаты центра тяжести продольного сечения колонны определим как: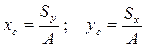 
,
где A - площадь продольного сечения:
;
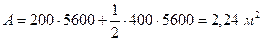Тогда: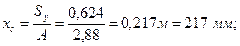 
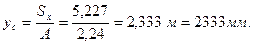
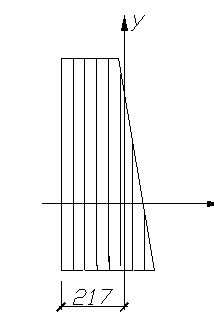
Проводим центральные оси продольного сечения колонны переменного сечения.
В соответствии с требованиями п. 7.1.4.6 [1] гибкость элементов переменного сечения, наш случай, следует определять с учётом отношения соответствующей жёсткости эквивалентного стержня к жёсткости стержня в расчётном сечении.
Жёсткость имеет выражение EI. В виду того, что модуль упругости не меняется по высоте колонны, его можно исключить. Тогда остаётся найти момент инерции эквивалентного стержня, т. е. момент инерции поперечного сечения на уровне центра тяжести продольного сечения, т. е. в опорном сечении.
Итак, высота поперечного сечения эквивалентного стержня (на расстоянии 3000 мм от опоры) определится из соотношения:
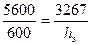, откуда hэ = 350 мм = 0,35 м.
Тогда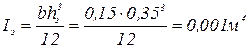 
.
Момент инерции в опорном (расчётном сечении):
.
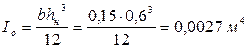Их соотношение обозначим через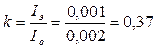 
.
Гибкость в расчётном сечении определим по формуле 7.16 [1]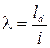 
, где i = 0,29hinf = 0,29 × 0,6 = 0,174 м.
Тогда гибкость: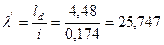 
.
Гибкость с учётом k: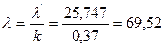 
.
На колонну действуют следующие нагрузки: продольная сила Nd, равная по величине опорной реакции фермы покрытия (Nd = 111,836 кН);
Ветровая нагрузка в виде равномерно-распределённой. Для данного района по ветровым напорам в соответствии с [2], w =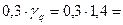 
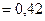кН/м2.
Для приведения ветровой нагрузки к линейно-распределённой умножаем w' на шаг колонн. Тогда w = w' × B = 0,42× 4,8 = 2,016 кН/м.
Тогда вертикальная равномерно-распределённая нагрузка на стойку от давления w + и от отсоса w - будут соответственно равны:
w + = 0,8 × w = 0,8 × 2,016 = 1,613 кН/м;
w - = 0,6 × w = 0,6× 2,016=1,21 кН/м.
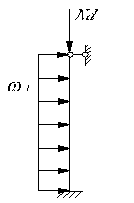Итак, расчётная схема примет вид:
Колонна является сжато-изгибаемым элементом, следовательно, в соответствии с пунктом 7.1.9.1 [1] при изгибе с осевым сжатием должно удовлетворяться следующее условие 7.31 [1]:
,
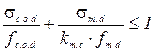где sc.o.d – определяется по формуле: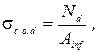 
где Ainf - площадь в расчётном сечении - Ainf = binf×hinf = 0,15 × 0,6 = 0,09 м2;
Тогда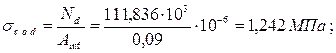 
fc.o.d - расчётное сопротивление сжатию, определяемое по таблице 6.5 с учётом требований 6.14 [1]. 
fc.o.d= fc.o.d×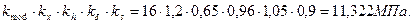 
sm.d - расчётное напряжение изгиба, определяется по формуле 7.22 [1]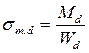 
;
где Md - расчётный изгибающий момент относительно соответствующей оси (в нашем случае y);
; 
;
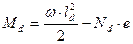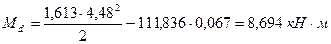Wd - расчётный момент сопротивления,
;
;
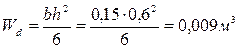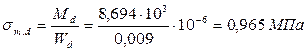km.c - коэффициент, учитывающий увеличение напряжений при изгибе по направлению соответствующей оси от действия продольной силы, определяется по формуле.
Km.c - определяется по формуле 7.32 [1]:
,
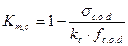где kc - коэффициент продольного изгиба, определяемый в соответствии с требованиями п. 7.1.4.2 [1].
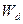- расчётный момент сопротивления верхнего пояса;
Тогда гибкость: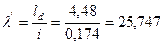 
Полученная гибкость не превышает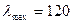 
,условие п.7.1.4.8[1].
Т.к.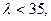 
то проводить проверку элемента на устойчивость по формуле 7.1[1] не надо:
;
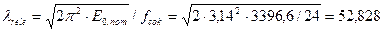где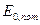 
- вероятный минимальный модуль упругости древесины вдоль волокон, определяемый по формуле 6.1[1].
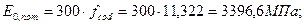
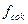- нормативное значение сопротивления древесины сжатию приложение А п.2[1].
Т.к.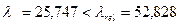 
,следовательно 
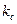-коэффициент продольного изгиба находим по формуле 7.13[1].
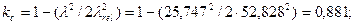
тогда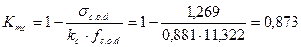 
.
Подставляя определённые составляющие в формулу 7.31[1], получим:
.
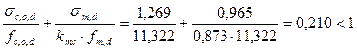Условие прочности выполняется, следовательно, запроектированная конструкция (колонна) удовлетворяет требованиям прочности.
Также согласно требованиям 7.1.9 [1] следует выполнить проверку на устойчивость плоской формы деформирования.
Расчёт на устойчивость плоской формы деформирования проводим, используя формулу 7.35 [1]:
,
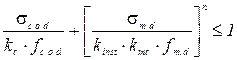где n = 2, ввиду отсутствия раскрепления растянутой кромки элемента.
kinst - коэффициент, определяемый по формуле 7.24 [1]:
;
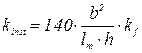lm =3м.;
kf - коэффициент, зависящий от формы эпюры изгибающих моментов на участке lm, определяемый по таблице 7.4 [1] kf = 2,54;
Тогда:
;
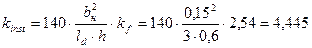После подстановки в формулу 7.35[1] численных данных получим:
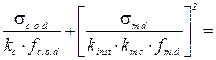
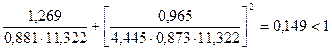
Ввиду выполнения условия 7.35 [1] приходим к выводу, что устойчивость плоской формы деформирования обеспечена при принятых размерах колонны и заданных нагрузках.