Из следующих событий укажите равновозможных события: Ответ: 1. Брошена монета. События: Герб и надпись. 5.Произведен выстрел из орудия. События: попадание и промах.
Из следующих событий укажите случайные события: Ответ: 3. Родился ребенок мужского пола 4. Стрелок попал в цель. 5. Стрелок не попал в цель
Из участков танцевального кружка, состоящего из 8 девушек и 4 юношей, выбирают 9 человек для танца. Найти вероятность того, что среди участников окажутся все юноши? Ответ: 14/55
Имеются две независимые случайные величины 
и 
. Величина распределена по нормальному закону 
. Величина распределена равномерно в интервале (0,2). Найти 
Ответ: 2
Имеются две независимые случайные величины и . Величина распределена по нормальному закону . Величина распределена равномерно в интервале (0,2). Найти 
Ответ: 1
Имеются две независимые случайные величины и . Величина распределена по нормальному закону . Величина распределена равномерно в интервале (0,2). Найти 
Ответ: 5
Интегральная функция распределения 
случайной величины определяется равенством Ответ: F(X)=P(X˂x)
Интегральная функция распределения вероятностей непрерывной величины , имеющей плотность распределения 
равна равенством Ответ: F(X)= 
Какова вероятность того, что последняя цифра наугад набранного телефонного номера окажется равной 5 или кратной 3? Ответ: 0,4
Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение одной минуты никто не позвонит Ответ: 0,37
Математическим ожиданием дискретной случайной величины , имеющей закон распределения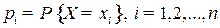 
называется число равное Ответ: M(x)= 
+ 
+…+ 
Математическим ожиданием непрерывной случайной величины с плотностью называется число равное Ответ: M(x)= 
f(x)dx
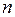Математическое ожидание биноминальной случайной величины с параметрами 
и 
равно Ответ: np
Математическое ожидание дискретной случайной величины , заданной законом распределения
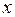
| -4 | ||
|
| 0,2 | 0,3 | 0,5 |
равно Ответ: 6
Математическое ожидание и дисперсия нормальной случайной величины с параметрами 
и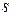 
равны Ответ: M(X)=a, D(X)= 
Математическое ожидание от произведения постоянной на случайную величину 
равно Ответ: CM(X)
Математическое ожидание отклонения от ее математического ожидания 
равно Ответ: 0
Математическое ожидание постоянной 
равно Ответ: С
Математическое ожидание произведения независимых случайных величин 
равно Ответ: M(X)*M(Y)
Математическое ожидание суммы случайных величин равно Ответ: M(X)+M(Y)
Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра случаен, то, сколько существует способов его осуществления? Ответ: 720
На 9 вакантных мест по определенной специальности претендуют 15 безработных, состоящих в службе занятости. Сколько возможно комбинаций выбора 9 из 15 безработных? Ответ: 
На железнодорожной станции имеется 5 путей. Сколькими способами можно расставить из них 3 состава? Ответ: 60
Набирая номер телефона, абонент забыл две последние цифры. Сколько номеров ему придется набрать, чтобы дозвониться, если он помнит, что эти две цифры различны. Ответ: 90
Найти вероятность того, что при перевозне 5000 изделий, хотя бы одно изделие повредится, если вероятность повреждения в пути каждого изделия равна 0,0002 Ответ: 0,63
Найти вероятность того, что событие наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом из независимых испытаниях равна 0,6. Указание j(-1,67)=0,0989 Ответ: 0,00412
Найти вероятность того, что событие наступит не менее двух раз в четырех независимых испытаниях, если вероятность наступления события в одном испытании равна 0,5 Ответ: 0,6875
Найти дисперсию дискретной случайной величины - числа появлений события 
в двух независимых испытаниях, если вероятность появления события в каждом из этих испытаний одна и та же, если известно, что математическое ожидание величины равно 1,2 Ответ: 0,48
Найти математическое ожидание 
случайной величины - число попаданий при 3-х выстрелах, если вероятность попадания при каждом выстреле р=0,4 Ответ: 1,2
Некоторое изделие, выбранное из партии готовых изделий оказалось бракованным. Укажите испытание из следующих случаев: Ответ: 5.Акт выборки
Непрерывная случайная величина распределена в интервале (0,1) по закону с плотностью 
. Найти математическое ожидание квадрата случайной величины 
Ответ: 1/2
Покупая карточку «Спортлото», игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Если при розыгрыше он угадывает все 6 чисел, то имеет шанс выиграть значительную сумму денег. Сколько существует комбинаций составить из 49 по 6, если порядок чисел безразличен? Ответ: 
Последовательность случайных величин 
называется сходящейся по вероятности к числу , если для каждого 
верно
Ответ: 
(│ 
-A│˂ ε)=1
Предполагая, что все комбинации полов детей равновероятны, определить, какую примерно долю семей с шестью детьми составляют семьи с тремя мальчиками и тремя девочками. Ответ: 5/16
Президент компании всегда приглашает одного из трех вице президентов присутствовать на бизнес - встречах и утверждает, что ее выбор кого-либо из троих - случаен. Однако один из вице президентов не был уже на трех последних встречах. Чему равна вероятность этого события, если выбор президента действительно случаен? Ответ: 8/27
Производится стрельба по мишени 
, состоящей из двух непересекающихся областей 
и 
. При этом вероятность попадания в область равна 0,5, а в область - равна 0,3. Найти вероятность попадания в область ? Ответ: 0,8
Производится стрельба по мишени , состоящей из двух пересекающихся областей и . При этом вероятность попадания в область равна 0,5, а в область - равна 0,3. Найти вероятность попадания в область ? Ответ: 0,65
Пусть - интегральная функция распределения вероятностей случайной величины . Тогда плотность распределения вероятностей определяется равенством Ответ: f(x)= 
(x)
Пусть - плотность распределения вероятностей непрерывной случайной величины . Тогда вероятность того, что значения величины попадет в промежуток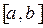 
равна Ответ: M(x)= 
F(x)dx
Пусть 
интегральная функция распределения вероятностей случайной величины , тогда вероятность того, что значение попадет в промежуток 
равна Ответ: F(β)-F(α)
Сколькими различными маршрутами можно разнести корреспонденцию в 5 адресов? Ответ:120
Сколькими способами 5 книг разных авторов можно расставить на полке в один ряд? Ответ: 120
Сколькими способами можно рассадить 5 гостей за круглым столом? Ответ: 4!
Сколько всего четырехзначных чисел можно составить из цифр Ответ: 24
Сколько существует способов составления в случайном порядке списка 7 кандидатов для выбора на руководящую должность? Ответ: 7!=5040
Сколько существует способов составления списка 20 деловых звонков случайным образом? Ответ: 21!
Случайная величина подчинена нормальному, закону 
, найти математическое ожидание случайно величины 
Ответ: M(Y)=1-3a 
Случайная величина распределена равномерно в интервале (0, а). Найти M(2X+3) Ответ: а+3
Случайная величина распределена с постоянной плотностью 
. Найти мат. ожидание случайной величины 
Ответ: M(Y)=ln2
Случайные величины и независимы. Найти дисперсию случайной величины 
, если известно, что 
Ответ: D(Z)=69
События 
образуют полную группу событий. Укажите формулу Байеса для события , которое уже произошло Ответ: P(H/A)=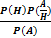 
События образуют полную группу событий. Укажите формулу полной вероятности для события Ответ: P(A)=P( 
)P(A/ )+ P( 
)P(A/ )+…. +P( 
)P(A/ )
Студент знает 20 из 30 вопросов программы. Найти вероятность того, что студент знает предложенные ему 2 вопроса? Ответ: 38/87=0,4367
Студент пришел сдавать зачет, зная из 30 вопросов только 20. Какова вероятность сдать зачет, если после отказа отвечать на первый вопрос, преподаватель задает еще один? Ответ: 26/29=0,6869
Танцевальный ансамбль, состоящий из 5 человек, выступает по 2 человека в каждом номере, пока все возможные пары танцоров не выступят. Если каждая пара танцует 5 минут без перерывов, каково общее время выступления ансамблей? Ответ: t=50мин
Танцевальный ансамбль, состоящий из N человек, выступает по R человека в каждом номере, пока все возможные пары танцоров не выступят. Если каждая пара танцует 10 минут без перерывов, каково общее время выступления ансамблей? Ответ: t= 
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадет один снаряд. Ответ: 0,092
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут два снаряда. Ответ: 0,398
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут три снаряда. Ответ: 0,504
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель не попадет ни один снаряд. Ответ: 0,006
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадет хотя бы один снаряд. Ответ: 0,994
Три орудия стреляют в цель. Вероятность попасть в цель из первого орудия равна 0,7 из второго -0,8, а из третьего -0,9. Найти вероятность того, что в цель попадут хотя бы два снаряда. Ответ: 0,902
Укажите неравенство Чебышева, если - случайная величина, ее математическое ожидание, 
- дисперсия, - число
Ответ: P(│X-M(x)│˂ ε)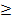 
1- 
Укажите свойство плотности распределения вероятностей
Ответ: 
f(x)dx=1
Укажите события из следующих случаев: Ответ: 3. Выпадение герб 4.Выпадение надписи
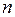Укажите формулу вероятностей для случайной величины имеющей биноминальное распределение с параметрами и , принимающей целочисленные значения от 0 до 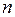. Ответ: 
Укажите формулу вероятностей для случайной величины имеющей геометрическое распределение с параметрами , принимающей целые положительные значения k=1,2,3… Ответ: p 
Укажите формулу вероятности для случайной величины имеющей распределение Пуассона с параметром 
, принимающей значения k=0,1,2…. Ответ: 
Укажите формулу вероятности появления хотя бы одного из двух зависимых событий и В Ответ: P(A+B)=P(A)+P(B) - P(A)*P(B/A)
Укажите формулу вероятности появления хотя бы одного из двух независимых событий и B Ответ: P(A+B)=P(A)+P(B)-P(A)*P(B)
Укажите формулу вероятности совместного появления двух зависимых событий и В Ответ: P(AB)=P(A)*P(B/A)
Укажите формулу вероятности совместного появления двух независимых событий и В Ответ: P(AB)=P(A)*P(B)
Укажите формулу вероятности совместного появления трех зависимых событий 
и C Ответ: P(ABC)=P(A)*P(B/A)*P(C/AB)
Укажите формулу вероятности суммы несовместных событий и B
Ответ: P(A+B)=P(A)+P(B)
Укажите формулу вероятности суммы случайных событий и В
Ответ: P(A+B)=P(A)+P(B)-P(AB)
Укажите формулу вероятности суммы случайных событий и C
Ответ: P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Укажите формулу для вычисления дисперсии случайной величины X Ответ: D(X)=M( 
) – M 
Укажите формулу для вычисления среднего квадратического отклонения случайной величины Х Ответ: 
Укажите формулу плотности распределения вероятностей нормальной случайной величины с параметрами a и s Ответ: f(x)= 
Укажите формулу плотности распределения вероятностей показательной случайной величины с параметром l Ответ: f(x)= 
Укажите формулу плотности распределения вероятностей равномерно распределенной случайной величины на [a,b]
Ответ: f(x)= 
Четырехтомное сочинение известного писателя Чингиза Айтматова расположено на полке в случайном порядке. Найти вероятность того, что тома стоят в должном порядке справа налево или слева направо. Ответ: 1/2
Число перестановок 
из элементов равно Ответ: (n)!
$$$ 233
Математическое ожидание дискретной случайной величины , заданной законом распределения
|
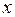
| -4 | ||
|
| 0,2 | 0,3 | 0,5 |
равно
$$$ 234
Случайная величина Х имеет закон распределения:
| Xi | ||||
| рi | 1/30 | 3/10 | 1/2 | 1/6 |
Найти её математическое ожидание
$$$ 235
Найти математическое ожидание М(Х) случайной величины Х, зная закон её распределения:
| Xi | |||
| pi | 0,2 | 0,3 | 0,5 |