Операторы и функции системы MathCAD

Операторы в системе - это команды, выраженные в виде специальных знаков, предназначенные для выполнения различных математических операций:

 

степень Х^Y Х^Y

факториал X! 4!=24

корень /X Ö9=3

абсолютное значение |x |-5|=5

нижний индекс Х[i X_i

+, -, *, / - обычным образом

суммирование членов ряда i$X åX_i

перемножение членов ряда i i#x

определенный интеграл x&f(x)

производная x?f(x)

Функции - exp(x), ln(x), log(x), cos(x) и т.д.

 

Суммирование членов ряда

i $ х i:=1.5

X_i:=2*i

åx_i=30

i

Векторными и матричными переменными в системе MathCAD, называются переменные с заданными пределами изменения.

Можно использовать другую конструкцию:

имя переменной:=N_нач, N_слу...N_кон;

шаг в этом случае равен N_слу-N_нач

 

Цикл с нецелоисчисленным изменением

 

Пример реализации двойного цикла с вложением.

i:=1..4 - внешний цикл

k:=1..3 - внутренний

a_ik:=i*k

 

 

+Система MathCAD оперирует с двумя типами массивов. Первый -одномерные массивы или векторы, второй - двумерные или матрицы.

 

 

k:=1..4 0

X: = 1

Y_k:=exp[X_k]

Y:= 2 7 1

7 3 8

20 0 8

54 59

 

Для задания вектора Alt+M, после этого может быть введено количество строк и столбцов.

Векторы обозначаются V, матрицы M, скалярные величины - буквой z.

z*v умножение вектора на скаляр

v1*v2 умножение двух векторов

m1+m2 сложение матриц

m1-m2 вычитание матриц

mⁿ возведение матрицы в n-степень

m^t транспортирование матрицы (обозначается как M[Alt]!)

Sv сумма всех элементов вектора (обозначается как Alt+$+V)

 

Система имеет так же ряд функций:

length(v) количество элементов вектора

last(v) возврашает индекс последнего элемента вектора max(v) максимальное значение

min(v) минимальное значение

rows(m) число строк матрицы

cols(m) число столбцов

tr(m) след матрицы m, сумма её диагональных элементов

 

Стандартные и пользовательские функции

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают зна­чение, скалярное или векторное (матричное). В формулах можно использовать стан­дартные встроенные функции, а также функции, определенные пользователем.

Пользовательские функции должны быть сначала определены. Определение зада­ется при помощи оператора присваивания. В левой части указывается имя пользо­вательской функции и, в скобках, формальные параметры — переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении. При использовании пользовательской функции в последующих фор­мулах ее имя вводят вручную. В диалоговом окне Insert Function (Вставка функции) оно не отображается.

Приведем обозначения основных из н y их:

1. Тригонометрические и обратные функции:

sin(z), cos(z), tan(z), asin(z), acos(z), atan(z)

z - угол в радианах

2. Гиперболические и обратные функции:

sinh(z), cosh(z), tanh(z), asinh(z), acosh(z), atanh(z)

3. Экспоненциальные и логарифмические:

exp(z) - e^z

ln(z) - натуральный логарифм

log(z) - десятичный логарифм

4. Cтатистические функции:

mean(x) - среднее значение

var(x) - дисперсия

stdev(x) - среднеквадратическое отклонение

cnorm(x)- функция нормального рапределения

erf(x) - функция ошибки

Г(x) - гамма-функция Эйлера

5. Функции Бесселя:

J0(x), J1(x), Jn(n,x) - функции Бесселя первого порядка

Y0(x), Y1(x), Yn(n,x) - функции Бесселя второго порядка

6. Функции комплексного переменного:

Re(z) - вещественная часть комплексного числа

Im(z) - мнимая часть комплексного числа

arg(z) - аргумент комплексного числа

7. Преобразование Фурье:

U:=fft(V) - прямое преобразование (V- вещественное)

V:=ifft(U) - обратное преобразование (V- вещественное)

U:=cfft(V) - прямое преобразование (V- комплексное)

V:=icfft(U) - обратное преобразование (V- комплексное)

8. Корреляционная функция - позволяет рассчитывать коэффициент корреляции двух векторов vx и vy и определить уравнение линейной регрессии:

corr(vx,vy) - коэффициент корреляции

slope(vx,vy) - коэффициент наклона линии регрессии

intercept(vx,vy) - начальная координата линии регрессии

9. Линейная интерполяция:

linterp(vx,vy,x)

vx,vy- векторы значений аргумента и функций. x- значение аргумента,

для которого проводится интерполяция

10.Функция для определения корней алгебраических и трансцендентных уравнений:

root(уравнения, переменная) - значение переменной, когда уравнение равно нулю

11.Датчик случайных чисел:

rnd(x) - случайное число с равномерным распределением от 0 до x

12.Целая часть переменной:

floor(x)- ближайшее наименьшее целое число

ceil(x)- ближайшее наибольшее целое число

13.Выделение остатка:

mod(x,y)- остаток от деления x на y

14.Остановка итерации:

until(x,y) - когда x<0

15.Функция условного перехода:

if(условие,x,y) - если условие выполняется, то функция равняется x, иначе y

16.Единичная функция (функция Хевисайда):

Ф(x) - если x>0. То функция равна 1, иначе 0

17.Логические выражения и операции. Простейшими видами логических выражений являются следующие: логическая константа, логическая константа, логическая константа, логическая переменная, выражение отношения. Например, при x:=0.5 операции отношения присваивают L истину или ложь (1 или 0):

L:= x£1 L=0

L:= x³1 L=0

L:= x»1 L=0

L:= x<1 L=1

L:= x>1 L=0

18.Функции, определяемые пользователем. Пользователь может самостоятельно определить необходимые ему функции, отсутствующие среди встроенных функций пакета.

 

Ввод текста

Текст, помещенный в рабочий лист, содержит комментарии и описания и предназна­чен для ознакомления, а не для использования в расчетах. Программа MathCad опре­деляет назначение текущего блока автоматически при первом нажатии клавиши ПРОБЕЛ. Если введенный текст не может быть интерпретирован как формула, блок преобразуется в текстовый и последующие данные рассматриваются как текст. Создать текстовый блок без использования автоматических средств позволяет команда Insert > Text Region (Вставка > Текстовый блок).

Иногда требуется встроить формулу внутрь текстового блока. Для этого служит команда Insert > Math Region (Вставка > Формула).

 

Решение уравнений и систем

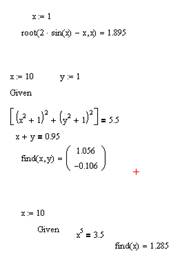Для численного поиска корней уравнения в программе MathCad используется функция root. Она служит для решения уравнений вида f(x) = 0, где f (х) — выражение, корни которого нужно найти, a x — неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: r oot (f(x),x). Здесь f(x) — функция перемен­ной х, используемой в качестве второго параметра. Функция root возвращает зна­чение независимой переменной, обращающее функцию f(x) в 0. Например:

 

Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения. Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом функции find (найти). Между ними располагают «логические утверждения», задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения.

Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства — кнопка Boolean Equals (Логически равно) на панели инструментов Evaluation (Вычисление). Другие знаки логических условий также можно найти на этой панели. Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечислены искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных.

Построение графиков

Чтобы построить двумерный график в координатных осях Х-У, надо дать команду

Insert> Graph > X-Y Plot (Вставка > График > Декартовы координаты). В области раз­мещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназна­чен для переменной или выражения, отображаемого по этой оси. Обычно используют диапазон или вектор значений. Граничные значения по осям выбираются автома­тически в соответствии с диапазоном изменения величины, но их можно задать и вручную. В одной графической области можно построить несколько графиков.

Аналитические вычисления

С помощью аналитических вычислений находят аналитические или полные реше­ния уравнений и систем, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить нечисло­вой результат. В программе MathCad конкретные значения, присвоенные переменным, при этом

игнорируются — переменные рассматриваются как неопределенные пара­метры. Команды для выполнения аналитических вычислений в основном сосредо­точены в меню Symbolics (Аналитические вычисления). Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Symbolics > Simplify (Аналитические вычисления > Упростить). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тож­дества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции (типа e^Inx ). Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения коман­ды Symbolics > Expand (Аналитические вычисления > Раскрыть). Команду Symbolics > Simplify (Аналитические вычисления > Упростить) применяют и в более сложных случаях. Например, с ее помощью можно:

• вычислить предел числовой последовательности, заданной общим членом;
• найти общую формулу для суммы членов числовой последовательности, задан­ной общим членом;
• вычислить производную данной функции;
• найти первообразную данной функции или значение определенного интеграла.

Другие возможности меню Symbolics (Аналитические вычисления) состоят в выполне­нии аналитических операций, ориентированных на переменную, использованную в выражении. Для этого надо выделить в выражении переменную и выбрать команду из меню Symbolics> Variable (Аналитические вычисления > Переменная). Команда Solve (Решить) ищет корни функции, заданной данным выражением, например, если выде­лить уголковым курсором переменную х в выражении ах² + bx + с, то в результате применения команды Symbolics > Variable > Solve (Аналитические вычисления > Пере­менная > Решить), будут найдены все корни:

 

Другие возможности использования этого меню включают:

• аналитическое дифференцирование и интегрирование: Symbolics > Variable > Differentiate (Аналитические вычисления > Переменная > Дифференцировать) и Symbolics > Variable > Integrate (Аналитические вычисления > Переменная > Интегри­ровать);
• замена переменной: Symbolics > Variable > Substitute (Аналитические вычисления > Переменная > Подставить) — вместо переменной подставляется содержимое буфера обмена;
• разложение в ряд Тейлора: Symbolics > Variable > Expand to Series (Аналитические вычисления > Переменная > Разложить в ряд),
• представление дробно-рациональной функции в виде суммы простых дробей с линейными и квадратичными знаменателями: Symbolics > Variable > Convert to Partial Fraction (Аналитические вычисления > Переменная > Преобразовать в про­стые дроби).

Наконец, самым мощным инструментом аналитических вычислений является опе­ратор аналитического вычисления, который вводится с помощью кнопки Symbolic Evaluation (Вычислить аналитически) на панели инструментов Evaluation (Вычисление). Его можно, например, использовать для аналитического решения системы уравнений и неравенств. Блок решения задается точно так же, как при численном решении (хотя начальные значения переменных можно не задавать), а последняя формула блока должна выглядеть

find(x,y,...)®, где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо. Любое аналитическое вычисление можно применить с помощью ключевого слова. Для этого используют кнопку Symbolic Keyword Evaluation (Вычисление с ключевым словом) на панели инструментов Evaluation (Вычисление). Ключевые слова вводятся через панель инструментов Symbolics (Аналитические вычисления). Они полностью охватывают возможности, заключенные в меню Symbolics (Аналитические вычис­ления), позволяя также задавать дополнительные параметры.

Программирование

Наиболее заметная «изюминка» MathCAD, которую сразу оценили пользователи, - это встроенный язык программирования. В MathCAD, по сути, не встроен язык программирования, а просто снято ограничение на использование составных операторов в теле алгоритмических управляющих конструкций выбор и повторение. Кроме того, добавлены цикл с параметром и оператор досрочного выхода break. Алгоритмические конструкции и составные операторы в среде MathCAD вводятся нажимом одной из семи кнопок панели управления:

Add line
if	while
for	break
otherwise

Add line - добавить строку программы, тела цикла, плеча альтернативы и т.д.

- знак присвоения.

While - при нажатии на эту кнопку на экране появляется заготовка цикла с предпроверкой: слово while с двумя пустыми квадратиками. В квадратик правее while нужно записать булево выражение (переменную), управляющее циклом, а во второй квадратик (ниже while) - тело цикла.

If - позволяет вводить в программу альтернативу с одним плечом.

Otherwise - позволяет превратить неполную альтернативу в полную:

C D if A > B

E F otherwise

for - кнопка для ввода в программы цикла с параметром.

Break - кнопка досрочного выхода из программы или цикла.