Перевод целых чисел
Алгоритм перевода. Пусть  - десятичное целое число. Тогда в расположении отсутствуют коэффициенты с отрицательными индексами. Данное число представляется в виде:
- десятичное целое число. Тогда в расположении отсутствуют коэффициенты с отрицательными индексами. Данное число представляется в виде:

1. Число  разделим на q. Неполное частное равно:
разделим на q. Неполное частное равно:

2. Полученное неполное частное опять делим на q, остаток отделения равен  .
.
3. Продолжаем данный процесс деления, пока на n-м шаге не получим набор цифр: которые входят в q – ичное представление числа  и совпадают с остатками при последовательном делении данного числа на q.
и совпадают с остатками при последовательном делении данного числа на q.
4. Запишем десятичное число в новой системе счисления, начиная запись с последнего частного:

Пример 1. Переведите число  в двоичную, восьмеричную и шестнадцатеричную системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления  .
.
| _123 | ||||||
| _61 | ||||||
| _30 | ||||||
| _15 | ||||||
| _7 | ||||||
| _3 | ||||||
 Результат 1:
Результат 1: 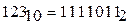
Проверка 1: 
| _123 | ||
| _15 | ||
 3 3
| ||
Результат 2: 
Проверка 2: 
| _123 | |
Результат 3: 
Проверка 3: 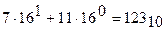
Перевод дробных чисел
Алгоритм перевода. Пусть  - правильная десятичная дробь. Тогда в разложении отсутствуют коэффициенты с положительными индексами. Данное число представим в виде:
- правильная десятичная дробь. Тогда в разложении отсутствуют коэффициенты с положительными индексами. Данное число представим в виде:
 (6)
(6)
- Для нахождения коэффициентов
 входящих в запись числа в q –ичной системе счисления, умножим левую и правую части выражения (6) на q. В результате в правой части получим
входящих в запись числа в q –ичной системе счисления, умножим левую и правую части выражения (6) на q. В результате в правой части получим  . Целая часть равна
. Целая часть равна  , является старшим коэффициентом в разложении числа
, является старшим коэффициентом в разложении числа  по степеням q.
по степеням q. - Оставшуюся дробную часть умножим на q:
 , где цифра
, где цифра  представляет собой второй коэффициент после запятой q- ичном представлении исходного числа.
представляет собой второй коэффициент после запятой q- ичном представлении исходного числа. - Продолжаем перемножение дробной части на q до тех пор, пока в правой части не получим нуль или не будет достигнута необходимая точность вычислений.
Пример 2. Переведите десятичную дробь 0,5625 в двоичную систему исчисления.
| 0, |

|

| |

| |

| |
Результат:  .
.
Пример 3. Переведите десятичную дробь 0,65625 в восьмеричную и шестнадцатеричную системы исчисления.
Результат:
|
Результат:
|
Пример 4. Переведите десятичную дробь 0,7 в восьмеричную систему исчисления.
| 0, |

|

| |

| |

| |
| ……. |
Даны процесс может продолжаться бесконечно. Такой бесконечный процесс завершается на некотором шаге, когда считается, что получена требуемая точность представления числа.
Пример 5. Переведите десятичную дробь 0,101 в двоичную систему исчисления. В двоичной записи сохраните четыре знака.
| 0, |

|

| |

| |

| |
| ……. |
Результат:  .
.
Перевод смешанных чисел
Перевод смешанных чисел, содержащих целую и дробные части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся согласно приведенным выше алгоритмам. В итоговой записи в новой системе счисления целая часть отделяется от дробной запятой или точкой.
Пример 6. Переведите число 12,25 в двоичную систему счисления.
Переведем целую часть:
| _12 | |||
| _6 | |||
 0 0
| _3 | ||
Переведем дробную часть:
| 0, |

|

| |
Результат:  .
.
Арифметические операции в позиционных системах счисления
Рассмотрим арифметические операции на примере двоичной системы счисления. Рассмотрим таблицы сложения, вычитания и умножения.
Сложение в двоичной системе счисления
0+0=0
0+1=1
1+0=1
1+1=10
Примеры. Выполните операцию сложения над двоичными числами:
| + | + | + | ||
 .
.
 .
.