В различных разделах математики рассматриваются последовательности вида: (x 1, x 2), (x 1, x 2, x 3), …, (x 1, x 2, x 3, …, xn). Такие последовательности называют двух-, трех-, …, n- мерными векторами, а числа x 1, x 2, x 3, …, xn - координатами векторов В дискретной математике часто используются двоичные векторы или векторы над полем В ={0,1}. Координатами таких векторов служат числа 0 или 1. Фактически, n -мерный двоичный вектор – это последовательность из n нулей и единиц.
Двоичные векторы можно покоординатно складывать, находить их скалярное произведение, используя при этом следующие таблицы:
| Å | ´ | |||||
Операции «Å» и «´» называют сложением и умножением по модулю два соответственно
Пример. Даны векторы 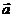 =(0,1,1,0,1),
=(0,1,1,0,1), 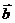 =(1,0,1,1,1) над полем В ={0,1}. Найти
=(1,0,1,1,1) над полем В ={0,1}. Найти 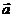 Å
Å 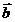 и скалярное произведение
и скалярное произведение 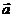 ×
× 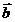 .
.
Р е ш е н и е.
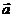 Å
Å 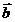 =(0Å1,1Å0,1Å1,0Å1,1Å1)=(1,1,0,1,0).
=(0Å1,1Å0,1Å1,0Å1,1Å1)=(1,1,0,1,0).
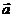 ×
× 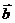 =0×1Å1×0Å1×1Å0×1Å1×1=0
=0×1Å1×0Å1×1Å0×1Å1×1=0 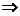
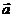 и
и 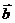 ортогональны.
ортогональны.
Переменные, принимающие значения на двухэлементном множестве, называют булевыми переменными: 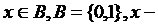 булева переменная.
булева переменная.
В различных технических устройствах используются логические элементы: конъюнкторы, дизъюнкторы, инверторы и др. Основная цель использования схем логических элементов – преобразование информации, подаваемой на входы схемы.
Инвертор – устройство с одним входом и одним выходом, преобразующее входной сигнал x в выходной сигнал 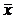 по правилу, указанному в таблице истинности отрицания (рис.1).
по правилу, указанному в таблице истинности отрицания (рис.1).

Переход от x к 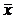 можно рассматривать как унарную (одноместную) операцию на множестве булевых переменных. Операцию эту называют отрицанием, символ
можно рассматривать как унарную (одноместную) операцию на множестве булевых переменных. Операцию эту называют отрицанием, символ 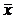 читают “НЕ x ”. Операция отрицания обладает очевидным свойством, которое называют законом отрицания отрицания:
читают “НЕ x ”. Операция отрицания обладает очевидным свойством, которое называют законом отрицания отрицания:
 (отрицание отрицания x есть x).
(отрицание отрицания x есть x).
Конъюнктор – устройство с двумя входами x 1 и x 2 и одним выходом y = x 1 ^ x 2 (рис. 2, а).

Правило преобразования сигналов x 1, x 2 в сигнал y записано в таблице истинности конъюнкции (рис. 13, б). С точки зрения математики конъюнктор выполняет бинарную (двуместную) операцию на множестве булевых переменных, которую называют коньюнкцией. Знак конъюнкции “^” (или “&”) читают как “И”: x 1^ x 2 – x 1 И x 2.
Укажем свойства конъюнкции:
| 1. x 1^ x 2= x 2^ x 1 | - коммутативность |
| 2. (x 1^ x 2) ^ x 3= x 1^(x 2 ^ x 3) | - ассоциативность |
| 3. x = x ^ x | - идемпотентность |
| 4. x ^0=0^ x =0 | - свойство 0 |
| 5. x ^1=1^ x = x | - свойство 1. |
Дизъюнктор – устройство, реализующее бинарную операцию дизъюнкция на множестве булевых переменных, определенную таблицей истинности дизъюнкции (рис. 3).
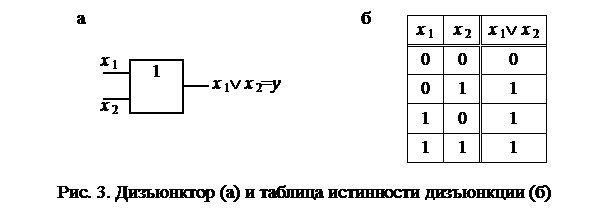
Знак дизъюнкции “Ú” читают “ИЛИ”: x 1Ú x 2 – x 1 ИЛИ x 2.
Свойства дизъюнкции:
| 1. x 1Ú x 2= x 2Ú x 1; | – коммутативность |
| 2. (x 1Ú x 2) Ú x 3= x 1Ú(x 2Ú x 3); | – ассоциативность |
| 3. x Ú x = x; | – идемпотентность |
| 4. x Ú0= x; | – свойство 0 |
| 5. x Ú1=1. | – свойство 1 |
Операции ¯, Ù, Ú связаны друг с другом следующими равенствами:

Помимо конъюнктора, дизъюнктора и инвертора в логических схемах довольно часто используется устройство, называемое одноразрядным двоичным сумматором, и реализующее сложение по модулю 2 (рис. 4)

Свойства операции сложения по модулю 2
1. x 1  x 2= x 2 x 2= x 2  x 1; x 1;
| – коммутативность |
2. (x 1  x 2) x 2)  x 3= x 1 x 3= x 1  (x 2 (x 2  x 3); x 3);
| – ассоциативность |
3. x  x =0; x =0;
| |
4. x  0= x; 0= x;
| – свойство 0 |
5. x  1= 1= 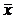 . .
| – свойство 1 |
Операция  связана с операциями ¯, Ù, Ú следующими равенствами:
связана с операциями ¯, Ù, Ú следующими равенствами:
1. x 1Ù(x 2  x 3)=(x 1Ù x 2) x 3)=(x 1Ù x 2)  (x 1Ù x 3) (x 1Ù x 3)
| – дистрибутивность конъюнкции относительно сложения |
2. x 1Ú x 2= x 1  x 2 x 2  (x 1Ù x 2); (x 1Ù x 2);
| – выражение дизъюнкции через сложение по модулю 2 |
3. x 1  x 2=( x 2=(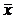 1Ú x 2 ) Ù(x 1Ú 1Ú x 2 ) Ù(x 1Ú 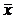 2) 2)
| – выражение сложение по модулю 2 через дизъюнкции |
При выполнении преобразований выражений с булевыми переменными принят следующий порядок выполнения операций:
1. Первой выполняется операция отрицания отдельной булевой переменной.
2. При наличии скобок сначала выполняются действия в скобках.
3. При отсутствии скобок сначала выполняется конъюнкция, а затем по порядку дизъюнкция и сложение.
Обратим внимание на то, то конъюнкция по своим свойствам относительно дизъюнкции и сложения аналогична операции умножения чисел. Поэтому знак конъюнкции «Ù» в выражения с булевыми переменными часто опускается, аналогично тому, как опускается знак умножения в числовых выражениях.
Примеры:
1. (x 1Ù x 2)  (x 1Ù x 3) = x 1 x 2
(x 1Ù x 3) = x 1 x 2  x 1 x 3;
x 1 x 3;
2. (x 1Ù x 2) Ú (x 1Ù x 3) = x 1 x 2Ú x 1 x 3.