Изучение нового материала.
Законы Кеплера.
В формировании представлений о строении Солнечной системы важную роль сыграли законы движения планет, открытые австрийским астрономом Иоганном Кеплером.
Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы. Кеплеру надо было построить орбиты планет, перейти от экваториальной системы координат к системе, указывающей её положение в плоскости орбиты.
. 1ыйзакон Кеплера. (открыт в 1605 году, напечатан в 1609г в книге “Новая астрономия” вместе с 2-м законом).
Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.
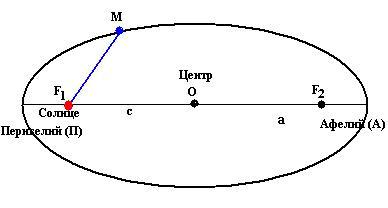
Для построения орбиты планет (на примере Марса) Кеплер, перейдя от экваториальной системы координат
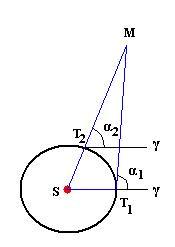
к системе координат, указывающих его положение в плоскости орбиты, принял в приближении орбиту Земли окружностью. Для построения орбиты применил способ, показанный на рисунке, отсчитывая прямое восхождение от точки весеннего равноденствия на положение нескольких противостояний Марса. Проведя по полученным точкам плавную кривую получил эллипс и нашел формулу описывающую орбиту планеты X=е*sin(а)+M
Эллипс - замкнутая кривая, у которой сумма расстояний от любой точки до фокусов постоянна.
Эллипс характеризуется
эксцентриситетом (степень сжатия-отличие от окружности-) :
е=с/а,
где а - большая полуось орбиты,
а с - расстояние от центра эллипса до его фокуса.
При е=с=0 эллипс превращается в окружность, а при е=1 в отрезок.
Для эллиптической орбиты планеты характерны точки:
Перигелий (греч.пери–возле,около)ближайшая к Солнцу точкаорбиты планеты (для Земли 1-5 января).
Афелий (греч.апо–вдали)наиболее удаленная от Солнца точкаорбиты планеты (для Земли 1-6 июля).
Большая полуось орбиты Земли (среднее расстояние Земли от Солнца) называется астрономической единицей.
1а.е.=149 597 868 ± 0,7 км ≈ 149,6 млн. км.
2ойзакон Кеплера. (открыт в1601году,напечатан в1609г в книге“Новаяастрономия” вместе с 1-м законом).
Радиус-вектор планеты за равные промежутки времени описывает равные площади.
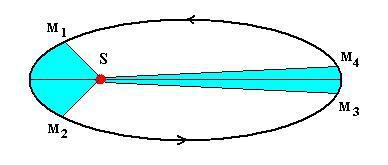
2 закон называют законом площадей.
Заштрихованные площади фигур равны.
Из чертежа видно, что дуги (пройденные пути) разные,
отсюда υп>υа, т.е в перигелии υmax, а в афелии υmin.
По закону сохранения энергии полная механическая энергия замкнутой системы, между которыми действует сила тяготения, остается неизменной при любых движениях тел этой системы.
Поэтому сумма кинетической и потенциальной энергии планеты неизменна во всех точках орбиты.
По мере приближения к Солнцу кинетическая энергия планеты возрастает, а ее потенциальная энергии уменьшается.
3ийзакон Кеплера. (открыт в1618году,напечатан в1619г в книге“Гармония мира”).
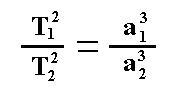
Квадраты звездных (сидерических) периодов обращения планет
относятся между собой как кубы больших полуосей их орбит.
Этот закон позволил впервые решить задачу движения 2х тел, тогда как
первые 2 рассматривают движение планет в отдельности.
10). Границы применимости законов Кеплера:
· применимы для описания движения планет, но не объясняют причин движения;
· позволяют вычислить относительные расстояния планет от Солнца;
· применимы не только к движению планет, но и их естественных
спутников, других небесных тел (астероидов, комет, звёзд в двойных системах).
2). Значение законов Кеплера:
· подтвердили гелиоцентрическую систему устройства мира Коперника;
· преодолели заключения о круговых движениях небесных тел с опорой
· на эмпирические данные;
· ввели понятие астрономической единицы;
· явились опорой для открытия других законов (закон Тициуса-Боде).
3. Закрепление материала.
Задача 1. “Спутник-1”, запущенный 4 октября 1957г на орбиту Земли имел перигей 228 км и апогей 947 км при периоде обращения 96,2 мин. Определите большую полуось и эксцентриситет орбиты.
Решение:
а= (ап+R+R+аа)/2=
= (228+ 6371+6371+947)/2=
=6958,5 км
е=с/а
[c= (аа - ап)/2-
получим е= 0,052, а1/а2=2)
Домашнее задание:
1. Разобрать задачу
2. Заполнить таблицу

| Формулировка | Графическая интерпретация |
Закона
Первый закон
Второй закон
(площадей)
Третий закон
Граница
Применимости