Моментом силы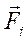 
относительно неподвижной точки О (полюса) называется векторная величина 
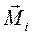, равная векторному произведению
, где
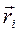– радиус-вектор, проведённый из точки О в точку А приложения силы.
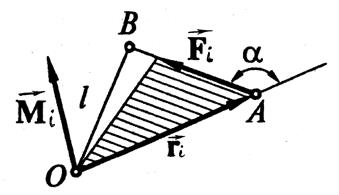
По модулю момент силы равен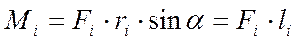 
, где
– плечо силы 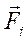– кратчайшее расстояниеот точки О до линии действия силы.
Главным моментом (результирующим) системы сил относительно точки О называется вектор 
, равный векторной сумме моментов относительно точки О всех сил системы
.
Моментом импульса (моментом количества движения) материальной точки относительно неподвижной точки О (полюса) называют вектор
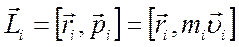, где
тi и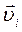 
– масса и скорость материальной точки.
Моментом импульса системы относительно неподвижной точки О называют векторную сумму моментов импульса относительно той же точки О всех материальных точек системы:
.
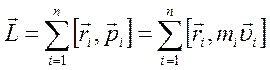
Если твёрдое тело вращается с угловой скоростью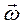 
вокруг точки О, то момент импульса тела относительно неподвижной точки О
. где
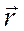– радиус-вектор, проведённый из точки О в малый элемент тела массой dm;
– скорость этого элемента тела.
Поскольку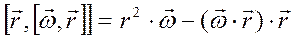 
– векторы 
и 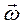в общем случае не совпадают по направлению
.
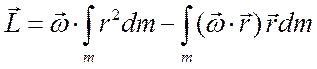Моментом инерции механической системы относительно неподвижной оси 
OZ называется физическая величина JZ, равная
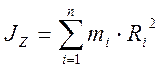, где
mi и Ri – масса i –й точки и её расстояние от оси OZ.
Момент инерции твёрдого тела относительно неподвижной оси OZ
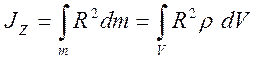, где
dm = ρ.dV – масса малого элемента тела объёмом dV;
ρ – плотность материала твёрдого тела;
R – расстояние от элемента dV до оси OZ.
Если тело однородно, т.е. его плотность всюду одинакова, то
.
Момент инерции тела JZ является мерой инертности тела во вращательном движении вокруг неподвижной оси OZ подобно тому как масса тела является мерой его инертности в поступательном движении.
Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.
Согласно теореме Штейнера момент инерции тела JO относительно произвольной оси О равен сумме момента инерции тела JС относительно оси С, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела т на квадрат расстояния а между осями
JO = JC + m.а 2.
Доказательство теоремы:
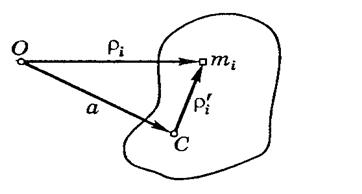
Пусть положение i -го элемента твёрдого тела относительно осей О и С характеризуется векторам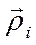и 
и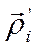 
, а положение оси С относительно оси О – вектором 
, плоскость которого перпендикулярна осям О и С. Воспользовавшись связью между этими векторами 
, преобразуем выражение для момента инерции тела относительно оси О следующим образом:
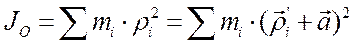, или
.
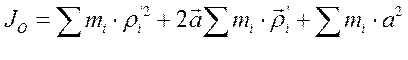В правой части этого равенства первая сумма представляет собой момент инерции тела JC i -го элемента твёрдого тела относительно оси С, а последняя сумма равна m.а 2. Покажем, что средняя сумма равна нулю.
Пусть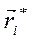 
– радиус-вектор i -го элемента твёрдого тела относительно центра масс, тогда относительно центра масс суммарный вектор 
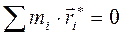. Но 
– это составляющая вектора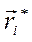 
, перпендикулярная осям О и С. Очевидно, что если суммарный вектор равен нулю, то сумма его составляющих в плоскости, перпендикулярной осям О и С, также равна нулю, т.е. 
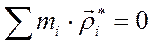и теорема доказана.
Моменты инерции некоторых однородных твёрдых тел:
| Тело | Положение оси | Момент инерции |
| Обруч или полый тонкостенный цилиндр радиуса R и массы т | Ось обруча или цилиндра | mR2 |
| Сплошной цилиндр или диск радиуса R и массы т | Ось цилиндра или диска |
|
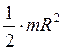
| Шар радиуса R и массы т | Ось проходит через центр шара |
|
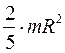
| Тонкостенная сфера радиуса R и массы т | Ось проходит через центр сферы |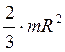 
|
| Прямой тонкий стержень длины l и массы т | Ось перпендикулярна к стержню и проходит через его середину Ось перпендикулярна к стержню и проходит через его конец |
|
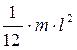
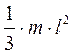