Пусть материальная точка совершает прямые гармонические колебания вдоль оси ОХ
, тогда
и
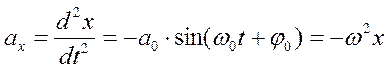, где
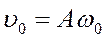– амплитуда скорости;
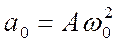– амплитуда ускорения.
По второму закону Ньютона сила, действующая на материальную точку
.
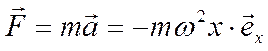Такая зависимость силы от смещения характерна для упругой силы.
Силы иной физической природы, удовлетворяющие тому же виду зависимости, называются квазиупругими.
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
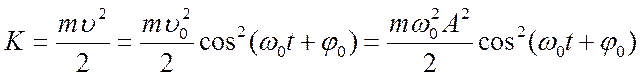или
.
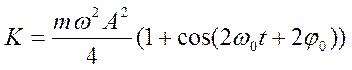Кинетическая энергия К изменяется от 0 до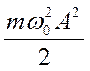 
, совершая гармонические колебания с частотой 2 ω 0 и амплитудой 
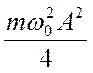около среднего значения, равного 
.
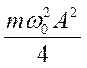Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы, равна
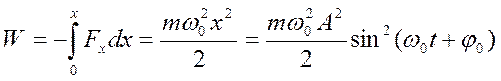или
.
Таким образом, потенциальная энергия W периодически изменяется от 0 до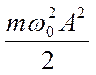 
, совершая гармонические колебания с циклической частотой 2 ω 0 и амплитудой 
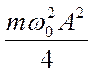около среднего значения, равного 
.
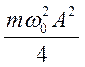Колебания потенциальной и кинетической энергии совершаются со сдвигом по фазе на π, так что полная механическая энергия материальной точки не изменяется при гармонических колебаниях:
E, K, W
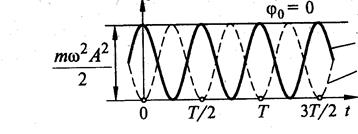E
K
W
Линейный гармонический осциллятор –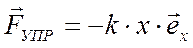 
(например, пружинный маятник).
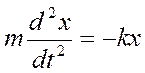или 
Это уравнение является дифференциальным уравнением гармонических колебаний, решением которого является
,
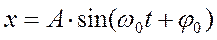где 
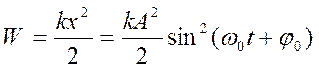
Импульс гармонического осциллятора
.
Если из системы уравнений р (t) и x (t) исключить время то после преобразований приходим к уравнению, которое на координатной плоскости х, р ( фазовой плоскости ) является уравнением эллипса
.
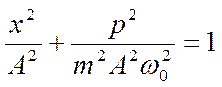График зависимости р = р (х) называют фазовой траекторией. Любая точка этой траектории соответствует состоянию осциллятора в некоторый момент времени. Ниже представлены фазовые траектории свободных незатухающих колебаний, образующих семейство подобных эллипсов (отношение длин полуосей равно k 2).
Каждому эллипсу соответствует определённый уровень энергии осциллятора. Площадь эллипса равна произведению его полуосей, умноженному на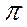 
:
.
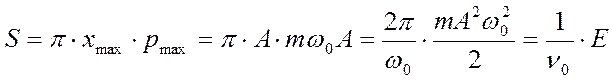Следовательно, для полной энергии осциллятора можно записать 
,
где интеграл представляет из себя площадь, охватываемую фазовой кривой.
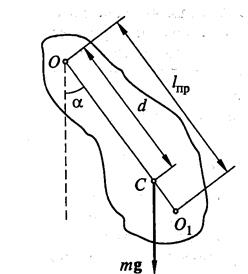Физический маятник – твёрдое тело, которое может вращаться под действием своей силы тяжести mg вокруг неподвижной горизонтальной оси О, не проходящей через центр масс тела и называемой осью качания маятника.
Если пренебречь силами трения в подвесе маятника, то момент относительно оси качания создаёт только mg и при отклонении маятника на угол α эта сила создаёт момент численно равный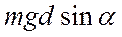 
и стремящийся возвратить маятник в положение равновесия (α = 0).
В соответствии с основным законом динамики твёрдого тела, вращающегося вокруг неподвижной оси, уравнение движения физического маятника имеет вид
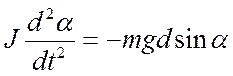, где
– расстояние от центра масс маятника до оси качания;
J – момент инерции маятника относительно той же оси.
При малых колебаниях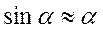 
. Тогда
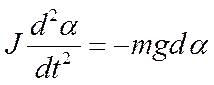и угол α удовлетворяет дифференциальному уравнению гармонических колебаний
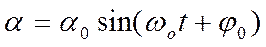, где
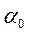– амплитуда колебаний угла 
.
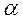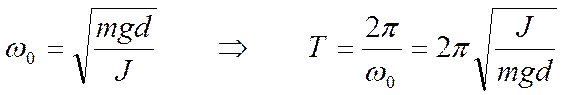
Математический маятник – предельный случай физического маятника – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
В этом случае d = l – длина математического маятника, а J = ml 2.
Соответственно 
.
Длина математического маятника, имеющего такой же период колебаний, что и данный физический маятник называется приведённой длиной l пр этого физического маятника
.
Точка О1, лежащая на прямой ОС на расстоянии l пр от точки подвеса О, называется центром качания физического маятника. Точки О и О1 обладают свойством взаимности.
Лекция 6