Одновременность событий в разных системах отсчёта
Пусть в системе К в точках х 1 и х 2 происходят одновременно два события в момент времени t 1 = t 2 = τ. Тогда в системе К’ этим событиям будут соответствовать моменты
 и
и  т.е.
т.е.
если в К-системе события пространственно разобщены, то в К’-системе они не будут одновременными  .
.
Это означает, что в одних системах событие 1 будет предшествовать событию 2, а в других системах может быть наоборот. Сказанное относится лишь к событиям, между которыми отсутствует причинная связь. (Рождение элементарной частицы во всех системах отсчёта происходит раньше её распада и ни в одной из систем ребёнок не рождается раньше его родителей).
Длина тел в разных системах
 Рассмотрим стержень, расположенный вдоль оси ОХ’ и покоящийся относительно К’-системы.
Рассмотрим стержень, расположенный вдоль оси ОХ’ и покоящийся относительно К’-системы.
Длина его в этой системе
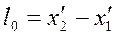 .
.
Относительно К-системы стержень движется со скоростью 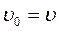 . Для определения его длины в этой К-системе нужно отметить координаты его концов х 1 и х 2 в один и тот же момент времени τ = t 1= t 2 .
. Для определения его длины в этой К-системе нужно отметить координаты его концов х 1 и х 2 в один и тот же момент времени τ = t 1= t 2 .
Из преобразований Лоренца получаем
 и
и 
откуда  или
или 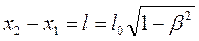 .
.
Таким образом, длина стержня l, измеренная в системе, относительно которой он движется, оказывается меньше длины l 0, измеренной в системе, относительно которой стержень покоится.
В направлении осей ОУ и OZ размеры стержня одинаковы во всех системах отсчёта.
Промежуток времени между событиями
Пусть в одной и той же точке А системы К* происходят два события в моменты времени  и
и 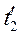 . Полагая
. Полагая  получим
получим
 и
и 
Тогда  или
или
 , где
, где
 – собственное время тела, неподвижного относительно К’-системы и движущегося со скоростью
– собственное время тела, неподвижного относительно К’-системы и движущегося со скоростью 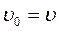 относительно К-системы (т.е. промежуток времени, измеренный по часам, неподвижным относительно движущегося тела т.е., движущимся вместе с телом).
относительно К-системы (т.е. промежуток времени, измеренный по часам, неподвижным относительно движущегося тела т.е., движущимся вместе с телом).
 – инвариант. В какой бы системе отсчёта ни рассматривалось движение тела, промежуток собственного времни измеряется по часам системы, в которой частица покоится. Отсюда следует, что промежуток собственного времени является инвариантом, т.е. величиной, имеющей одно и то же значение во всех инерциальных системах отсчёта.
– инвариант. В какой бы системе отсчёта ни рассматривалось движение тела, промежуток собственного времни измеряется по часам системы, в которой частица покоится. Отсюда следует, что промежуток собственного времени является инвариантом, т.е. величиной, имеющей одно и то же значение во всех инерциальных системах отсчёта.
Собственное время всегда меньше, чем время, отсчитанное по часам, движущимся относительно тела (движущиеся часы идут медленнее, чем покоящиеся часы).
Это явление получило непосредственное экспериментальное подтверждение в опытах с мюонами.
Мюон – нестабильная элементарная частица, распадающаяся на электрон (или позитрон) и два нейтрино и имеющая среднее собственное время жизни в условиях, когда они движутся с малой скоростью  мкс. Мюоны рождаются в верхних слоях атмосферы под действием первичных космических лучей и движутся к Земле со скоростями υ ~ c. Если бы релятивистского эффекта замедления хода времени не было, то по отношению к земному наблюдателю мюон мог бы пройти за время своей жизни путь в атмосфере, не превосходящий в среднем
мкс. Мюоны рождаются в верхних слоях атмосферы под действием первичных космических лучей и движутся к Земле со скоростями υ ~ c. Если бы релятивистского эффекта замедления хода времени не было, то по отношению к земному наблюдателю мюон мог бы пройти за время своей жизни путь в атмосфере, не превосходящий в среднем  м. Но они регистрируются приборами, установленными на поверхности Земли, т.е., время жизни мюона по часам земного наблюдателя
м. Но они регистрируются приборами, установленными на поверхности Земли, т.е., время жизни мюона по часам земного наблюдателя  .
.
Парадокс часов
Согласно принципу относительности, все процессы на космическом корабле, движущемся относительно Земли, включая и процесс старения космонавтов, идут по тем же законам, что и на Земле. Но если космонавт, совершив космический полёт со скоростью близкой к скорости света возвратится на Землю, то он может оказаться среди представителей последующих поколений (полёт в будущее).
На первый взгляд кажется, что основываясь на принципе относительности, можно прийти к прямо противоположным выводам: часы на Земле, движущейся со скоростью υ относительно космического корабля, должны отставать от часов на корабле. Поэтому длительность полёта должна быть большей для космонавта, а не для жителей Земли.
Таким образом получается, что разность показаний часов на Земле и на космическом корабле после приземления последнего должна быть, с одной стороны, положительной, а с другой – отрицательной. Этот абсурдный результат разрешается в рамках общей теории относительности, которая не рассматривается в нашем курсе физики. Часы космонавта всегда должны идти медленнее, чем часы на Земле.
Интервал
Интервалом между событиями или расстоянием между двумя мировыми точками в четырёхмерном пространстве-времени называется величина
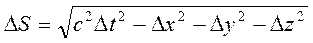 .
.
Пространство, в котором расстояние между двумя точками определяется таким выражением называется псевдоэвклидовым.
В обычном пространстве (эвклидовым)
 тогда
тогда  .
.
Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда 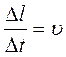 – скорость частицы и
– скорость частицы и
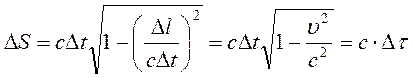 .
.
Поскольку с – константа, а Δ τ – инвариант, то и интервал Δ S также оказывается инвариантом.
В общем случае интервал может быть вещественным  , мнимым
, мнимым  и равным нулю (
и равным нулю ( , то есть, для светового сигнала).
, то есть, для светового сигнала).
Вследствие инвариантности интервала
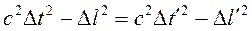 .
.
Пусть в К’-системе  (события пространственно совмещённые). Тогда для вещественного интервала
(события пространственно совмещённые). Тогда для вещественного интервала 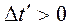 , т.е. события не могут быть одновременными. Поэтому вещественные интервалы называют времениподобными.
, т.е. события не могут быть одновременными. Поэтому вещественные интервалы называют времениподобными.
Мнимые интервалы называют пространственноподобными.