Для К’-системы, движущейся относительно К-системы с постоянной скоростью υ 0 вдоль оси ОХ получаем из преобразований Лоренца для координат и времени:
.
Так как
,
то
и 
и 
и 
Эти формулы выражают закон сложения (преобразования) скоростей в релятивистской кинематике.
В пределе при 
(при этом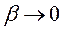 
) они приводят к классическому закону сложения скоростей в классической механике Ньютона:
; 
; 
и 
.
Как бы ни были близки к с скорости двух частиц, их относительная скорость друг относительно друга всегда меньше с.
Пример: две частицы движутся вдоль оси ОХ К-системы (лабораторной системы отсчёта) навстречу друг другу со скоростями υ 1 = 0,9 с и υ 2 =0,7 с.
Будем считать, что частица 2 неподвижна в К*-системе, т.е. 
. Тогда υ 1 = υх , а относительная скорость 
Получаем:
Элементы релятивистской динамики
Из принципа относительности следует, что математическая запись любого закона физики должна быть одинаковой во всех инерциальных системах отсчёта. Это означает, что уравнения, описывающие какое-либо явление в К’-системе, получаются из уравнений, описывающих то же самое явление в К-системе путём простой замены всех нештрихованных величин на штрихованные (условие ковариантности или условие лоренц-инвариантности).
Релятивистским импульсом материальной точки называют величину
.
Величину 
называют релятивистской массой, а т – массой частицы (иногда называют массой покоя), одинаковой во всех системах отсчёта (инвариантной).
Опыт подтверждает, что приведённый выше релятивистский импульс частицы действительно подчиняется закону сохранения независимо от выбора инерциальной системы отсчёта.
|
|
Основное уравнение динамики 
в релятивистской динамике принимает вид 
.
Видно, что сила F зависит от скорости 
.Т.е. вразных системах отсчёта её числовое значение и направление будут различны (неинвариантны).
Закон взаимосвязи массы и энергии
Найдём приращение кинетической энергии dK релятивистскойчастицы под действием силы 
на элементарном пути 
:
Рассмотрим теперь выражение . Введя левую и правую часть этого выражения в квадрат получаем:
Найдём дифференциал этого выражения, имея в виду, что т и с – постоянные величины:
.
Разделив на (2 т) и сравнивая с dK получаем
dK = c 2. dm p.
После интегрирования получаем:
Анализ выражения для кинетической энергии привёл Эйнштейна к важному выводу: тс 2 – это общая внутренняя энергия тела, из каких бы видов она ни состояла (электрическая, химическая и др.). Эту энергию назвали энергией покоя Е 0 = тс 2.
Величину Е = т р с 2 = Е 0 + К назвали полной энергией тела.
В полную энергию не включена потенциальная энергия тела во внешнем силовом поле, если таковое действует на тело.
Из закона взаимосвязи массы т и энергии покоя Е 0 тела видно, что масса тела, которая в нерелятивистской механике выступала как мера инертности (во втором законе Ньютона) или как мера гравитационного действия (в законе всемирного тяготения), теперь выступает в новой функции – как мера энергосодержания тела.