Тема: Системы счисления.

Задание 7.

1. Разобрать теоретический материал, примеры решение заданий.
2. Выполнить практические задания (задачи для тренировки)

Тема: Системы счисления.

Что нужно знать:

· перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной системами счисления

Полезно помнить, что в двоичной системе: · четные числа оканчиваются на 0, нечетные – на 1; · числа, которые делятся на 4, оканчиваются на 00, и т.д.; числа, которые делятся на 2k, оканчиваются на k нулей · если число N принадлежит интервалу 2k-1 £ N < 2k, в его двоичной записи будет всего k цифр, например, для числа 125: 26 = 64 £ 125 < 128 = 27, 125 = 11111012 (7 цифр) · числа вида 2k записываются в двоичной системе как единица и k нулей, например: 16 = 24 = 100002 · если известна двоичная запись числа N, то двоичную запись числа 2·N можно легко получить, приписав в конец ноль, например: 15 = 11112, 30 = 111102, 60 = 1111002, 120 = 11110002

· желательно выучить наизусть таблицу двоичного представления чисел 0-7 в виде триад (групп из 3-х битов):

X10, X8	X­2		X10, X8	X­2

и таблицу двоичного представления чисел 0-15 (в шестнадцатеричной системе – 0-F₁₆) в виде тетрад (групп из 4-х битов):

X10	X­2		X10	X­16	X­2
				A
				B
				C
				D
				E
				F

Пример задания:

Р-06. Сколько единиц в двоичной записи восьмеричного числа 1731₈?

Решение:

1) для решения достаточно знать двоичные коды чисел от 1 до 7, поскольку для перевода восьмеричного числа в двоичную систему можно достаточно каждую цифру отдельно записать в виде тройки двоичных (триады):

2) 1731₈ = 001 111 011 001₂

3) в этой записи 7 единиц

4) Ответ: 7

Ещё пример задания:

Р-04. Сколько единиц в двоичной записи десятичного числа 519?

Решение:

5) проще всего представить заданное число в виде суммы степеней числа 2:

519 = 512 + 7 = 2⁹ + 4 + 3 = 2⁹ + 2² + 2 + 1 = 2⁹ + 2² + 2¹ + 2⁰

6) количество единиц в двоичной записи числа равно количеству слагаемых в таком разложении

7) Ответ: 4

Ещё пример задания:

Р-03. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 63₁₀ * 4₁₀ 2) F8₁₆ + 1₁₀ 3) 333₈ 4) 11100111₂

Решение:

8) нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее из чисел, в которых ровно 6 единиц;

9) для первого варианта переведем оба сомножителя в двоичную систему:

63­₁₀ = 111111­₂ 4₁₀ = 100­₂

в первом числе ровно 6 единиц, умножение на второе добавляет в конец два нуля:

63­₁₀ * 4₁₀ = 111111­₂ * 100­₂ = 111111­00₂

то есть в этом числе 6 единиц

10) для второго варианта воспользуемся связью между шестнадцатеричной и двоичной системами счисления: каждую цифру шестнадцатеричного числа можно переводить отдельно в тетраду (4 двоичных цифры):

F­₁₆ = 1111­₂ 8₁₆ = 100­0₂ F8₁₆ = 1111 1000₂

после добавления единицы F8₁₆ + 1 = 1111 1001₂ также получаем число, содержащее ровно 6 единиц, но оно меньше, чем число в первом варианте ответа

11) для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду (группу из трёх) двоичных цифр:

333₈ = 011 011 011­₂ = 11011011₂

это число тоже содержит 6 единиц, но меньше, чем число в первом варианте ответа

12) последнее число 11100111₂ уже записано в двоичной системе, оно тоже содержит ровно 6 единиц, но меньше первого числа

13) таким образом, все 4 числа, указанные в вариантах ответов содержат ровно 6 единиц, но наибольшее из них – первое

14) Ответ: 1.

Ещё пример задания:

Р-02. Сколько единиц в двоичной записи числа 1025?

1) 1 2) 2 3) 10 4) 11

Решение (вариант 1, прямой перевод):

15) переводим число 1025 в двоичную систему: 1025 = 10000000001­₂

16) считаем единицы, их две

17) Ответ: 2

Возможные проблемы: легко запутаться при переводе больших чисел.

Решение (вариант 2, разложение на сумму степеней двойки):

1) тут очень полезно знать наизусть таблицу степеней двойки, где 1024 = 2¹⁰ и 1 = 2⁰

2) таким образом, 1025= 1024 + 1 = 2¹⁰ + 2⁰

3) вспоминая, как переводится число из двоичной системы в десятичную (значение каждой цифры умножается на 2 в степени, равной её разряду), понимаем, что в двоичной записи числа ровно столько единиц, сколько в приведенной сумме различных степеней двойки, то есть, 2

4) Ответ: 2

Возможные проблемы: нужно помнить таблицу степеней двойки.

Когда удобно использовать: · когда число чуть больше какой-то степени двойки

Ещё пример задания:

Р-01. Дано: 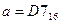и 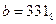. Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет неравенству a < c < b?

1) 11011001₂ 2) 11011100₂ 3) 11010111₂ 4) 11011000₂

Общий подход:

перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить.

Решение (вариант 1, через десятичную систему):

5)

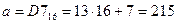
6)

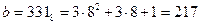
7) переводим в десятичную систему все ответы:

11011001₂ = 217, 11011100 ₂= 220, 11010111₂ = 215, 11011000₂=216

8) очевидно, что между числами 215 и 217 может быть только 216

9) таким образом, верный ответ – 4.

Возможные проблемы: арифметические ошибки при переводе из других систем в десятичную.

Решение (вариант 2, через двоичную систему):

1) 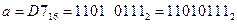(каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду);

2) 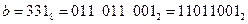(каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать);

3) теперь нужно сообразить, что между этими числами находится только двоичное число 11011000₂ – это ответ 4.

 

Возможные проблемы: запись двоичных чисел однородна, содержит много одинаковых символов – нулей и единиц, поэтому легко запутаться и сделать ошибку.

Решение (вариант 3, через восьмеричную систему):

1) 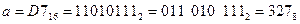(сначала перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной);

2) 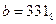, никуда переводить не нужно;

3) переводим в восьмеричную систему все ответы:

11011001₂ = 011 011 001₂ = 331₈ (разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, как в п. 1)

11011100 ₂= 334₈, 11010111₂ = 327₈, 11011000₂=330₈

4) в восьмеричной системе между числами 327₈ и 331₈ может быть только 330₈

5) таким образом, верный ответ – 4.

 

Возможные проблемы: нужно помнить двоичную запись чисел от 0 до 7 (или переводить эти числа в двоичную систему при решении).

Решение (вариант 4, через шестнадцатеричную систему):

1) 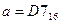никуда переводить не нужно;

2) 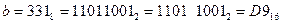(сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F);

3) переводим в шестнадцатеричную систему все ответы:

11011001₂ = 1101 1001₂ = D9₁₆ (разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F, как в п. 1)

11011100 ₂= DC₁₆, 11010111₂ = D7₁₆, 11011000₂=D8₁₆

4) в шестнадцатеричной системе между числами D7₁₆ и D9₁₆ может быть только D8₁₆

5) таким образом, верный ответ – 4.

Возможные проблемы: нужно помнить двоичную запись чисел от 0 до 15 (или переводить эти числа в двоичную систему при решении).

Выводы:

· есть несколько способов решения, «каждый выбирает для себя»;

· наиболее сложные вычисления – при переводе всех чисел в десятичную систему, можно легко ошибиться;

· сравнивать числа в двоичной системе сложно, также легко ошибиться;

· видимо, в этой задаче наиболее простой вариант – использовать восьмеричную систему, нужно просто запомнить двоичные записи чисел от 0 до 7 и аккуратно все сделать;

· в других задачах может быть так, что выгоднее переводить все в десятичную или шестнадцатеричную систему счисления.

Задачи для тренировки:

1) Сколько единиц в двоичной записи числа 195?

2) Как представлено число 263 в восьмеричной системе счисления?

1) 301₈ 2) 650₈ 3) 407₈ 4) 777₈

3) Как записывается число 567₈ в двоичной системе счисления?

1) 1011101₂ 2) 100110111₂ 3) 101110111₂ 4) 11110111₂

4) Как записывается число A87₁₆ в восьмеричной системе счисления?

1) 435₈ 2) 1577₈ 3) 5207₈ 4) 6400₈

5) Дано: 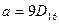, 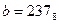. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

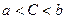1) 10011010₂ 2) 10011110₂ 3) 10011111₂ 4) 11011110₂