Генеральная совокупность и выборка. Статистическое распределение выборки.
Статестическая оценка. Свойства оценок (несмещённость, состоятельность, эффективность).
Интервальные оценки математического ожидания, дисперсии вероятности.
Статистическая оценка. Нулевая и альтернативная гипотеза. Ошибка первого и второго рода. Критические области. Критическая точка и ее определение по заданной вероятности.
Построение критерия для проверки гипотез. Проверка гипотезы о вероятности.
Проверкагипотезы о математическом ожидании нормально распределенной случайной величины при известной и неизвестной дисперсиях.
Проверка гипотезы о математических ожиданиях двух нормально распределено случайных величин при известной и неизвестной дисперсии.
Проверка гипотезы о законе распределения вероятностей генеральной совокупности (критерий Пирсона).
Корреляционная зависимость. Визуальное определения корреляционной зависимости по диаграмме рассеяния.
Оценка коэффициента корреляции по выборке, его экономическая интерпретация и свойства. Значимость выборочного коэффициента корреляции, коэффициент детерминации и его экономическая интерпретация.
Корреляционная матрица. Частный и множественный коэффициенты корреляции.
Математическая постановка задачи линейного программирования (ЗЛП). Формы записи ЗЛП: общая форма, каноническая форма.
Графический метод решения задачи линейного программирования.
24.Общая идея симплексного метода. Симплексная таблица, ее заполнения и преобразование. Критерий оптимальности опорного плана.
Формулировка двойственной задачи линейного программирования. Пары двойственных задач и их свойства.
26.Экономическая трактовка транспортной задачи (ТЗ) и ее математическая модель. Построение начального опорного плана транспортной задачи.
27.Нахождение оптимального плана транспортной задачи.
28.Постановка задачи динамического программирования. Принцип оптимальности и рекуррентные соотношения. Динамическое программирование (иначе, динамическое планирование) представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям. Для задач динамического программирования универсального метода решения не существует. Одним из основных методов динамического программирования является метод рекуррентных соотношений, который основывается на использовании принципа оптимальности. Принцип оптимальности – каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. На каждом шагу ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Процесс управления должен быть без обратной связи, т. е. управление на данном шаге не должно оказывать влияния на предшествующие шаги. Экономические задачи, решаемые методами динамического программирования:1)оптимальная стратегия замены оборудования;2)оптимальное распределение ресурсов;3)распределение инвестиций для эффективного использования потенциала предприятия;4)минимизация затрат на строительство и эксплуатацию предприятий;5) нахождение рациональных затрат при строительстве трубопроводов и транспортных артерий.
Математическая модель задач динамического программирования формулируется следующим образом.Пусть дана операция О, состоящая из m шагов (этапов). Эффективность операции характеризуется показателем «выигрышем» – W. Метод динамического программирования позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Процесс решения задачи разбивается на шаги. При этом нумерация шагов, как правило, осуществляется от конца к началу. Принцип погружения. Природа задачи, допускающей использование метода динамического программирования, не меняется при изменении количества шагов N, т. е. форма такой задачи инвариантна относительно N. В этом смысле всякий конкретный процесс с заданным числом шагов оказывается как бы погруженным в семейство подобных ему процессов и может рассматриваться с позиции более широкого класса задач. Основным принципом, на котором базируются оптимизация многошагового процесса, а также особенности вычислительного метода динамического программирования, является принцип оптимальности Р. Беллмана. Принцип оптимальности. Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующие решения должны быть оптимальными относительно состояния, полученного в результате первоначального решения. Реализация названных принципов дает гарантию того, что решение, принимаемое на очередном шаге, окажется наилучшим относительно всего процесса в целом, а не узких интересов данного этапа. Последовательность пошаговых решений приводит к решению исходной N-шаговой задачи. Принцип оптимальности имеет конструктивный характер и непосредственно указывает процедуру нахождения оптимального решения.
29.Постановка задачи нелинейного программирования. Метод множителей Лагранжа. Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции f(x1, х2,..., xn) на множестве D, определяемом системой ограничений 
где хотя бы одна из функций f или gi является нелинейной. По аналогии с линейным программированием ЗНП однозначно определяется парой (D, f) и кратко может быть записана в следующем виде 
Также очевидно, что вопрос о типе оптимизации не является принципиальным. Поэтому мы, для определенности, в дальнейшем по умолчанию будем рассматривать задачи максимизации. Как и в ЗЛП, вектор х* = (x1*,x2*,...,xn*) Î D называется допустимым планом, а если для любого x Î D выполняется неравенство f(x*) ≥ f(x), то х* называют оптимальным планом. В этом случае х* является точкой глобального максимума. С точки зрения экономической интерпретации f(x) может рассматриваться как доход, который получает фирма (предприятие) при плане выпуска х, а gi(х) ≤ 0 как технологические ограничения на возможности выпуска продукции. В данном случае они являются обобщением ресурсных ограничений в ЗЛП (аiх – bi ≤ 0). Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа. Многим читателям он должен быть известен из курса дифференциального исчисления. Идея данного метода состоит в сведении задачи поиска условного экстремума целевой функции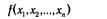 
на множестве допустимых значения D, описываемом системой уравнений 
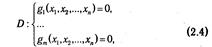к задаче безусловной оптимизации функции 
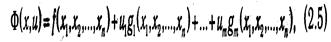где u Î Rm — вектор дополнительных переменных, называемых множителями Лагранжа. Функцию Ф(х,и), где x Î Rn, u Î Rn, называют функцией Лагранжа. В случае дифференцируемости функций f и gi справедлива теорема, определяющая необходимое условие существования точки условного экстремума в задаче (2.3)-(2.4). Поскольку она непосредственно относится к предмету математического анализа, приведем ее без доказательства.