Практическая работа №11.
Тема «Интегрирование по частям, интегрирование рациональных
Дробей и функций, содержащих квадратный трехчлен»
Найти первообразные заданных функций.
Вариант № 1,7,13,19,25,31. Вариант № 2,8,14,20,26.
1.  1.
1. 
2.  2.
2. 
3.  3.
3. 
Вариант № 3,9,15,21,27. Вариант № 4,10,16,22,28.
1. 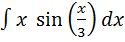 1.
1. 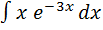
2.  2.
2. 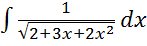
3.  3.
3. 
Вариант № 5,11,17,23,29. Вариант № 6,12,18,24,30.
1.  1.
1. 
2.  2.
2. 
3.  3.
3. 
Практическая работа №12.
Тема «Вычисление определенных интегралов и их
Геометрическое приложение»
Задание: п.1,2 – вычислить определенные интегралы;
п.3,4 – вычислить площади плоских фигур, ограниченных
заданными линиями.
Вариант № 1,8,15,22,29. Вариант № 2,9,16,23,30.
1.  1.
1. 

2.  2.
2. 
3. 2x – 3y + 6 = 0, y = 0, 3. x – y + 3 = 0, y = 0,
x = 3 x + y – 1 = 0
4. y =  , y = 1, x = 2 4. y =
, y = 1, x = 2 4. y = 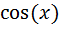 , y = 0,
, y = 0,
х =  и x =
и x = 
Вариант № 3,10,17,24,31. Вариант № 4,11,18,25.
1.  1.
1. 

2.  2.
2. 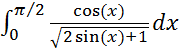
3. y =  , y = 0, x =0, 3. y = 3
, y = 0, x =0, 3. y = 3  , y = 0, x =
, y = 0, x = 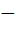 3,
3,
x = 3 x = 2
4. y =  , y = 0 4. y =
, y = 0 4. y = 
y = 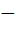 2x + 18
2x + 18
ПР №12
Вариант № 5,12,19,26. Вариант № 6,13,20,27.
1.  1.
1. 

2.  2.
2. 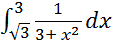
3. y =  , y = 0, x =
, y = 0, x = 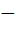 1, 3. x – 2y + 4 = 0, y = 0, x =
1, 3. x – 2y + 4 = 0, y = 0, x = 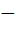 1,
1,
x = 2 x + 2y – 8 = 0, x = 6
4. y =  , y = 0 4. y =
, y = 0 4. y = 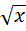 , y = 2, x = 9
, y = 2, x = 9
Вариант № 7,14,21,28.
1. 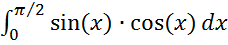
2. 
3. y = 0.5  + 2, y = 0, x = 1, x = 3
+ 2, y = 0, x = 1, x = 3
4. y =  , y = x + 2
, y = x + 2
Практическая работа №13.
Тема «Геометрические приложения определенного интеграла»
Вариант № 1.
1. Вычислить длину дуги плоской кривой, уравнение которой
y =  при
при 
 x
x 
 .
.
2. Найти объем тела, образованного при вращении вокруг оси ОХ кривой
y =  в промежутке от х = 0 до х =
в промежутке от х = 0 до х =  .
.
3. Найти площадь поверхности, образованной вращением одной полуволны
синусоиды y = 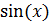 вокруг оси ОХ.
вокруг оси ОХ.
Вариант № 2.
1. Вычислить длину дуги плоской кривой, уравнение которой
y = 2  при 0
при 0  x
x  1.
1.
2. Найти объем тела, образованного вращением площади, ограниченной
полукубической параболой  , осью ОХ и прямой х = 2,
, осью ОХ и прямой х = 2,
вокруг оси ОХ.
3. Найти площадь поверхности, образованной вращением одной полуволны
косинусоиды y =  вокруг оси ОХ.
вокруг оси ОХ.
Вариант № 3.
1. Вычислить длину дуги плоской кривой, уравнение которой
y =  при 0
при 0  x
x  1.
1.
2. Найти объем тела, образованного вращением площади, ограниченной
линиями y =  , x = 0, y = 0, x = 1, вокруг оси ОХ.
, x = 0, y = 0, x = 1, вокруг оси ОХ.
3. Найти площадь поверхности, образованной вращением линии
y =  +
+  вокруг оси ОХ, в пределах от х = 0 до х = 2.
вокруг оси ОХ, в пределах от х = 0 до х = 2.
Практическая работа №14.
Тема «Приближенные методы вычисления определенных интегралов»
Задание: 1. Вычислить интеграл по формуле Ньютона-Лейбница.
2. Вычислить интеграл методом прямоугольников при n = 5.
3. Вычислить интеграл методом трапеций при n = 5.
4. Вычислить интеграл методом трапеций при n = 10.
Варианты заданий:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
ПР № 14
17.  18.
18. 
19.  20.
20. 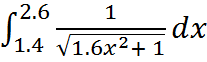
21.  22.
22. 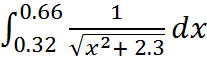
23.  24.
24. 
25.  26.
26. 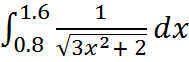
27.  28.
28. 
29.  30.
30. 
31. 
Практическая работа №15.
Тема «Решение задач на все действия с векторами»
Вариант № 1.
1. Найти скалярное произведение векторов 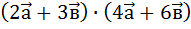 ,
,
где  = (3;4;5) и
= (3;4;5) и  = (1;2;6).
= (1;2;6).
2. Даны вершины треугольника А(3;2; 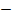 3), В(1;
3), В(1; 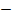 2;1), С(5;
2;1), С(5; 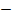 1;1). Найти угол А.
1;1). Найти угол А.
3. Найдите площадь параллелограмма, построенного на векторах
 = (1;1;
= (1;1; 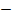 1) и
1) и  = (2;
= (2; 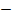 1;2).
1;2).
Вариант № 2.
1. Найти скалярное произведение векторов  ,
,
где  = (3;
= (3; 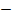 6;2) и
6;2) и  = (
= (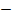 2;
2; 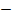 1;2).
1;2).
2. Даны вершины треугольника А 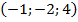 , В
, В  , С
, С  .
.
Найти угол В.
3. Найти синус угла между векторами  =
=  и
и  =
= 
Вариант № 3.
1. Найти скалярное произведение векторов  ,
,
где  =
=  и
и  =
=  .
.
2. Даны вершины треугольника А  , В
, В  , С
, С  .
.
Найти угол В.
3. Дан треугольник с вершинами А  , В
, В  , С
, С  .
.
Найти длину его высоты, проведенной из вершины С.
Практическая работа №16.
Тема «Составление уравнений прямой в пространстве и плоскости»
Вариант № 1.
1. Вычислить угол между прямой  =
=  =
= 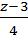 и плоскостью
и плоскостью
2x – 3y – 2z + 5 = 0.
2. Составить уравнение плоскости, перпендикулярной оси OZ и проходящей
через точку М  .
.
3. Найдите угол между плоскостями x – y + z + 1 = 0 и
2x + 3y – z – 3 = 0.
Вариант № 2.
1. Вычислить углы, образуемые прямой  =
=  =
=  с
с
координатными осями.
2. Составить уравнение плоскости, проходящей через точку М 
и параллельной плоскости x + 2y – 3z + 4 = 0.
3. Найдите расстояние между параллельными плоскостями
x 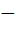 y + 2z – 4 = 0 и x
y + 2z – 4 = 0 и x 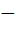 y + 2z + 10 = 0.
y + 2z + 10 = 0.
Вариант № 3.
1. Составить каноническое уравнение прямой и параметрическое уравнение
прямой, параллельной оси OZ и проходящей через точку М  .
.
2. Составить уравнение плоскости, параллельной оси OY и проходящей через
точки М  и К
и К  .
.
3. Найдите расстояние между параллельными плоскостями
x 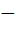 y +
y +  z – 5 = 0 и x
z – 5 = 0 и x  y +
y +  z + 3 = 0.
z + 3 = 0.