Деформационное упрочнение.
I. Упрочнение близкодействующими полями напряжений.
1. Гилман и Кульман-Вильсдорф считали, что близкодействующие поля напряжений вносят бóльший вклад в упрочнение материалов, чем дальнодействующие поля. Обосновывая свою теорию, они опирались на следующие факты:
а) на начальной стадии пластической деформации большое значение приобретает взаимодействие движущихся дислокаций с дефектами, оставленными предшествующей дислокацией. Для их продолжения необходимы более высокие напряжения. Например, после прохождения винтовой дислокации за ней остаются дефекты – дислокационные диполи: пара близкорасположенных дислокаций разного знака.
б) С увеличением плотности дислокаций уменьшаются расстояния между скоплениями дислокаций, являющимися точками закрепления дислокаций (образование скоплений объясняется с точки зрения дальнодействующих полей напряжений). Значит, уменьшается длина свободных участков способных выгибаться и образовывать новые петли. Как известно, критическое напряжение, при котором дислокационная петля захлопывается и начинает распространяться в кристалле, обеспечивая сдвиг, зависит от расстояния между точками закрепления – λ:
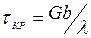
Чем меньше λ, тем выше напряжение течения.
в) Гилман и Вильсдорф считали, что основной причиной образования скоплений дислокаций является их ветвление, т.е. их способность искривляться и переплетаться друг с другом при взаимодействии с дефектами кристаллической решётки.
Теория Хирша и Мотта.
Хирш и Мотт считали, что основная причина упрочнения – это образование ступенек на дислокациях, снижающих их подвижность.
|
|
При пересечении дислокаций на них образуются ступеньки. Если ступенька соединяет 2 части одной дислокации, лежащие в разных плоскостях скольжения, она называется порогом. Если после пересечения дислокация остаётся в одной плоскости скольжения, то такую ступеньку называют перегибом. Различные варианты пересечения дислокаций изображены на рис 6.3-6.5.
|
| Рис. 6.3. Пересечение двух краевых дислокаций. Размер ступеньки: PP’ = b1, OO’ = b2. |
|
| Рис. 6.4. Пересечение краевой и винтовой дислокации |
|
| Рис. 6.5.Пересечение 2-х винтовых дислокаций |
При пересечении краевых дислокаций с параллельными векторами Бюргерса (Рис.6.3) на них образуются ступеньки с винтовой ориентацией, т.е. перегибы, которые могут скользить вдоль дислокации и аннигилировать. При пересечении краевой и винтовой дислокаций с перпендикулярными векторами Бюргерса образуется порог с краевой дислокацией на краевой дислокации и перегиб с краевой ориентацией на винтовой дислокации (Рис 6.4). Пересечение винтовых дислокаций изображено на рис 6.5. В этом случае образуются пороги с краевой ориентацией на обеих винтовых дислокациях.
С точки зрения развития пластической деформации последнее взаимодействие является наиболее важным, т.к. пороги с краевой ориентацией малоподвижны. Движение порога возможно вместе с дислокацией только неконсервативным путем (переползанием) с образованием вакансий или межузельных атомов. Такое движение требует дополнительной энергии, кроме того, скорость перемещения порога существенно ниже скорости основной части дислокации. Поэтому перемещение винтовых дислокаций с порогами краевой ориентации возможно только при более высоких напряжениях.
|
|
3. Барьерами для движения дислокаций являются «сидячие», т.е. неподвижные дислокации. Такими дислокациями являются частичные дислокации, у которых вектор Бюргерса направлен перпендикулярно плоскости скольжения (Рис.6.6). Например, такие дислокации присутствуют в ГЦК при образовании дефектов упаковки. Они могут перемещаться только переползанием.
«Сидячая» дислокация образуется при взаимодействии расщеплённых дислокаций, скользящих по пересекающимся плоскостям типа {111}. После взаимодействия образуется сидячая дислокация АВ, т.к. её вектор Бюргерса не лежит ни в одной из плоскостей скольжения. АВ отделена от частичных дислокаций DС и FE 2-мя участками дефекта упаковки. Такой комплекс из 3-х частей дислокации и 2-х дефектов упаковки называется барьером Ломер-Коттрелла.
|
| Рис. 6.6.Барьер Ломер-Коттрелла. |
II. Упрочнение дальнодействующими полями напряжений.
Теорию упрочнения дальнодействующими полями напряжений обосновал Тейлор, а в дальнейшем развили Зегер и Хирш.
Согласно данной теории, поле напряжений от дислокаций изменяется по закону:
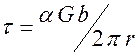, (6.1)
где α – коэффициент вида дислокаций (α = 1 – для винтовой дислокации, α = 3/2 – для краевой дислокации).
Это поле напряжений будет действовать на движущуюся дислокацию. Расстояние между дислокациями в среднем пропорционально их плотности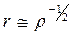 
, тогда внутренние напряжения:
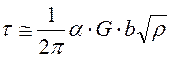(6.2)
Чтобы переместить дислокацию необходимо приложить внешние напряжения, превышающие по величине поля внутренних напряжений. При движении дислокаций более чем по одной системе плоскостей скольжения, им приходится пересекать дислокации, находящиеся в других системах скольжения, т.е. лес дислокаций.
|
|
При взаимодействии дислокации с лесом дислокаций большое влияние на напряжения сдвига оказывает дислокационная структура, т.е. степень неоднородности в распределении леса дислокаций, поэтому вводится параметр η, учитывающий неоднородность распределения.
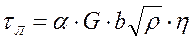(6.3)