СОЕДИНЕНИЕ ФАЗ ПРИЕМНИКА ТРЕУГОЛЬНИКОМ

На рис. 11.3, а изображена трёхфазная цепь, у которой источник и приёмник соединены треугольником. Режим работы фаз является незави­симым (кроме короткого замыкания в фазе, которое недопустимо), т. к. фазные напряжения приёмника определяются линейными нап­ряжениями источника и равны им, т. е. U_ф = U_л, а фазные токи при неравномерной нагрузке: I _ab = U _ab / Z _ab; I _bc = U _bc / Z _bc; I _ca = U_са / Z_ca.

Линейные токи определяют по формулам:

I _A = I _ab - I _ca; I _B = I _bc - I _ab; I _C = I _ca - I _bc,

причём I _A + I _B + I _C = 0.

Векторная диаграмма для случая неравномерной нагрузки (Z_ab = jX_ab, Z _bc = R_bc, Z _сa= R_ca - jX_ca) представлена на рис. 11.3, б.

В случае ра­в­но­мер­ной нагрузки (Z _ab = Z _bc = Z _ca = Z _ф) фазные токи при­ёмника I_ab = I_bc = I_ca = I_ф = . На векторной диаграмме как фаз­ные, так и линейные токи составля­ют сим­­­­­метричные звёзды (причём I_ab + I_bc+ + I_ca= 0 и I _A + I _B + I _C = 0), а соот­но­ше­ние между ними I_ф = I_л / (I_л = I_ф).

УЧЕБНЫЕ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ИХ ВЫПОЛНЕНИЮ

Задание 1. Экспериментально определить соотношения между линейными и фазными напряжениями и токами в различных режимах при соединении источника и приёмника по схеме звезда-звезда.

С этой целью:

1. Собрать схему (рис. 11.4, а) (или открыть файл LR11Y.ewb, находящийся в папке Models программы EWB) и устано­вить следующие режимы и параметры устройств и элементов:

- ЭДС трёхфазного источника G3F (рис. 11.4, б):

Е_A [220V/50Hz/0Deg]; Е_B [220V/50Hz/240Deg]; Е_С [220V/50Hz/120Deg];

- режим АС вольтметров V (R_v = 1 MW) и амперметров A (R_А = 1 mW);

- управляемые клавишами Q, W и S контакты;

- комплексы сопротивлений фаз приёмника (нагрузки, рис. 11.4, в):

Z _a = Z _b = Z _c = R + jX = [(20 + N) + j 30], Ом для четных N и

Z _a = Z _b = Z _c = R - jX = [(20 + N) - j 30], Ом для нечётных вариантов, где N - номер записи фамилии студента в учеб­ном журнале группы.

2. После проверки собранной схемы цепи запустить программу EWB.. Показания измерительных приборов для четырёхпроводной и трёхпроводной схем при равномерной и неравномерной нагрузке (состояние ключей и сопротивления фаз указаны в таблице) занести в табл. 11.1.

3. По данным эксперимента построить векторную диаграмму фазных напряжений и токов (в масштабе) потребителей четырёхпроводной цепи при неравномерной нагру­зке. Фазные углы определить по формуле . Срав­нить величину построенного вектора тока I _N с его экспериментальным значением.

Задание 2. Построить векторные диаграммы фазных напряжений и токов приёмника, соединённого звездой без нейтрального провода, при неравномерной нагрузке, при режимах ХХ и КЗ в фазе А, воспользовавшись калькулятором ElCalc (подпрограмма "Трёхфазные цепи") [щёлкните мышью на соответству­ющей пиктограмме меню].

Таблица 11.1

Вид цепи	Нагрузка	Измерено
Uл,B	Ua,B	Ub,B	Uc,B	UnN,B	Ia,А	Ib,А	Ic,А	IN,А
Четырехпроводная	Равномерная(ключи S и Q зам­к­нуты, W - разомкнут): Z ф = R ± jX
Неравномерная(ключи S и Q замкну­ты, W - разомкнут): Z a = R; Z b = ± jX; Z c = R ± jX
Трёх- про- водная	Равномерная(ключ Q замкнут, S и W - разомкнуты): Z ф = R ± jX									_
Неравномерная(ключ Q зам­кнут, S и W - разомкнуты): Z a = R; Z b = ± jX; Z c = R ± jX									_
Неравномерная (ключи S, Q и W разомкнуты): Z a =¥ (ХХ); Z b = ± jX; Z c = R ± jX									_
Неравномерная(ключ W зам­кнут, S и Q - разомкнуты): Z a = 0 (КЗ); Z b = ± jX; Z c = R ± jX									_

После ввода модуля линейного напряжения и сопротив­лений фаз (в комплексной форме) на экран калькулятора выводит­ся комплекс напряжения смеще­ния ней­тра­ли и ком­плексы фазных напряжений и токов. При моделировании режима ХХ принято Z_ф = R_ф ³ 20 МОм (нормированное сопротивление утечек при обрыве фазы), а режима КЗ - Z_ф = R_ф £ 0,1 Ом (нормиро­ванное сопротивление проводов при коротком замыкании фазы), причём ток I_{а (кз)} = 0 (при режиме КЗ фазы аn), а ток I_А в линейном проводе А протекает по перемычке, а не по сопротивлению фазы.

Сравнить значение напряжения U_nN с полученным в эксперименте значением, а также проверить равенство нулю суммы токов: I _a + I _b + I _c = 0.

Примечание. При построении векторной диаграммы измеренных напряжений приёмника, соединённого звездой без нейтрального провода, координаты точки n (конца вектора U _nN на комплексной плос­ко­­сти) находят методом засечек: из вершин равнобедренного тре­угол­ьника линейных напряжений (например, А и В) откладывают изме­рен­­ные величины U_а и U_b. Полученную точку n соединяют с вершиной С (получают вектор U _с). Положительные направления полученных фазных напряжений приёмника - от точки n к вершинам А, В и С треугольника. Далее, вычерчивают векторы фазных токов с учётом характера нагрузки фаз.

Задание 3. Экспериментально определить соотношения между линейными и фазными напряжениями и токами в различных режимах при соединении источника и приёмника по схеме звезда-треугольник.

С этой целью:

1. Собрать схему (рис. 11.5) (или открыть файл LR11D.ewb). Режимы и параметры устройств и элементов указаны в задании 1.

Таблица 11.2

Вид цепи	Нагрузка	Измерено
Uab,B	Ubc,B	Uca,B	IA, A	IB, A	IC, A	Iab, A	Ibc, А	Ica, А
	Трёхпроводная: звезда-треугольник	Равномерная(ключи Q и W зам­кнуты): Z ф = R ± jX
	Неравномерная (ключи Q и W замкну­ты): Z ab = R ± jX; Z bc = ± jX; Z ca = R
	Неравномерная (ключ Q разомкнут, W - замкнут): Z ab= R ± jX; Z bс= ± jX; Z ca=¥ (ХХ)
	Неравномерная (ключ Q pазом­кнут, W - замкнут): Z ab = R ± jX; Z bc = ± jX; Z ca = 0 (КЗ)

2. После проверки собранной схемы цепи запустить программу EWB. Показания измерительных приборов при равномерной и неравномерной нагрузке, в т. ч. при обрыве фазы ca и линейного провода C (состояния ключей и сопротивления фаз указаны в таблице) занести в табл. 11.2.

Убедиться в равенстве фазных, а также линейных токов при равно­ме­р­­ной нагрузке фаз приёмника.

3. По данным эксперимента построить векторные диаграммы фазных напряжений и фазных и линейных токов (в масштабе) цепи при неравномерной нагру­зке, в т. ч. при обрывах фазы са и линейного провода С. Фазные углы определить по формуле 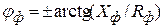. Обратить внимание на изменение линейных токов при обрыве фазы са и фазных токов при обрыве линейного провода С.

Срав­нить величи­ны построенных линейных векторов токов I_А, I_В и I_С с их экспериментальными значениями.