Откуда угловая (в рад/с) и циклическая (в Гц) резонансные частоты контура

Лабораторная работа 8 (LR8)

РЕЗОНАНСЫВ ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА

ЦЕЛЬ РАБОТЫ

Исследование явления резонанса в последовательном и параллельном колебательных контурах. Определение параметров колебательных кон­туров.

Изучение влияния добротности контура на характер нормированных частотных характеристик тока.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И РАСЧЁТНЫЕ ФОРМУЛЫ

ОБЩИЕ ПОЛОЖЕНИЯ

Под резонансом понимают такой режим работы электрической цепи, при котором ее входное сопротивление имеет чисто резистивный характер и, следовательно, сдвиг фаз между напряжением и током на её входе равен нулю (j = 0).

Цепи, в которых возникают резонансные явления, называют резонансными цепями или колебательными контурами. Простейший колебательный контур содержит один индуктивный L и один емкостный С эле­менты, соединенные между собой и источником синусоидального напряжения последовательно (последовательный колебательный контур) или параллельно (параллельный колебательный контур).

Различают две основные разновидности резонансных режимов: резонанс напряжений и резонанс токов.

РЕЗОНАНС НАПРЯЖЕНИЙ

Резонанс напряжений (РН) возникает в последовательном колебательном контуре (рис. 8.1). В схему замещения цепи включен также элемент R, учитывающий все виды активных потерь в контуре (в катушке, конденсаторе, во внутреннем сопротивлении источника питания, в соединительных проводах).

Условием наступления РН в схеме рис. 8.1 является равенство нулю реактивного сопротивления на входе цепи:

Х_РН = Х_L(РН) - Х_C(РН) = 0

или w _РНL = 1/( w _РН C),

откуда угловая (в рад/с) и циклическая (в Гц) резонансные частоты контура

и .

Характеристическое (волновое) сопротивление r (в Ом) последовательного колебательного контура равно его индуктивному или ёмкостному сопротивлению при резонансе:

Добротность Q контура – это отношение характеристического сопротивления r контура к резистивному R при резонансе:

.

Чем больше r и меньше R, тем добротнее контур, тем будут ýже частотные характеристики тока и напряжений на элементах контура. В радиотехнических контурах добротность Q = 100…1000; в электрических цепях добротность обычно не превышает 3…5.

Добротность показывает, во сколько раз напряжение на зажимах кон­денсатора U_C = U_L при резонансе большие напряжения питания контура U:

Ток I при РН имеет максимальное значение,

.

Зависимость нормированного тока N_i (f) = I (f)/ I_max и фазового угла j от частоты f напряжения на входе контура представлены на рис. 8.2.

Характерной особенностью режима РН является пре­вышение напряжений U_L и U_C входного напряжения U контура, первопричиной которого является ЭДС самоиндукции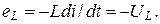

Векторные диаграммы напряжений на элементах контура до режима резонанса (а), при режиме резонанса (б) и после режима РН (в) представлен на рис. 8.3

Важнейшей характеристикой контура является его полоса пропускания (рис.8.2, а):

Df = f_в - f_н или Dw = w_в - w_н,

под которой понимают диапазон частот, в пределах которого значение нор­­мированного тока N_i (f) = I (f)/ I_max равно или больше 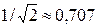. На гра­­ни­цах полосы пропускания, т. е. на частотах f_в и f_н (w_в и w_н), называемых вер­х­ней и нижней частотами среза, нормированный ток ак­тив­ная мощность P = 0,5 P_max, а угол j = ± 45°.

Приближённо полосу пропускания кон­тура определяют по формуле

или .

Заметим, что чем больше добротность, тем ýже полоса пропускания сигнала (рис. 8.4).

На практике параллельно конденсатору подключают приёмник, сопротивление ко­то­рого порядка R_н = 10…100 кОм.

При небольших значениях R_н полоса про­пускания D f увеличивается, а добротность контура снижается и равна

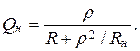
РЕЗОНАНС ТОКОВ

Резонанс токов (РТ) возникает в параллельном колебательном контуре (рис. 8.5), условием которого является равенство нулю входной реактивной проводимости

b_PT = b_{L ( PT )} – b_{C ( PT )} = 0 или

откуда резонансная угловая частота

,

где - резонансная частота контура без потерь (R ₁ = R ₂ = 0);

- характеристическое сопротивление контура.

Резонансные свойства цепи с двумя ветвями R ₁ L и R ₂ C (см. рис. 8.5) удобно изучать применительно к её эквивалентной схеме замещения с тре­мя параллельно соединёнными ветвями с параметрами g, b_L и b_C (рис. 8.6, а), равными

; ; .

Тогда добротность параллельного колебатель­ного контура

.

Практически добротность Q показывает кратность тока I_С в ветви с конденсатором (без резистора R ₂, см. рис. 8.5) при режиме РТ над током I_РТ на зажимах контура, т. е.

.

Ток I при РТ имеет минимальное значение, т. к. полная проводимость контура в этом режиме Y_РТ = Y_min, а сопротивление контура :

.

Амплитудно-частотная характеристика тока I (f) и фазо-частотная j (f) ха­рак­теристика реального и идеального контуров приведены на рис. 8.6, б и в.

Векторные диаграммы токов ветвей и тока на входе реального (а) и идеального (в) колебательных контуров для режима РТ представлены на рис. 8.6, б и г; ток I ₁ в первой ветви отстаёт от напряжения по фазе на угол j ₁, а ток I ₂ во второй ветви его опережает по фазе на угол j ₂ (рис. 8.6, б).

Ток I на входе контура, как правило, меньше токов I ₁ и I ₂ ветвей при режиме РТ, а для идеального контура ток I_РТ = 0 (рис. 8.7, г). При подключении приёмника R_н параллельно конденсатору (при 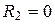, см. рис. 8.5) добротность нагруженного контура снижается тем сильнее, чем мень­ше R_н: , где .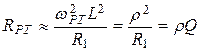

Полосу пропускания контура при небольшой расстройке определяют по формуле

или .