2.1. Определить отношение средних квадратичных скоростей молекул гелия и водорода при одинаковых температурах.
2.2. Средняя квадратичная скорость молекул газа равна 500 м/с при давлении 4·105 Па. Определить плотность газа.
2.3. Определить среднюю арифметическую и среднюю квадратичную скорости молекул газа, плотность которого при давлении 2·105 Пa равна 0,8 г/м3.
2.4. Во сколько раз средняя квадратичная скорость теплового движения пылинок, взвешенных в воздухе, меньше средней квадратичной скорости молекул кислорода, входящего в состав воздуха? Масса пылинки 10-8 г.
2.5. Два одинаковых сосуда содержат одинаковое число молекул кислорода. Сосуды соединены краном. В первом сосуде средняя квадратичная скорость молекул равна 400 м/с, во втором – 500 м/с. Какой будет эта скорость, если открыть кран, соединяющий сосуды?
2.6. При какой температуре средняя квадратичная скорость атомов гелия станет равной второй космической скорости на Земле?
2.7. При какой температуре молекулы кислорода имеют такую же среднюю квадратичную скорость, как и молекулы водорода при температуре 100 K?
2.8. Колба объемом 4 л содержит некоторый газ массой 0,6 г под давлением 200 кПа. Определить среднюю квадратичную скорость молекул газа.
2.9. Смесь гелия и аргона находится при температуре 1 200 К. Определить среднюю квадратичную скорость и среднюю кинетическую энергию атомов гелия и аргона.
2.10. Определить среднюю арифметическую скорость молекул газа, если их средняя квадратичная скорость равна 1 км/с.
2.11. Определить средние квадратичные скорости теплового движения молекул водорода, азота, кислорода при 0 °С.
2.12. Определить средний квадратичный импульс молекулы водорода Н2 при температуре 27 °С.
|
|
2.13. При какой температуре средняя квадратичная скорость молекул кислорода равна средней квадратичной скорости молекул азота при температуре 100 °С?
2.14. 
На рисунке схематично изображена молекула кислорода. Момент инерции молекулы кислорода относительно оси О равен 19,2·10-40 г·см3. Определить значение средней квадратичной частоты вращения молекулы кислорода при 27 °С относительно оси О.
2.15. Определить кинетическую энергию теплового движения всех молекул кислорода, занимающих объем 5,5 л при давлении 2·105 Па. Энергией, приходящейся на колебательные степени свободы, пренебречь.
2.16. Газ, состоящий из жестких двухатомных молекул, находится при температуре 300 К. Определить среднюю квадратичную угловую скорость вращательного движения молекулы, если ее момент инерции 2,1·10-39 г·см2.
2.17. Считать, что воздух состоит из молекул азота, кислорода, водорода и углекислого газа. Молекулы какого из газов обладают наибольшей средней скоростью?
2.18. Сравнить средние квадратичные скорости молекул двух газов с параметрами: a) p1=600 кПа, р=1,2 кг/м3; б) Р2=400 кПа, ρ2=0,8 кг/м3.
2.19. При какой температуре средняя кинетическая энергия теплового движения атомов гелия будет достаточна для того, чтобы атомы гелия преодолели земное тяготение и навсегда покинули земную атмосферу?
2.20. Частицы гуммигута диаметром 10-6 м участвуют в броуновском движении. Плотность гуммигута 1,2·103 кг/м3. Определить среднюю квадратичную скорость частиц при 17 °С.
2.21. В момент взрыва атомной бомбы температура достигает 107 °С. Считать, что при этой температуре молекулы полностью диссоциированы на атомы, а атомы ионизированы. Определить при этих условиях среднюю квадратичную скорость иона водорода.
|
|
2.22. Пользуясь функцией распределения Максвелла и определением относительной скорости u (относительная скорость равна отношению скорости молекулы υ к наиболее вероятной скорости υв), получить функцию распределения Максвелла в приведенном виде: 
.
2.23. Определить вероятность того, что какая-нибудь молекула кислорода при температуре 0 °С имеет скорость, точно равную наиболее вероятной скорости.
2.24. Перейти от функции распределения Максвелла по скоростям к функции распределения молекул газа по значениям энергии: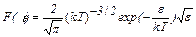 
, где ε – кинетическая энергия поступательного движения молекулы.
2.25. Доказать, что функция распределения Максвелла достигает максимального значения, если значение скорости молекулы равно значению наиболее вероятной скорости.
2.26. Сколько процентов молекул кислорода обладает скоростями, отличающимися от наиболее вероятной скорости не более чем на 1 %?
2.27. Сколько процентов молекул кислорода обладает скоростями, отличающимися от средней квадратичной скорости не более чем на 1 %?
2.28. Какая часть молекул азота при нормальных условиях имеет значения скоростей в интервале от 99 м/с до 101 м/с?
2.29. При какой температуре число молекул азота, обладающих скоростями в интервале от 299 м/с до 301 м/с, равно числу молекул азота, обладающих скоростями в интервале от 599 м/с до 601 м/с?
2.30. Сколько процентов молекул азота при температуре 280 К обладает скоростями в интервале от 500 м/с до 510 м/с?
2.31. Сколько процентов молекул кислорода обладает скоростями, отличающимися от наиболее вероятной не более чем на 10 м/с, при температуре 0 °С.
|
|
2.32. Водород находится при температуре 273 К. Определить отношение числа молекул водорода, обладающих скоростями в интервале от 2 000 м/с до 2 001 м/с, к числу молекул водорода, обладающих скоростями в интервале от 1000 м/с до 1001 м/с.
2.33. Определить температуру, при которой функция распределения молекул кислорода по скоростям имеет максимум при скорости 500 м/с.
2.34. Сколько процентов молекул кислорода обладает скоростями, отличающимися от наиболее вероятной скорости не более чем на 10 м/с при температуре 300 °С?
2.35. Определить температуру кислорода, при которой скоростям молекул 400 м/с и 600 м/с соответствуют одинаковые значения функции распределения Максвелла.
2.36. Определить высоту горы, если атмосферное давление на ее вершине равно половине атмосферного давления на уровне моря. Температуру считать одинаковой и равной 273 К.
2.37. Определить показания барометра на высоте Останкинской телевизионной башни, равной 540 м. Температуру считать одинаковой и равной 280 К. Атмосферное давление на поверхности Земли равно 760 мм рт. ст.
2.38. При подъеме аэростата барометр изменил свое показание на 11 кПа. На какой высоте находится аэростат, если на поверхности Земли барометр показывал 0,1 МПа? Температуру воздуха считать одинаковой и равной 290 К.
2.39. Чему равна концентрация молекул воздуха на высоте 2 км над уровнем моря? Давление на уровне моря 101 кПа, а температура 10 °С. Изменением температуры с высотой пренебречь.
2.40. Пылинки массой 10-10 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1 %. Температуру воздуха во всем объеме считать равной 27 °С.
2.41. У поверхности Земли концентрация молекул водорода почти в 106 раз меньше, чем концентрация молекул азота. На какой высоте концентрации молекул водорода и молекул азота будут равны? Температуру воздуха считать одинаковой и равной 0 °С.
2.42. При наблюдении в микроскоп взвешенных в жидкости частиц гуммигута обнаружено, что концентрация частиц в одной фокальной плоскости в два раза больше их концентрации в другой фокальной плоскости, расстояние между которыми 40 мкм. Температура жидкости 17 °С. Диаметр частиц 0,4 мкм, а плотность гуммигута на 0,2 г/см3 больше плотности окружающей жидкости. Определить по этим данным число Авогадро.
2.43. Определить массу водяного пара, заключенного в столбе атмосферного воздуха сечением 1,0 м2 и высотой 4,15 км. Температура воздуха во всех слоях постоянна и равна 15 °С. Парциальное давление паров воды на поверхности Земли 103 Па.
2.44. Толщина слоя воздуха, в пределах которого концентрация взвешенных в воздухе пылинок изменяется не более чем на 1%, равна 4,2 мм. Определить массу пылинки. Температуру воздуха считать одинаковой и равной 300 К.
2.45. На высоте 123 км от поверхности Земли концентрации молекул водорода и азота равны. Определить отношение концентраций молекул водорода и азота у поверхности Земли.
2.46. При наблюдении в микроскоп взвешенных в воде частиц гуммигута обнаружено, что концентрация частиц в одной фокальной плоскости в два раза больше их концентрации в другой фокальной плоскости, расстояние между которыми 40 мкм. Плотность гуммигута 1,2 г/см3. Температура воды 290 К. Определить диаметр частиц.