Формулы двойного аргумента

Занятие 5.

Повторим Формулы приведения

Выражения и т. д. можно записать проще: sin t, sin t, ctg t соответственно. Для этого используют формулы приведения. По сути, это не формулы, а определенный алгоритм преобразований.

При преобразовании тригонометрической функции 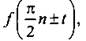где п ∈ Z, надо знать следующее.

1) Если n - четное число, то преобразуемая функция не меняется. Если n - нечетное число, то преобразуемая функция меняется на кофункцию (сопряженную функцию). Аргументом преобразованной функции будет t. Заметим, что кофункциями являются пары функций: синус и косинус; тангенс и котангенс.

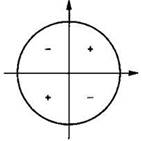
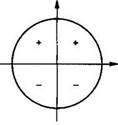2) Знак преобразованной функции совпадает со знаком исходной функции при условии, что угол t острый, т. е. t ∈ (0; π/2) (хотя реально он может быть любым). Знаки тригонометрических функций по координатным четвертям представлены на рисунке

 

Знаки синуса

 

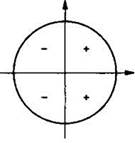
Знаки косинуса

 

Знаки тангенса и котангенса

 

Пример 1

Упростим выражение 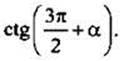Так как функция котангенса имеет аргумент 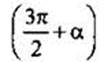и число n = 3 нечетное, то функция котангенса меняется на кофункцию - тангенс. В предположении, что угол α острый, получим, что угол 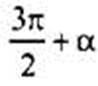лежит в IV четверти. В этой четверти знак котангенса отрицательный. В I четверти (угол α острый) все тригонометрические функции положительны (в том числе и тангенс). Поэтому перед тангенсом необходимо поставить знак «минус». В итоге имеем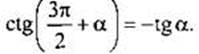

Пример 2

Упростим следующие выражения:

Пример 3

Приведем к тригонометрической функции угла из промежутка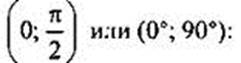

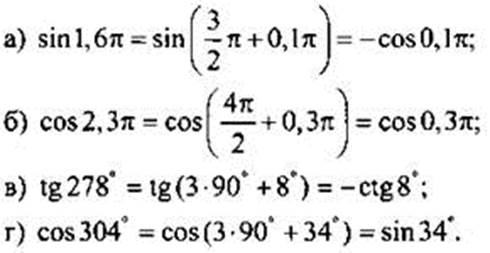
Пример 4

Упростим выражение:

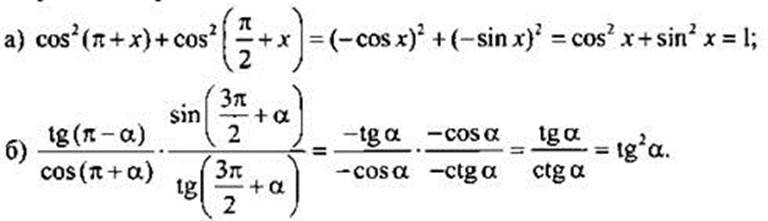
Синус, косинус и тангенс суммы и разности аргументов

Начнем с рассмотрения формул для синуса и косинуса суммы и разности аргументов (их также называют формулы сложения). Обратите особое внимание на эти формулы, так как из них достаточно просто могут быть получены практически все формулы тригонометрии.

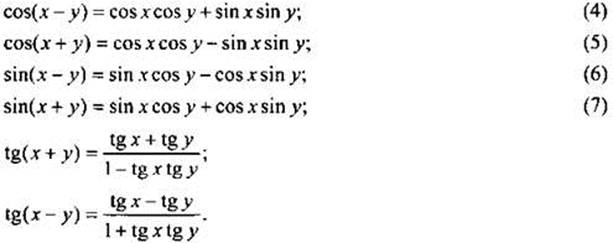
Пример 5

Вычислим cos 15°. Учтем, что 15 ͦ = 45 ͦ - 30 ͦ, и тогда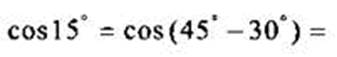

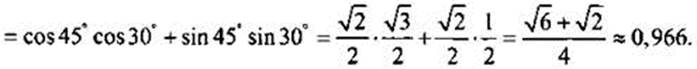
Таким образом, приведенные формулы позволяют расширить значения тригонометрических функций, представленных ранее в таблице.

Пример 6

Найдем 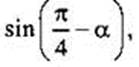если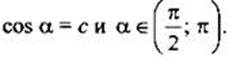

Используем формулу (6) и получим: 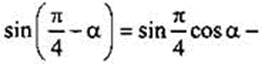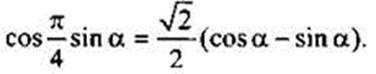Найдем sin α. Используя формулу основного тригонометрического тождества, получаем: 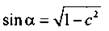(учтено, что 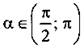и s sin α > 0). Тогда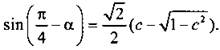

 

Формулы двойного аргумента

Формулы двойного аргумента (угла)

В формуле 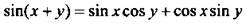положим х = у. Получим: 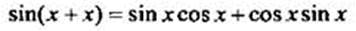или 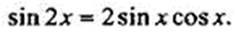Аналогично получается формула (9).

 

Связь тригонометрических функций с тангенсом половинного аргумента

В ряде случаев полезны следующие формулы:

Пример 7

Упростим выражения:

 

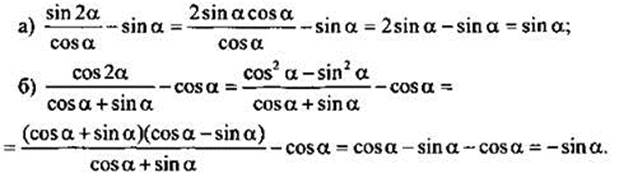
Пример 8

Пусть 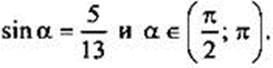Найдем sin2 α, cos2 α, tg2 α.

Сначала найдем cos α. Получим, применив основное тригонометрическое равенство: 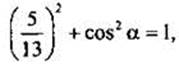откуда 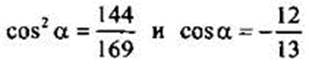(учтено, что 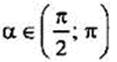и cos α < 0). Теперь найдем требуемые величины:

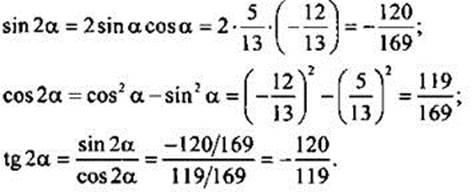
Из соотношений (8), (9) легко получить формулы понижения степени, которые очень часто используются при решении задач:

Из соотношений (8), (9) легко получить формулы понижения степени, которые очень часто используются при решении задач:

Пример 9

Докажем формулу (11). Преобразуем правую часть равенства: 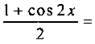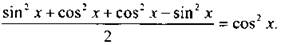Были учтены формулы (1) и (9). Аналогично доказывается и формула (10).

Используем формулы (8)-(9) для функций двойного аргумента:

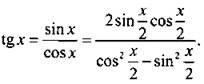Разделим числитель и знаменатель дроби на 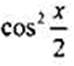и получим:

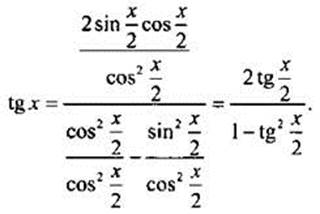
При этом возникают ограничения. Выражение 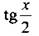имеет смысл (тогда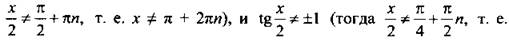

 

 

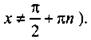
Занятие 6

Арксинус числа a (arcsinа) - такой угол α из промежутка 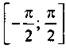, синус которого равен а, т. е.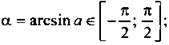

Арккосинус числаa (arccosа) - такой угол α из промежутка [0; π], косинус которого равен а, т.е.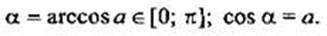

Арктангенс числа a (arctgа) - такой угол α из промежутка 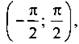тангенс которого равен а, т. е. 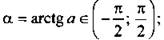tg α = а.

Арккотангенс числа a (arcctg а) - такой угол α из промежутка (0; π), котангенс которого равен а, т. е. 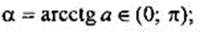ctgа = а.

Найдем:

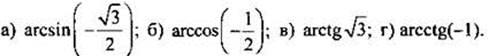
Учитывая определения обратных тригонометрических функций получим:

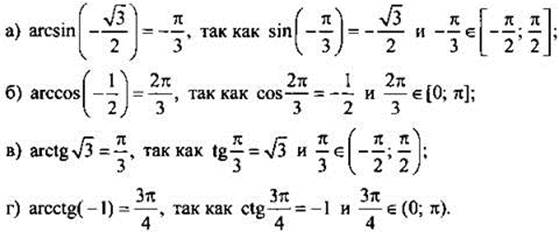
Пример Вычислим 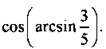Пусть угол α = arcsin 3/5, тогда по определению sin a = 3/5 и 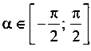. Следовательно, надо найти cos α. Используя основное тригонометрическое тождество, получим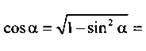 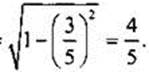Учтено, что 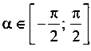и cos α ≥ 0. Итак,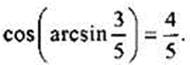

 

 

Занятия 7-8

1. Функция y = sin x, ее свойства и график

Обсудим построение графиков функций синуса и косинуса. Сначала построим график функции синуса на отрезке [0; 2π]. Отметим на оси ординат точки (0; -1) и (0; 1), на оси абсцисс - точку (2π; 0). Разделим отрезок [0; 2π] и единичную окружность на 8 равных частей (учтите, что длина отрезка [0; 2π] равна 2π ≈ 6,28). Каждая такая часть равна π/4. Для построения точки графика с абсциссой t используем определение синуса. Отметим точку Рt на единичной окружности и проведем через Рt прямую, параллельную оси абсцисс. Точка пересечения этой прямой и прямой х =tискомая, так как ее ордината совпадает с ординатой точки Рt и по определению sin t равен ординате точки Рt.

 

 

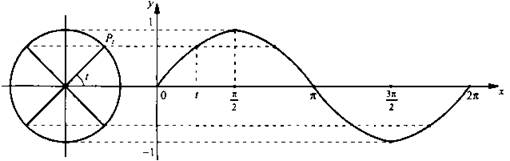
На рисунке приведено построение восьми точек графика. Соединяя их плавной кривой, получаем эскиз графика синуса на отрезке [0; 2π]. Для построения графика функции вне этого отрезка учтем периодичность функции синуса, т. е.sin(х + 2πn) =sinх (гдеn- произвольное целое число). Можно сказать, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси абсцисс (вправо и влево) на 2π, 4π, 6π и т. д. График функции синуса называется синусоидой. Отрезок [-1; 1] оси ординат, с помощью которого находили значения синуса, иногда называют линией синусов.

 

 

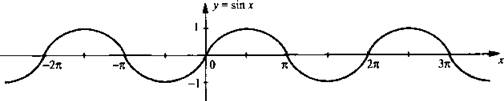
Используя построенный график, приведем основные свойства функции у =sinх:

1. Область определения D(y) = (-∞; +∞).

2. Функция нечетная (т. е. у(-x) = -у(x))> и ее график симметричен относительно начала координат.

3. Функция возрастает на отрезках вида 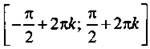и убывает на отрезках вида 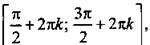где k∈Z.

4. Функция ограничена, т. е. -1 ≤ у(х) ≤ 1.

5. Наименьшее значение функции yнаим = -1 (достигается в точках вида 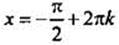) и наибольшее значение унаиб = 1 (достигается в точках вида ).

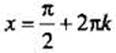6. Функция непрерывная.

7. Область значений Е(у) = [-1; 1].

8. Функция периодическая с наименьшим положительным периодом Т = 2π, т. е. у(х + 2 πk) = y(x).

Рассмотрим некоторые примеры.

Пример 1

Найдем наименьшее и наибольшее значения функции: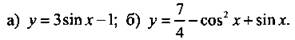

а) В силу ограниченности функции у =sinх имеем неравенство -1 ≤sinx≤1. Умножим все части этого неравенства на положительное число 3 и получим неравенство того же знака -3 ≤ 3sinx≤ 3. Вычтем их всех частей число 1: -4 ≤ 3sinх - 1 ≤ 2. Таким образом, yнаим = -4 и yнаиб = 2.

 

2. Функция у =cosx, ее свойства и график

Для построения графика функции косинуса учтем формулу приведения 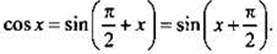Поэтому значение косинуса в любой точке x0 равно значению синуса в точке 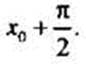Тогда график косинуса получается из графика синуса с помощью параллельного переноса на единиц влево вдоль оси абсцисс. Поэтому график функции у =cosх также является синусоидой.

 

 

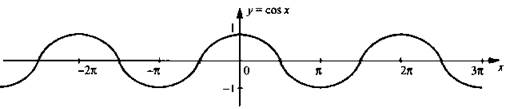
Перечислим основные свойства функции у =cosx:

1. Область определения D(y) = (-∞; +∞).

2. Функция четная (т. е. y(-х) =y(х)), и ее график симметричен относительно оси ординат.

3. Функция возрастает на отрезках вида [-π + 2πk; 2πk] и убывает на отрезках вида [2πk; π + 2πk], где k∈Z.

4. Функция ограничена, т. е. -1 ≤y(х) ≤ 1.

5. Наименьшее значение функции унаим = -1 (достигается в точках вида х = π + 2пk) и наибольшее значение унаиб = 1 (достигается в точках вида х = 2 πk).

6. Функция непрерывная.

7. Область значений Е(у) = [-1; 1].

8. Функция периодическая с наименьшим положительным периодом Т= 2π, т. е. у(х + 2 πk) = у(х).

Пример 2

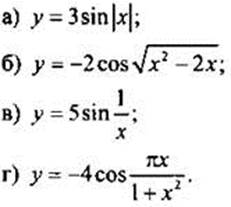Найдем область определения и область значений функции:

 

а) Для данной функции х может принимать любые значения, поэтому D(y) = R. Теперь найдем область значений функции. Так как -1 ≤sin|x| ≤ 1, то умножим все члены этого неравенства на 3 и получим - 3 ≤ 3sin|x| ≤ 3 или -3 ≤ у ≤ 3, т. е. Е(у) = [-3; 3].

б) Аргумент данной функции существует при условии, под корнем выражение ≥ 0. Решение этого неравенства х∈(-∞; 0]U[2; ∞), что и является областью определения функции у(х). Итак,D(y) = (-∞; 0]U[2; ∞). При изменении х в этих пределах величина 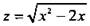меняется от 0 до ∞. Поэтому -1 ≤cosz≤ 1, тогда 2 ≥ -2cosz≥ -2, или или -2 ≤ у ≤ 2, т. е. Е(у) = [-2; 2].

в) Аргумент этой функции существует при условии х ≠ 0 и D(y) = (-∞; 0)U(0; ∞). При изменении х в таких пределах величина z= 1/x изменяется в промежутках (-∞; 0)U(0; ∞). Тогда 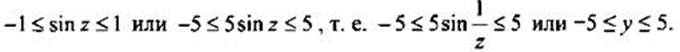Поэтому Е(у) = [-5; 5].

Пример 3

Установим четность или нечетность функции:

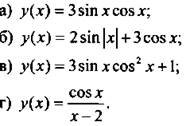
Для функций а-в область определения D(y) = R - симметричное множество. Для этих функций найдем у(-х).

а) 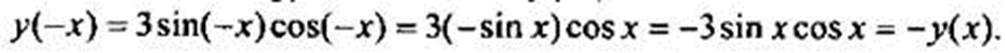Так как выполнено равенство y(-x) = -у(х), то данная функция по определению нечетная.

б) 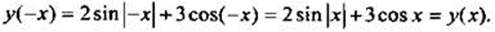Так как выполнено равенство y(-x) = у(х), то данная функция по определению четная.

в) 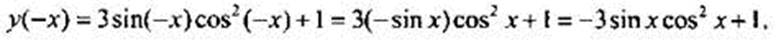Видно, что равенство y(-х) = -y(х) не выполняется, так как перед числом 1 один и тот же знак «плюс». Равенство у(-х) = у(х) также не выполняется, так как знаки перед первыми слагаемыми в этих функциях противоположны. Поэтому данная функция не является ни четной, ни нечетной, т. е. определенной четности не имеет.

г) Область определения данной функции D(у) = (-∞; 2)U(2; ∞) не является симметричной, так как точка х = -2 входит в эту область, а симметричная точка х = -(-2) = 2 не входит. Поэтому данная функция определенной четности не имеет.

3. Периодичность функций у =sinх, у =cosx

Перейдем к следующему свойству функции - периодичности. Многие реальные явления и процессы имеют повторяющийся (периодический) характер. Например, минутная стрелка занимает одинаковое положение на циферблате часов через каждый час. Такого типа процессы называют периодическими, как и их функции.

Функцияf(х) называется периодической с периодом Т (Т - некоторое действительное число, отличное от нуля), если:

1) для любого х из области определения функции значение аргумента х ± Т также принадлежит области определения функции;

2) выполняется равенство f(x+T) =f(x) =f(x-Т). Обычно под периодом функции понимают наименьший из всех положительных периодов (основной период функции).

 

 

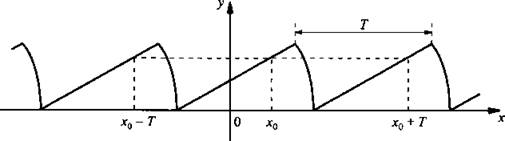
Исходя из определения тригонометрических функций, нетрудно установить, что период функцийsinxи cosх составляет 2π, период функций tgх и ctgх - π. Действительно, функции синуса и косинуса определены на всей числовой оси,sin(х + 2π) =sinх и cos(x+ 2π) =cosх для любого х. Аналогично области определения функций тангенса и котангенса включают как точку х, так и точки х ± π. При этом выполняются равенства tg(х + π) =tgх и ctg(х + π) =ctgx.

Найдем период функции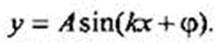

Предположим, что эта функция периодическая с основным периодом Т. Тогда должно выполняться равенство 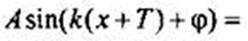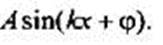Поэтому получим уравнение 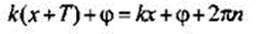или Т = 2πn, откуда 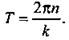Учитывая, что число Т – основной период данной функции, найдем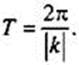

Аналогично можно показать, что для функции 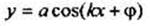основной период также 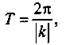для функци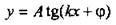й и 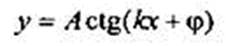основной период 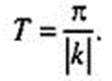Это обязательно надо помнить.

Отметим, что сумма, разность, произведение и частное двух периодических функций могут быть как периодической, так и непериодической функцией. В частности, алгебраическая сумма периодических функций будет функцией периодической, если периоды этих функций соизмеримы (т. е. если их отношение - число рациональное).

Тригонометрические функции - тангенс и котангенс.

1. Функция у = tgx

 

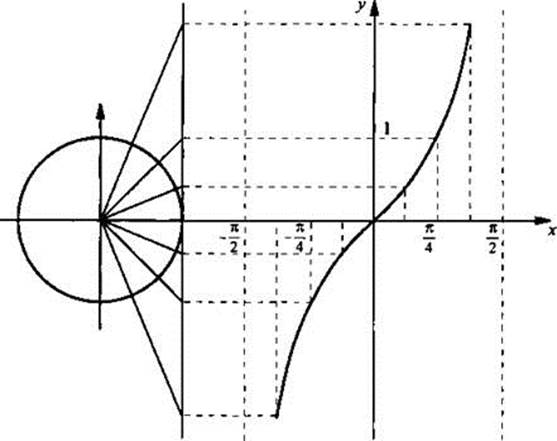
Остановимся на графиках функций тангенса и котангенса. Сначала обсудим построение графика функции у =tgх на промежутке 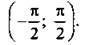Такое построение аналогично построению графика функции у =sinх, описанному ранее. При этом значение функции тангенса в точке находится с помощью линии тангенсов (см. рисунок).

 

 

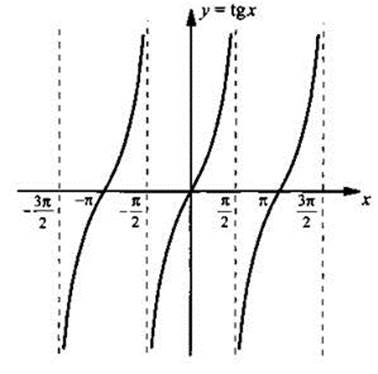Учитывая периодичность функции тангенса, получаем ее график на всей области определения параллельными переносами вдоль оси абсцисс (вправо и влево) уже построенного графика на π, 2π и т. д. График функции тангенса называют тангенсоидой.

Основные свойства функции у =tgх:

1. Область определения - множество всех действительных чисел, за исключением чисел вида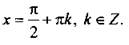

2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.

3. Функция возрастает на промежутках вида 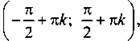где к∈Z.

4. Функция не ограничена.

5. Функция не имеет наименьшего и наибольшего значений.

6. Функция непрерывная.

7. Область значений Е(у) = (-∞; +∞).

8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + πk) = у(х).

9. График функции имеет вертикальные асимптоты