ПОСТРОЕНИЕ РАЗНОСТНЫХ СХЕМ ДЛЯ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1. Построение разностной схемы первого порядка. Введём сеточную функцию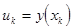 
, где k номер значения сеточной функции. Изменение аргумента определим следующим образом: 
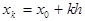, где 
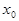=1.2 - значение аргумента на левом краю, k - номер дискретного значения изменения аргумента, h - величина шага. Таким образом исходное линейное дифференциальное уравнение:
y''+p(x)y'+q(x)y=f(x) (*)
примет вид:
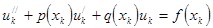(1)
Заменим выражения производных разностными соотношениями:
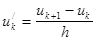(2)
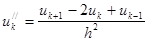(3)
подставив выражения (2) и (3) в (1) и сгруппировав сомножители при одинаковых номерах значений сеточной функции получим следующее выражение:
(4), где
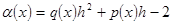
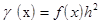
(4) определяет систему уравнений для нахождения значений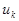 
. Эта система не может быть решена, так как при k=0..N, туда будут входить значения 
.
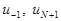Эти значения могут быть исключены из системы следующим образом.
В общем случае граничные условия заданы в виде:
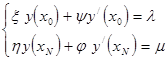(5)
x, y, l, h, j, m - некоторые числа, 
- значения функции и производных соответственно на левом и правом краях.
Здесь также заменим выражения производных разностными соотношениями:
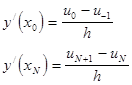
Подставив значения 
в (5) и выразив 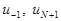, подставим в соотношение (4) записанное для k=0, k=N. После группировки и приведения к виду (4) получим систему уравнений, которую можно представить
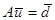(6)
А - матрица имеющая следующий вид:
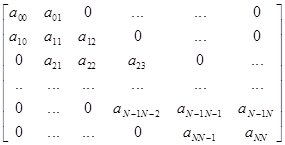
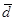- значения получающиеся в правой части (4).
Решая систему (6), найдём значения .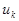
Точность данного метода R = ch, где c - некоторая постоянная величина.
2. Построение разностной схемы второго порядка. При построении такой численной схемы всё остаётся справедливо, что и для пункта 1., за исключением того, что аппроксимация первых производных в выражении (1) и граничных условиях (5) должна иметь порядок точности 
. Такую точность можно получить при приближении производной так (центральная разность):
В результате преобразований получаем выражение (4), но функции a(x), b(x), g(x) определяются следующим образом:
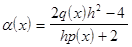
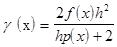
Заменяя выражения производных центральными разностями в краевых условиях и проделывая операции аналогичные описанным в пункте 1. Получим систему уравнений аналогичную (6). Матрица соответствующая системе уравнений будет иметь такую же структуру. Решая систему уравнений, находятся значения 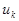. Точность данного метода 
, где т - некоторая постоянная величина.
МЕТОД СТРЕЛЬБЫРЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛНЫХ УРАВНЕНИЙ
Идея метода стрельбы заключается в следующем. Будем искать решение в виде:
,
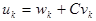где С некоторая константа. Подставляя в разностную схему второго порядка такое представление для функции 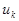и группируя слагаемые содержащие С, получим следующее выражение:
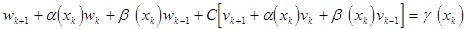(7)
a(x), b(x), g(x) - функции определённые для разностной схемы второго порядка.
Проделав то же самое и для краевых условий (5) получим:
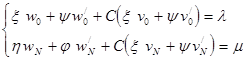(8)
Выражения (7) и (8) будут справедливо для любого С, при равенстве скобки при этом коэффициенте 0. Таким образом задача распадается на две: для 
и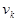 
.
Для 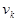задача будет такой:
(9)
Условие на левом краю выглядит так:
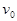выбирается произвольно(нельзя брать равной 0, так как получается тривиальное решение). Из (9) можно найти значения .
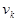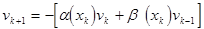(10)
Для определения необходимо знать 
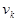. Её можно исключить, заменив производную в начальных условиях центральной разностью, выразить из полученного выражения, после подставить его в (10) записанное для k=0. Таким образом определим все значения , до N+1 включительно, но выражение для определения 
будет отличаться от (10).
Для задача будет такой:
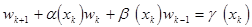(11)
Условие на левом краю выглядит так:
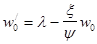
выбирается произвольно. Из (11) можно найти значения .
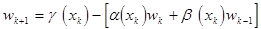(12)
Для определения необходимо знать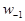 
. Действия по её исключению аналогичные исключению 
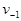. Таким образом определим все значения , до N+1 включительно, но выражение для определения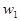 
будет отличаться от (12).
Воспользуемся для определения С вторым уравнением системы (8). Из него
Значения производных приближаются с помощью центральной разности.
Зная С, и 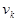, можно определить 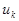по формуле, приведённой в начале раздела:
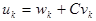
Точность метода в связи использования схемы разностной аппроксимации второго порядка .