Первая основная задача динамики

Динамика точки. Дифференциальные уравнения движения точки

Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

Уравнение второго закона динамики для материальной точки массой m запишется в виде

m⋅ a = ΣF_i (1)

где a - ускорение точки;

F_i - силы, действующие на точку, включая реакции связей.

Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений

m⋅ a_x = ΣF_xi

m⋅ a_y = ΣF_yi (2)

m⋅ a_z = ΣF_zi

где a_x, a_y, a_z - проекции ускорения точки на декартовы оси координат;

F_xi, F_yi, F_zi - проекция i-той силы на соответствующую ось.

Учитывая, что

получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки

или второго порядка относительно координат точки

Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений

где a_τ и a_n - касательное и нормальное ускорение точки;

F_τi, F_ni, F_bi - проекция i-той силы на касательную, нормаль и бинормаль соответственно.

Учитывая, что

a_τ = dV/dt, a_n = V²/ρ, a_b = 0

получим:

mdV/dt = ΣF_τi ,

mV²/ρ = ΣF_ni , (5)

0 = ΣF_bi .

В зависимости от того, что известно о движении точки, дифференциальные записывают или в декартовых или в естественных координатах.

нии уравнения второго порядка появляются две произвольных постоянных интегрирования.

Следовательно, при интегрировании системы (4) появятся шесть постоянных интегрирования. Таким образом, решение системы (4) будет иметь вид

x = x(t,C₁,C₂,C₃,C₄,C₅,C₆)

y = y(t,C₁,C₂,C₃,C₄,C₅,C₆)

z = z(t,C₁,C₂,C₃,C₄,C₅,C₆), (6)

где C₁,C₂,C₃,C₄,C₅,C₆ − постоянные интегрирования.

В зависимости от постоянных интегрирования получается целый класс решений, удовлетворяющих системе уравнений (4).

Чтобы получить конкретное решение, необходимо определить постоянные интегрирования.

Для этого необходимо знать значение координат и скорости точки в какой-либо момент времени (обычно в начальный), поэтому эти значения называют начальными условиями.

Таким образом, решение (6) можно переписать в виде

x = x(t,x₀,y₀,z₀,v_x0,v_y0,v_z0)

y = y(t,x₀,y₀,z₀,v_x0,v_y0,v_z0)

z = z(t,x₀,y₀,z₀,v_x0,v_y0,v_z0), (6’)

Первая основная задача динамики

 

В основе классической динамики лежат законы, впервые сформулированные и систематически изложенные И.Ньютоном в его «Математических началах натуральной философии».

 

В зависимости от того, что нам известно и что необходимо найти, в динамике рассматривают две основные задачи.

 

Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.

 

При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

где m – масса точки;

a – ускорение точки;

F_i – силы, действующие на точку.

В зависимости от способа задания движения точки, это уравнение можно записать по-разному.

Для векторного способа задания движения

где r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.

 

Для координатного способа задания движения точки

где x = x (t), y = y (t), z = z (t) – координаты точки, заданные как функции времени.

Для естественного способа задания движения точки

0 = Σ F_ib,

 

где dV/ dt – проекция ускорения точки на касательную в данной точке (касательное ускорение), V²/ ρ – проекция ускорения на нормаль (нормальное ускорение),

ρ – радиус кривизны траектории.

 

В правой части уравнений – проекции сил на касательную ΣF_iτ,

нормаль ΣF_in и бинормаль ΣF_ib.

 

По заданному закону движения точки определяются правые части этих уравнений, и далее может быть определена результирующая сила

 

– при координатном способе задания движения:

 

– при естественном способе или одна из составляющих сил:

 

Направление силы определяется с помощью направляющих косинусов:

 

cos (α) = R_x / R, cos (β) = R_y / R, cos (γ) = R_z / R (1.5)

где α, β, γ – углы между направлением силы и осями x, y, z соответственно.

 

Аналогично определяются углы, которые составляют силы с естественными осями координат.

Вторая основная задача динамики   Вторая, основная задача динамики точки заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.   Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.   Уравнение второго основного закона динамики для материальной точки массой m запишется в виде где a – ускорение точки; Fi – силы, действующие на точку, включая реакции связей.   Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений где ax, ay, az – проекции ускорения точки на декартовы оси координат; Fx, Fy, Fz – проекция i -й силы на соответствующую ось. Учитывая, что   получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки или второго порядка относительно координат точки.   Спроектировав уравнение (4.1) на естественные оси координат, получим следующую систему уравнений:   maτ = ΣFτi, man = ΣFni, 0 = ΣFbi. Учитывая, что 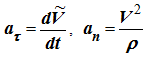где V – алгебраическое значение скорости, получим 0 =ΣFbi.   В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых, или в естественных координатах.   Каждое дифференциальное уравнение дает целый класс решений, отличающихся друг от друга на некоторую постоянную величину. Чтобы получить решение конкретной задачи, должны быть заданы так называемые начальные условия, которые позволяют определить постоянные интегрирования. >> Дифференциальные уравнения относительного движения материальной точки

Теоретическая механика Содержание краткой теории Примеры решения задач Обзорный курс Литература