1. Согласно геометрическому смыслу производной и условию задачи
.
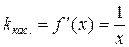Имеем: 
Интегральная функция y = ln ½x½ + C — это уравнение семейства кривых.
Т. A (1; 2) принадлежит кривой, следовательно, координаты точки должны удовлетворять уравнению кривой.
2 = ln 1 + C
2 = C
y = ln ½x½ + 2 — искомая интегральная кривая.
2. Согласно геометрическому смыслу производной и условию задачи
.
Имеем: 
.
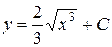— уравнение семейства кривых.
Точка 
принадлежит кривой, следовательно, координаты точки должны удовлетворять уравнению кривой.
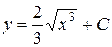
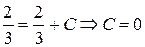
— искомая интегральная кривая.
3. Согласно геометрическому смыслу производной и условию задачи
.
Имеем: 
.
Интегральная функция y = —cos x + C — это уравнение семейства кривых.
Точка 
принадлежит кривой, следовательно, координаты точки должны удовлетворять уравнению кривой.
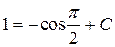
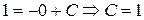
y = —cos x + 1 — искомая интегральная кривая.
4. Согласно геометрическому смыслу производной и условию задачи
.
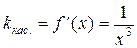Имеем: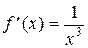 
.
Интегральная функция 
— это уравнение семейства кривых.
Точка 
принадлежит кривой, следовательно, координаты точки должны удовлетворять уравнению кривой.
— искомая интегральная кривая.
№2 Непосредственное интегрирование
2. Возведем числитель подынтегральной функции в квадрат и разделим его почленно на знаменатель. Затем, применяя основные свойства неопределенного интеграла 4, 5 и формулы 1 таблицы интегралов, получим:
Проверка
4. Применяя формулы 1, 4, 6 таблицы интегралов и основные свойства неопределенного интеграла 4 и 5, получим:
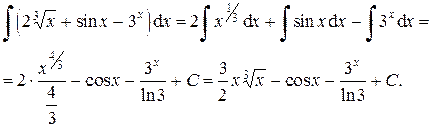
5. Представим подынтегральную функцию в виде степени с отрицательным показателем и применяя формулу 1 таблицы интегралов, получим:
.
Проверка
6. Разделим почленно числитель на знаменатель и, применяя основные свойства неопределенного интеграла 4 и 5 и формулы 1, 2 таблицы интегралов, получим:
Проверка
.
7. Воспользуемся формулой 
, основными свойствами 4, 5 и формулами 1,5 таблицы интегралов
8. Преобразуем знаменатель подынтегральной функции:
.
Добавляя в числитель x 2 и одновременно вычитая x 2, получим:
.
Разделим почленно числитель на знаменатель и, применяя основные свойства неопределенного интеграла 5, придем к двум табличным интегралам (формулы 1, 11 таблицы интегралов)
.
Окончательно имеем
.
9. Используя формулу 
, основные свойства неопределенного интеграла 4, 5 и формулы 1, 7 таблицы интегралов, получим:
.
10. Применяя основные свойства неопределенного интеграла 5 и формулы 9, 13 таблицы интегралов, получим:
.
11. Воспользуемся формулой косинуса двойного аргумента cos 2 x =
= cos2 x — sin2 x и представим числитель в виде произведения линейных множителей. Затем, применяя формулы 5, 6 таблицы интегралов, получим:
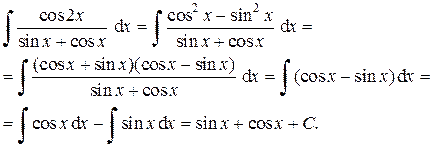
12. Преобразуем числитель и разделим его на знаменатель почленно. Затем, применяя основное свойство неопределенного интеграла 5 и формулу 3 таблицы интегралов, получим:
.
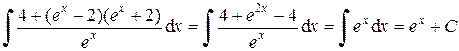№3 Вычисление неопределенных интегралов
методом подстановки
1. Вводим новую переменную
u = 5 x + 2,
тогда
Запишем исходный интеграл с новой переменной и новым дифференциалом
.
Возвращаясь к первоначальной переменной, получим
2. Выделим полный квадрат в знаменателе
x 2 + 4 x + 3 = (x 2 + 4 x + 4) — 1 = (x + 2)2 — 1
Вводим новую переменную u = x + 2.
Найдем d u:
d u = d (x + 2)
d u = d x.
Интеграл принимает вид
.
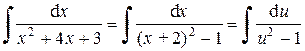Применяя формулу 12 таблицы интегралов, получим:
.
Возвращаясь к первоначальной переменной, получим:
.
3. Вводим новую переменную
u = 2 x + 7,
тогда
Запишем исходный интеграл с новой переменной и новым дифференциалом
.
Применяя формулу 2 таблицы интегралов, найдем
.
Возвращаясь к переменной x, получим:
.
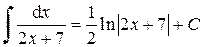4. Вводим новую переменную 
; тогда
u 2 = 1 + e x; e x = u 2 — 1; e xd x = 2 u d u, отсюда
Запишем исходный интеграл с новой переменной и новым дифференциалом:
.
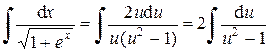Учитывая формулу 11 таблицы интегралов, имеем:
.
Возвращаясь к первоначальной переменной, получим:
.
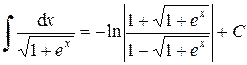7. Вводим новую переменную u = 4 x, тогда
Запишем исходный интеграл с новой переменной и новым дифференциалом:
.
Применяя формулу 7 таблицы интегралов, имеем:
.
Возвращаясь к первоначальной переменной, получим:
.
8. Вводим новую переменную 
, отсюда
u 3 = 4 — x; x = 4 — u 3; d x = —3 u 2d u.
Тогда
9. Вводим новую переменную
u = 3 x Þ 1—9 x 2 = 1 — u 2,
тогда
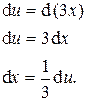
Запишем исходный интеграл с новой переменной и новым дифференциалом:
.
Применяя формулу 9 таблицы интегралов, получим:
.
Возвращаясь к первоначальной переменной, получим:
.
10. Вводим новую переменную 
.
Отсюда
u 2 = x 2 + 1; x 2 = u 2 — 1; 2 x d x = 2 u d u; x d x = u d u.
Тогда
.
11. Вводим новую переменную u = 4 x,
тогда 1 + 16 x 2 = 1 + u 2;
Запишем исходный интеграл с новой переменной и новым дифференциалом:
Применяя формулу 10 таблицы интегралов, получим:
.
Возвращаясь к первоначальной переменной, получим:
.
12. Вводим новую переменную
u = 3 + cos2 x,
отсюда d u = 2 cos x ž(—sin x) d x = —sin 2 x d x Þ
—d u = sin 2 x d x.
Тогда
№4 Вычисление неопределенных интегралов интегрированием по частям
1. Положим u = x и d v = sin x d x, тогда
Применим формулу интегрирования по частям, получим
2. Положим u = x и d v = cos x d x, тогда
.
Применяя формулу интегрирования по частям, получим:
.
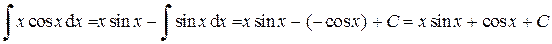3. Положим u = x + 1 и d v = e xd x, тогда
Применяя формулу интегрирования по частям, получим:
.
4. Положим u = ln x и d v = x 3d x, тогда
.
Применяя формулу интегрирования по частям, получим:
5. Положим u = ln x и d v = d x, тогда
Применяя формулу интегрирования по частям, получим:
.
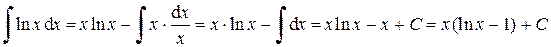7. Положим u = arctg x и d v = d x, тогда
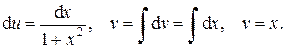
Применяя формулу интегрирования по частям, получим:
.
8. Положим u = x 2 и d v = e x d x, тогда
.
Применяя формулу интегрирования по частям, получим:
.
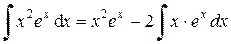Чтобы найти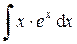 
, применим еще раз интегрирование по частям.
Положим u = x и d v = e x d x, тогда
и 
.
Окончательно имеем
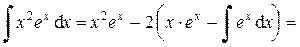
9. Положим u = arcsin x и d v = d x; тогда
Применяя формулу интегрирования по частям, получим:
10. Положим u = e x и d v = sin x d x, тогда
.
Применяя формулу интегрирования по частям, получим:
Возьмем по частям интеграл:
Тогда
Перенесем интеграл из правой части в левую и после приведения подобных членов, получим:
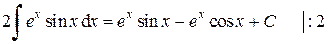
Окончательно имеем:
.
11. Положим u = x и 
, тогда
.
Применяя формулу интегрирования по частям, получим:
№5 Интегрирование рациональных функций
1. Так как x 3 - 5 x 2 + 6 x = x (x 2 - 5 x + 6) = x (x — 2)(x — 3), то подынтегральную функцию можно представить в виде суммы простейших дробей следующим образом:
,
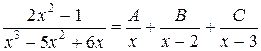где постоянные A, B, C найдем с помощью метода неопределенных коэффициентов.
Приведем правую часть последнего равенства к общему знаменателю
и, приравняв числители полученных дробей, определим неизвестные коэффициенты, исходя из тождества:
.
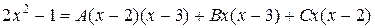Так как последнее равенство справедливо при любых значениях x, то выберем те значения x, каждое из которых обратило бы в нуль какой-либо из сомножителей правой части тождества.
Полагая x = 0, x = 2, x = 3 и подставляя поочередно эти значения в тождество, получим:
Из системы имеем: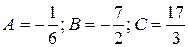 
.
Таким образом мы получаем следующее разложение рациональной дроби на простейшие
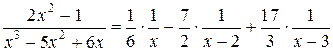
Интегрируя, находим:
.
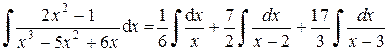По формуле 2 таблицы интегралов, получим:
.
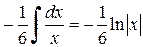Применяя метод подстановки и формулу 2 таблицы интегралов, найдем интегралы:
Окончательно имеем:
.
2. Знаменатель подыинтегральной дроби содержит однократные множители (x + 1) и (x + 2) и двухкратный множитель (x — 1)
Получим следующее разложение рациональной дроби на простейшие:
.
Неопределенные коэффициенты A, B, C и D найдем из тождества:
Видим, что при трех значениях x = -2, x = 1, x = -1 мы получаем обращение в нуль каких-либо слагаемых в последнем тождестве. Но нам надо найти 4 коэффициента, поэтому дадим x еще одно (любое) значение, например, x = 0. Подставляя поочередно эти четыре выбранные значения в тождество, получим:
Следовательно, разложение рациональной дроби на простейшие имеет вид:
а искомый интеграл равен:
.
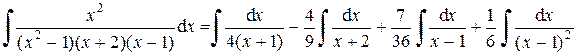Применяя метод подстановки и формулы 1, 2 таблицы интегралов, получим:
.
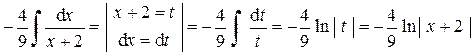
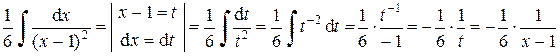Окончательно имеем:
.
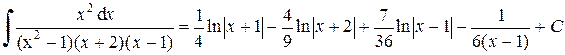3. Подынтегральная функция — правильная рациональная дробь. Преобразуем знаменатель этой дроби:
Тогда данную дробь можно разложить на простейшие следующим образом:
.
Неизвестные постоянные A, B, C найдем из тождества
.
Подставляя в тождество последовательно значения x = 1,
x = -3, x = -1, получим систему уравнений:
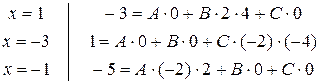
Из системы находим: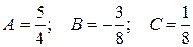 
.
Таким образом получим следующее разложение рациональной дроби на простейшие:
Интегрируя, находим:
.
Применяя метод подстановки и формулу 2 таблицы интегралов, получим:
.
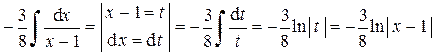
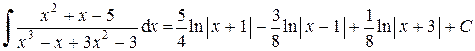Ответы к контрольной работе
Вариант 1
1. 
2. 
3. 
4. 
5. 
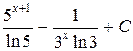
Вариант 2
1. 
2. Преобразуем
3. 
4. 
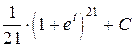
5. 
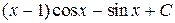
Литература
1. Власов В.Г. Конспект лекций по высшей математике, Москва, Айрис, 1996 г., стр. 113—121.
2. Тарасов Н.П. Курс высшей математики для техникумов, М., 1987 г., стр. 251—270.
3. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов, М., Наука, 1990 г., стр. 164—182.
4. Богомолов Н.В. Практические занятия по математике, М., «Высшая школа», 1997 г., стр. 188—204.
5. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах (II часть), Москва, «Высшая школа», 1967 г., стр. 5—23.
6. Гусак А.А. Пособие к решению задач по высшей математике, Минск, «Вышэйшая школа», 1968 г., стр. 350—378.
7. Шипачев В.С. Задачник по высшей математике, М., «Высшая школа», 1998 г., стр. 82-101.