АРИФМЕТИЧЕСКОЕ ЛИНЕЙНОЕ ПРОСТРАНСТВО

Рассмотрим множество Rn строк длины n.

Rn={(x_i,..,x_n)|: x_iєR, i=1,...n} с операциями сложения и умножения на число:

Если А=(а₁, а₂,..,а_n)єRⁿ;

B=(b₁, b₂,..,b_n)єRⁿ; єR;

то А+В=(a₁+b₁, a₂+b₂,..,a_n+b_n), A=( a₁, a₂,.., a_n).

Очевидно, что для А, ВєRⁿ; єR:
1)A+B=B+A;

2) (A+B)= A+ B;

3) (bA)=( b)A;

4)( + )A= A+ A;

Нулевая строка =(0,..,0) обладает свойствами:

+А=А; АєRⁿ; A+ =A.

ЛИНЕЙНАЯ ЗАВИСИМОСТЬ СТРОК

Пусть A₁,A₂,..,A_n є Rⁿ,

₁, ₂,.., _nє R.

₁A₁+ ₂A₂+...+ _nA_n

-это называется линейной комбинацией строк {A₁,..,A_n} с коэффициентами { ₁,.., _n}

(как само выражение, так и его результат).

Линейная комбинация называется тривиальной, если все =0 n;

Если хотя бы один их коэффициентов a не равен 0, то комбинация называется нетривиальной ( + +...+ =0).

Опр.:

Строки А₁,..,A_n є Rⁿ называются линейно зависимыми, если существуют их нетривиальные линейные комбинации, равные 0(нулевой строке).

₁,..λ_n: λ₁А₁,...,λ_nA_n = , причём ,..., = 0.

Строки А₁,...,А_n є Rⁿ называются линейно НЕзависимыми, если только тривиальная линейная комбинация строк равна 0, т.е. λ₁А₁+...+λ_nA_n = λ₁=...=λ_n = 0

Если строка В является линейной комбинацией строк А₁,...,А_n, то говорят, что В линейно выражается через А₁,...,А_n.

ТЕОРЕМА

Строки А₁,...,А_n линейно зависимы одна из них линейно выражается через остальные.

Доказательство:

1)Пусть А₁,...,A_n линейно зависима, значит ∃ λ₁,...,λ_n (не все = 0): λ₁А₁+...+λ_nA_n = .

Пусть λ₁=0, тогда А₁= - А₂ -...- А_n

2)Пусть А₁ линейно выражена через А₂,...,А_n. A₁= ₂A₂ +...+ _nA_n

Тогда А₁- ₂А₂-...- _nA_n = .

Получили нетривиальную линейную комбинацию, равную .

Пример:

Возьмём строки из Rⁿ:
E₁=(1,0,0,...,0)

E₂=(0,1,0,...,0) и т.д.

Е_n=(0,0,0,...,1)

Строки E₁,...,E_n линейно независимы.

Покажем это:

Пусть λ₁Е₁+λ₂Е₂+...+λ_nE_n = , но λ₁Е₁+...+λ_nE_n = (λ₁, λ₂,...,λ_n)

Если (λ₁, λ₂,..., λ_n) = 0, то λ₁=λ₂=...=λ_n= , т.е. линейная комбинация тривиальна.

Значит Е₁,...,Е_n линейно независимы.

Ч.Т.Д.

Замечание

Можно рассматривать столбцы как элементы Rⁿ.

 

Вопрос 10. Определение ранга матрицы. Теорема о базисном миноре.

1. Определение ранга матрицы.

Пусть A - матрица m×n. Обозначим ее строки A₁, A₂, … A_n, а столбцы - A⁽¹⁾, A⁽²⁾, … A⁽ⁿ⁾.

Выберем k строк и k столбцов и составим матрицу из элементов данных строк и столбцов. Определитель полученной матрицы называют минором порядка k (обозначают: , где i₁, i₂, …, i_k – номера строк, j₁, j₂,…, j_k – номера столбцов).

Определение: рангом (ненулевой) матрицы называют максимальный порядок ненулевых миноров.

Ранг нулевой матрицы равен нулю. Обозначения: r_A, rgA, rangA, rankA, rkA.

Если rkA = r, то в матрице существует ненулевой минор порядка r. Этот минор называется базисным. Строки и столбцы, образующие этот минор, называются базисными.

1. Теорема о базисном миноре.

Теорема:

1) Базисные строки и столбцы линейно независимы.

2) Все остальные строки и столбцы матрицы линейно выражаются через базисные строки (столбцы).

Доказательство:

1) Будем считать, что базисный минор находится в левом верхнем углу. Его порядок равен r.

Предположим, что строки A_1,…A_r линейно зависимы. Тогда одна из них линейно выражается через остальные. Пусть A₁ = λ₂A₂ + … +λ_rA_r.

Тогда:

.

Но это противоречит определению базисного минора.

2) Будем считать, что базисный минор находится в левом верхнем углу. Его порядок равен r.

Построим матрицу, добавив к базисному минору k-ю строку и j-й столбец.

Определитель этой матрицы равен нулю (Если j>r и k>r, то это минор порядка r+1, значит, он равен нулю).

Разложим определитель по j-му столбцу: Но – базисный минор, поэтому . Тогда . Получим . Т.е. . Теорема доказана (доказательство для столбцов - аналогично).

Следствия из теоремы:

1) Определитель матрицы равен нулю тогда и только тогда, когда одна из строк (столбцов) линейно выражается через другие.

Доказательство:

1. Если одна из строк линейно выражается через другие, то см. доказательство теоремы о базисном миноре.

2. Если определитель матрицы равен нулю, то базисный минор в матрице имеет меньший порядок, чем матрица. Следовательно, есть строка (столбец), не входящая(-ий) в базисный минор и линейно выражаемая(-ый) через строки (столбцы) базисного минора.

2) Ранг матрицы равен максимальному числу линейно независимых строк (столбцов).

Замечание 1: ранги исходной и транспонированной матрицы равны.

Замечание 2: дописывание или вычеркивание нулевой строки или нулевого столбца не меняет ранг матрицы.

 

Вопрос 11. Ранг произведения матриц.

Лемма: пусть , причем k>m. Если строки линейно выражаются через , то они линейно зависимы. Иначе: если большая система выражается через меньшую, то она линейно зависима.

Доказательство: пусть

Получим матрицу:

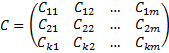. Т.к. k>m, то k>rkC. Следовательно, есть строка C_i, которая выражается через строки C_i1, C_i2,…,C_ir. (r=rkC). Значит, существует λ₁,…, λ_r такие, что C_i = λ₁C_i1+…+ λ_rC_ir.

C_ij=λ₁C_i1+…+ λ_rC_i1∀i=1…n. Но тогда:

B_i = C_i1A₁+…+C_imA_m = (λ₁C_i1,1+…+ λ_rC_ir,2)A₁+…+(λ₁C_i1,m+…+ λ_rC_ir,m)A_m = λ₁(C_i1,1A₁+…+C_i1,mA_m)+…+λ_r(C_ir,mA_m +…+C_ir,mA_m)= λ₁B_i1+…+λ_rB_ir, т.е. B₁…B_k – линейно зависимы.

Следствие: если B_1,…,B_k линейно выражаются через A₁,…,A_m (A_m∈ℝⁿ), причем B₁,…,B_k линейно независимы, то k≤m.

Замечание: , т.е. столбец C=AB является линейной комбинацией столбцов матрицы A.

Теорема о ранге произведения: пусть C=AB. Тогда rkC≤rkA и rkC≤rkB.

Доказательство: базисные столбцы матрицы C линейно выражаются через столбцы матрицы A. Следовательно, они линейно выражаются через базисные столбцы матрицы A. Следовательно (по следствию из леммы), количество базисных столбцов матрицы C не превосходит количества базисных столбцов матрицы A. Т.е. rkC≤rkA.

Т.к. базисные строки матрицы C линейно выражаются через строки матрицы B, то rkC≤rkB.

Следствие: умножение на невырожденную матрицу не меняет ее ранга.

Доказательство: т.к. C=AB, то rkC≤rkB. Т.к. A – невырожденная, то существует A^-1, тогда B=A^-1C. Поэтому rkB≤rkC. Значит, rkC=rkB.

 

Вопрос №12 Ранг матрицы и элементарные преобразования. Метод Гаусса нахождения ранга матрицы.

Теорема.

Элементарные преобразования не меняют ранг.

Доказательство.

Эквивалентные преобразования 1 типа эквивалентны умножению на матрицу Е₁=

Эквивалентные преобразования 2 типа эквивалентны умножению на матрицу E₂=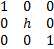

Эквивалентные преобразования 3 типа эквиваленты умножению на матрицу E₃=

Поскольку матрицы E₁,E₂,E₃ невырожденные то умножение на них не меняет ранга.

Метод Гаусса нахождения ранга матрицы.

Приводим матрицу к ступенчатому виду с помощью элементарных преобразований. Количество ступеней в этом ступенчатом виде равно рангу матрицы.

 

Неуверен в правильности написания матриц поэтому настоятельно советую сверить со своей записью.

Вопрос №13 Теорема Кронекера-Капелли

Пусть a₁₁x₁+…..+a_1nx_n=b₁

…………………………….

a_m1x₁+…..+a_mnx_x=b_m

система линейных уравнений. В матричном виде A*X=B. Присоединяем к матрице A столбец B.

A^*= Такая матрица называется расширенной матрицей системы линейных уравнений.

Теорема

Система совместна тогда и только тогда когда ранг исходной матрицы равен рангу расширенной матрице.

Доказательство.

1)Пусть система совместна тогда ₁,……. _n решение системы следовательно ₁A⁽¹⁾+ ₂A⁽²⁾+……+ _nA⁽ⁿ⁾=B следовательно B является линейной комбинацией столбцов матрицы A следовательно ранг расширенной матрицы равен рангу исходной.

2)Пусть ранг исходной матрицы равен рангу расширенной следовательно базисный минор исходной матрицы A является базовым для расширенной матрицы следовательно B линейно выражается через столбцы столбцы базисного минора матрицы A следовательно ₁,……. _n

₁A⁽¹⁾+ ₂A⁽²⁾+……+ _nA⁽ⁿ⁾=B следовательно ₁,……. _n решение системы.

 

14.Системы линейных уравнений и элементарные преобразования. Метод Гаусса решения систем линейных уравнений.

Утверждение 1 Преобразование, обратное элементарному – элементарное.

Утверждение 2 Пусть A*- расширенная матрица системы линейных уравнений A*X=B, тогда элементарные преобразования над строками A* не меняют множества решений системы.

Док-во. Пусть A** - матрица, полученная и А, с помощью элементарных преобразований. Если { ,…, } – решение исходной системы, то оно является решением получившийся системы. Значит, решений меньше не стало. Так как обратные элементарным – элементарные, то решений не могло стать больше. Итак, множество решений не изменилось.

Метод Гаусса. С помощью элементарных преобразований приведем расширенную матрицу к ступенчатому виду:

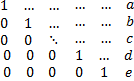
, где a,b,c,d,e – некоторые числа.

Не теряя общности, будем считать, что матрица имеет вид:

. Пусть r=rank A*

1) Если есть строка вида

, то система не совместна. (rkA ≠ rk A*)

2) Пусть таких строк нету, тогда м-ца соответствует системе

………………………………………………………….;

Обратный ход Вычтем из первой строки r-ю строчку с коэффициентом ; из второй строчки r-ю c коэффициентом и т.д. до (r-1) строчки. В r-ом столбце теперь стоят одни нули, кроме элемента .

То же самое делаем с (r-1) столбцом и т. Д. до первого столбца. Получим матрицу:

ó ;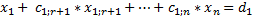

Или:

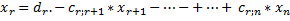
Назовем переменные .

Замечания:

1. Если r=n, то система имеет единственное решение.

2. Однородная система нетривиально совместна ór<n

Вопрос № 15.1)Подпространства в 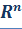.2)Структура множества решений однородной системы линейных уравнений. 3)Фундаментальная система решений.

1)Определение: Пусть . V называется линейным подпространством, если из того что x, y V → αx,βy для α,β.

Пример. X1,X2,…,Xn V= Множество всех линейных комбинаций строк X1,…Xn называется линейной оболочкой.

Определение: Упорядоченный набор строк E1,E2…En Vназывается базисом подпространства V, если 1) E1,E2…En линейно независимы. 2)Любая строка X V линейно выражается через E1,E2…En.

является подпространством любого пространства.

X=α1E1+…+αnEn – разложение X по базису E1,E2…En. Если V= , то говорят о базисе в .

Утверждение: Число строк в различных базисах одинаково. Доказательство: Пусть E1,E2,…,En и F1,F2,…,Fm – базисы подпространства V.Т.к. E1,E2…En базис, то F1,F2…Fm линейно выражается через E1,E2…En, а т.к. F1,F2…Fm линейно независима, то m≤n.Аналогично доказывается n≤m.

Число строк в базисе называют размерностью.(dimV=n).Если V= , то dimV=0.

2-3)

X1= +…+ .
….
Xr= …+ .

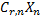Если (α1…αn) решения системы AX= , то (α1β1…αnβ1) тоже решение. Если (β1…βn) другое решение, то (α1+β1…αn+βn) тоже решение. Значит множество решений однородной системы AX= явл-ся подпространством в .

Пусть , Тогда получим столбец:

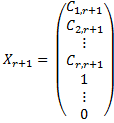
Аналогично проделав с ,то мы получим (n-r) решений и любое(все) решение системы линейно выражается через .При этом линейно независимы т.к. rk этой матрицы равен n-r.

Отсюда следует, что размерность подпространства решений линейной однородной системы равна n-r.

Определение. Система из n-r линейно независимых решений линейной однородной системы называется фундаментальной системой решений.

Фундаментальная система решений — базис в подпространстве решений линейной однородной системы.

Определение. Общим решением линейной системы называется выражение, позволяющее вычислить все (любое) решения системы.

Теорема. Если ранг r матрицы однородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде

Билет №16

Структура множества решений неоднородной системы линейных уравнений.

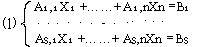ó AX=B(1’)

рассмотрим параллельно систему однородную

ó AX= (2’)

Утверждение 1:

Пусть X,Y – решения системы(1’)

Тогда (X-Y) – решение системы (2’)

Док-во:

A(X-Y)=AX-AY=B-B=

Теорема: Общее решение системы(1) может быть записано в виде

(3) XoH =XrH +C1E1 +…+ Cn-rEn-r = XrH + Xoo

Здесь: XrH – частное решение неоднородной системы. Xoo – общее решение однородной системы(2).

C1…Cn – произвольные вещественные числа.

Док-во:

Необходимо доказать:

1) " C1…Cn-r правая часть (3) является решением системы(1).

2) " решения системы(1) может быть записано в виде (3) при некоторых C1…Cn-r.

Докажем 1): подставим: XrH + C1E1 +…+Cn-rEn-r в (1):

A (XrH + C1E1 +…+ Cn-rEn-r) =

 

Докажем 2): пусть F – некоторое решение системы(1). В силу утверждения1 F- XrH является решением однородной системы(2) Þ$ C1…Cn-r: F- XrH = C1E1 +…+Cn-rEn-r

ÞF= XrH + C1E1 +…+Cn-rEn-r, где С1…Cn-r – некоторые действительные числа.

Вопрос 17. Комплексные числа. Алгебраические операции над комплексными числами. Комплексная плоскость.

Простейшее из квадратных уравнений 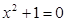не имеет корней среди действительных чисел. Попробуем расширить систему действительных чисел до такой системы чисел, чтобы это уравнение имело решение.

Возьмем всевозможные пары действительных чисел (a,b). Во множестве таких пар введем алгебраические операции:

1) Сложение: (a,b)+(c,d)=(a+c,b+d)

2) Умножение: (a,b)(c,d)=(ac-bd,ad+bc)

Заметим, что (a,o)+(b,0)=(a+b,0); (a,0)(b,0)=(ab,0). Пару (a,0) отождествляют с действительным числом a.

(0,1)(0,1)=(-1,0), т.е. (0,1)² = -1. Традиционно эту точку обозначают буквой i и называют мнимой единицей.

Т.к. (b,o)(0,1)=(0,b), то (0,b)=b i. Получаем, что (a,b)=(a,0)+(0,b)=a+b i. Будем записывать комплексные числа в виде z = a+b i, a,b ∈ R, i ²=-1.

Форма записи комплексного числа z = a+b i называется алгебраической. Число a называется действительной частью комплексного числа z (a =Re z), b - мнимой частью (b =Im z). Множество всех комплексных чисел обозначают .

 

Точка с координатами (a,b) соответствует комплексному числу z = a+b i. Число называют числом, сопряженным числу z = a+b i. На плоскости сопряжение – это симметрия относительно оси абсцисс.

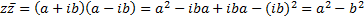
Пусть z₁=a₁+ib₁, z₂=a₂+ib₂, тогда:

1) z₁+z₂=(a₁+a₂)+i(b₁+b₂)

2) z₁-z₂=(a₁-a₂)+i(b₁-b₂)

3) z₁z₂=(a₁a₂-b₁b₂)+i(a₁b₂+a₂b₁)

4)

 

Вопрос 18. Тригонометрическая форма записи комплексного числа. Умножение и деление комплексных чисел в тригонометрический форме.

Модуль комплексного числа - это действительное число 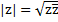. На плоскости | z |- это расстояние от начала координат до точки плоскости, соответствующей комплексному числу z.

Аргумент числа z – это угол в радианах, отсчитываемый от положительного направления Ox до радиус-вектора точки. Аргумент определен с точностью до

Если , то .

Получаем: – тригонометрическая запись комплексного числа.

Умножение, деление в тригонометрическом виде:

Пусть , тогда:

. При умножении модули сомножителей перемножаются, а аргументы складываются. Если , то , argz=argz₁+argz₂. Если , то argz=argz₁-argz₂

19. Возведение комплексного числа в n-ую степень. Формула Муавра. Извлечение корня n-ой степени из комплексного числа.

Формула Муавра: - (следует из умножения комплексных чисел в тригонометрическом виде)

Пример:

Найдём:

Пусть , тогда . Значит , (2 числа равны если модули совпадают, а аргументы отличаются на 2πk) т.е. .

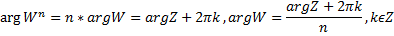
Итак, , ().

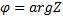При k=n: имеем n различных корней

Пример: найдём

K=0,1,2,3.

K=0: Z₁=

K=1: Z₂=

K=2: Z₃=

K=3: Z₄=

Любой комплексный многочлен имеет корень, тогда

N корней.

20.Линейные (векторные) пространства: определение, следствия из определения, примеры.

Определение: пусть V - некоторое множество с заданными операциями (сложение) и (умножение на число), для которого выполняются свойства:

1) (коммутативность сложения)

2) (ассоциативность сложения)

3) ()

4)

5)

6) (5 и 6 - дистрибутивность)

7)

8)

Тогда V называют линейным или векторным пространством над R.

Следствия:

1)Единственность

Пусть и - нейтральные элементы по сложению, тогда

2)Единственность противоположного элемента

Пусть и пусть ,

Тогда

3) ,

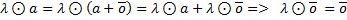
4) ,

5)Если , то выполняется хотя бы одно из равенств: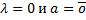

Примеры:

1)отрицательное линейное пространство

2)Геометрический вектор

3)Множество последовательностей

4)Множество сходящихся последовательностей

5)Множество бесконечно малых последовательностей

6)Множество функций на отрезке , - определяются естественным образом

7)Множество непрерывных функций

8)Множество матриц размера m*n

Билет №21

Линейная зависимость и независимость векторов. Базис и размер линейного пространства,примеры.

 

Определение: система векторов называется линейно зависимой,если существуют такие числа

(),(не все равные нулю одновременно),что =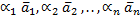

В противном случае система векторов является линейно независимой.

 

Пример:

 

 

(2,3)

 

(3,1)

 

 

Вектора , , образуют линейно зависимую систему.

= +

+

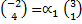Ранг матрицы показывает количество линейно независимых векторов в системе.

Размерность и базис линейного пространства

Пусть X — линейное пространство.

Определение. Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.

Будем обозначать n –мерное линейное пространство X_n, где n = dimX_n — размерность пространства X_n.

Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.

Замечания.

1. Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным.
2. Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называется бесконечномерным. Мы будем рассматривать, в основном, конечномерные линейные пространства. Бесконечномерные пространства являются предметом специального изучения.

Определение. Упорядоченная система векторов e ₁, e ₂, …, e _n О X называется базисом в X, если

• система векторов e ₁, e ₂, …, e _n линейно независима;
• любой вектор x пространства X может быть представлен в виде

x = 1 e 1 + 2 e 2 + … + nen.

(1)

• Выражение (1) называется разложением вектора x по базису e ₁, e ₂, …, e _n.
• Коэффициенты ξ₁, ξ₂, …, ξ _n в разложении векторапо данному базису определяются однозначно.

БИЛЕТ 22

Линейные операции над векторами

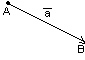Опр: Вектор - направленный отрезок. A – начало, В – конец. Если А=В =

1)Коллинеарные векторы – лежащие на одной прямой или на || прямых;

2) , , - компланарные, если будучи приведены к одному началу, лежат в одной плоскости;

3) = , если а)| |=| |; б)

Действия:

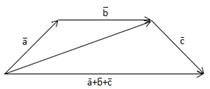
Сумма

 

Свойства сложения:

1) + = + 2) ( + )+ = +( + )

3)

Умножение вектора на число

Опр.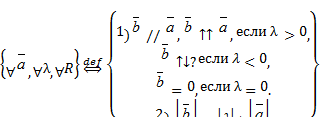

Свойства умножения:

1)

2) λ( + )=λ +λ

0

3) х()=х а)λμ˃0 (λμ) а//

б) λμ˂0 λ(μ )// λ(μа)↑↓ (λμ)

* = ((λμ) λ(μ )(μμ)

4) (λ+μ) =λ

Доказательство:

Пусть λ˃0, μ˃0

5) Теорема // , причем

Существует! λϵR; 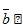=λ

Доказательство:

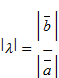
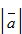˃0 λ=±

Если , то λ˃0 и λ= Действительно, если λ

Если λ=-- λ ↑↑

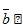
6)

<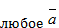