Интегральный признак Коши.
Рассмотрим ряд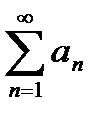 
, 
, 
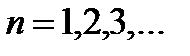
Если существует предел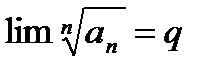 
То, 1) в случае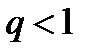 
ряд сходится;
2) в случае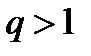 
ряд расходится.
В случае 
признак не работает, требуется дополнительное исследование.
Пример. Исследовать сходимость ряда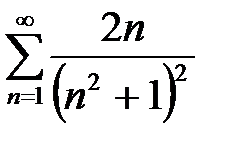 
Решение. Пусть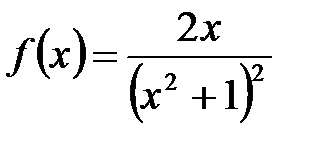 
.Применим интегральный признак. Так как
,
то есть несобственный интеграл 1-го рода сходится, тогда данный ряд сходится.
Теорема. Пусть члены ряда 
(1) положительны и не возрастают, т.е.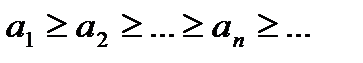 
и пусть 
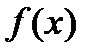- такая непрерывная, положительная и невозрастающая функция, что 
, 
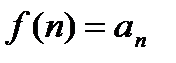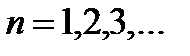
Тогда справедливы следующие утверждения:
1) если несобственный интеграл 
сходится, то и сходится и ряд (1).
2) если указанный интеграл расходится, то расходится и ряд (1).
Знакопеременные ряды. Абсолютная сходимость.
Рассмотрим ряд 
, ,
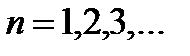
Если существует предел 
то,
1) в случае 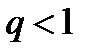ряд сходится;
2) в случае 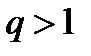ряд расходится.
В случае признак не работает, требуется дополнительное исследование.
Рассмотрим ряды, члены которых имеют чередующиеся знаки, т. е. 
(1), где 
.
Теорема (Лейбница). Если в знакочередующемся ряде (1) члены 
(2) - условие монотонного убывания и 
. То ряд (1) сходится, его сумма положительна и не превосходит первого члена.
Замечание.Теорема Лейбница справедлива, если условие монотонного убывания (2) выполняется, начиная с некоторого номера 
.
Пример.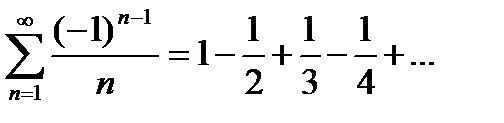 
сходится по теореме Лейбница, так как выполнено:
1) монотонное убывание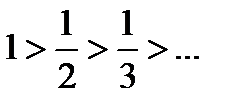 
2) 
Определение. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные (количество положительных и количество отрицательных членов бесконечно, т.к. если конечное плюс бесконечное, то можно отбросить конечное число членов).
Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Рассмотрим знакопеременный ряд 
(1)
и ряд, составленный из абсолютных величин
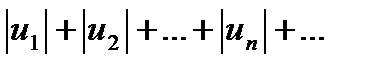(2).
Определение. Ряд (1) называется абсолютно сходящимся, если сходится ряд из абсолютных величин (2).
Теорема 1 (достаточный признак сходимости знакопеременного ряда). Если ряд (1) сходится абсолютно, то он сходится.
Пример.
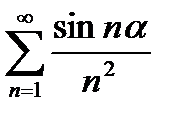, где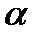 
- 
число. Рассмотрим ряд 
так как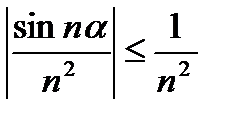 
, то по первой теореме сравнения ряд из абсолютных величин сходится, следовательно, исходный ряд сходится абсолютно.
Замечание. Теорема 1 является достаточным признаком сходимости знакопеременного ряда, но не необходимым:
Существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся.
Введем понятие условной сходимости знакопеременного ряда.
Определение. Ряд (1) называется условно сходящимся, если ряд из абсолютных величин 
расходится, а ряд 
сходится.
Примеры.
1) 
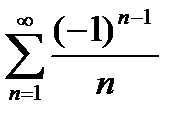, ряд из абсолютных величин 
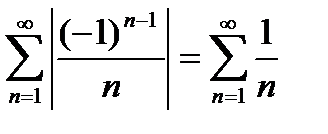расходится.
Но 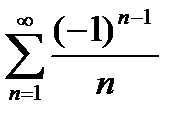сходится по теореме Лейбница. Следовательно, ряд сходится условно.
2) 
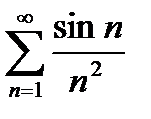, так как 
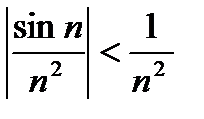и 
сходится, то по первой теореме сравнения ряд 
сходится.
Следовательно, исходный ряд сходится абсолютно.
Пример. Исследовать сходимость ряда.
.
Применим признак Лейбница. Так как
то
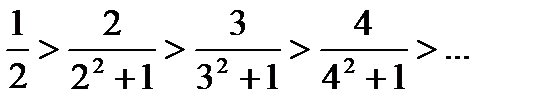
Следовательно, выполнено первое условие признака Лейбница. Далее, так как
то выполнено и второе условие. Значит, данный ряд сходится.
Знакочередующийся ряд. Признак Лейбница.
Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
1-1/2+1/3-1/4+1/2-1/6+…+ +((-1)n-1)/n +…-знакочередующийся ряд.
U1-U2+U3-U4+…+(-1)n-1Un+…=∑ (-1)n-1Un, (1)
где Un≥0.
Признак Лейбница: Если члены знакочередующегося ряда (1) удовлетворяют следующему условию:
1)U1>U2>U3>…>Un>… (убывающие);
2)limUn= 0 (общий член ряда =>0),
то ряд (1) сходится и S<U1.
Следствие: Если хотя бы один из вышеперечисленных условий нарушается, то ряд (1) расходится.
Доказательство:
А) n=2m (четное)
Sn=U1-U2+U3-U4+…+(-1)n-1Un;
S2m=(U1-U2)+(U3-U4)+…+(U2m-1-U2m);
Из условия 1 =>U1-U2>0, U3-U4>0, …, U2m-1-U2m>0.
S2,S4,S6,…,S2m-возрастающая последовательность.
S2m=U1-(U2-U3)-(U4-U5)-…-(U2m-2-U2m-1)-U2m>0.
S2m<U1 =>последовательность возрастает, ограничена сверху.
limS2m=S<U1 ряд сходится.
Б)n=2m (нечетное)
S2m+1=S2m+U2m+1
limS2m+1=lim(S2m+U2m+1)=limS2m+limU2m+1=limS2m=S<U1 рядсходящийся.