Задачи управления изначально ставятся, как правило, в терминах той области знаний, из которой они происходят (инженерия, физика, медицина, экономика и пр.). Для того чтобы иметь возможность исследовать подобные задачи математическими средствами, необходимо перевести их на математический язык, т.е. формализовать. Системы управления, которые рассматриваются в данной книге, относятся к классу динамических конечномерных непрерывных систем [4, 51].
Сформулируем ряд определений, касающихся этого класса систем.
Определение 1. Динамическая система  – понятие, состоящее из множеств
– понятие, состоящее из множеств  , переменных
, переменных  ,
, 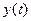 ,
,  и функции С, где
и функции С, где
 − область определения системы,
− область определения системы,
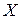 − пространство состояний системы,
− пространство состояний системы,
 − множество значений выходов системы,
− множество значений выходов системы,
 − пространство входов системы,
− пространство входов системы,
 – состояние системы,
– состояние системы,
 – выход системы,
– выход системы,
 – управление системой,
– управление системой,
С – непрерывная функция.
Здесь и далее: 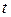 − независимая переменная, функция
− независимая переменная, функция  будет обозначаться символом
будет обозначаться символом 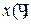 . Пусть
. Пусть  и
и 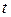 ‒ элементы из
‒ элементы из  , причем
, причем  . Символ
. Символ  будем использовать для обозначения сегмента (отрезка)
будем использовать для обозначения сегмента (отрезка) 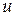 из
из  на множестве
на множестве  . Если
. Если 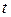 ‒ элемент
‒ элемент  ,
,  ‒ элемент
‒ элемент  и
и  – элемент
– элемент 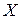 , то
, то  есть определенный элемент, который будем обозначать через
есть определенный элемент, который будем обозначать через  т.е.
т.е.
 , (В.1)
, (В.1)
называть выходом системы и  образуют пару «вход - выход» системы.
образуют пару «вход - выход» системы.
Пусть имеется непрерывная относительно своих аргументов функция  такая, что
такая, что
 . (В.2)
. (В.2)
Функцию 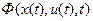 называют переходной функцией.
называют переходной функцией.
Уравнения (В.1) и (В.2) называют уравнениями выхода и состояния системы соответственно.
Определение 2. Динамическую систему  называют конечномерной, если
называют конечномерной, если
1. пространство состояний 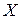 системы
системы  является евклидовым пространством
является евклидовым пространством  , т.е.
, т.е.  ;
;
2. множество значений выхода  есть евклидово пространство
есть евклидово пространство  ,
,  , т.е.
, т.е.  .
.
Отсюда следует, что непрерывная функция  преобразует
преобразует  в евклидово пространство
в евклидово пространство  . Число
. Число  , являющееся размерностью пространства
, являющееся размерностью пространства 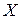 , называют порядком системы, а число
, называют порядком системы, а число  – размерностью выхода системы.
– размерностью выхода системы.
Определение 3. Говорят, что система  непрерывна (по времени), если множество
непрерывна (по времени), если множество  представляет собой открытый интервал
представляет собой открытый интервал  , который может быть равным всему
, который может быть равным всему  . Интервал
. Интервал  называют областью существования или интервалом определения системы.
называют областью существования или интервалом определения системы.
Определение 4. Динамическую систему  называют дифференциальной, если уравнения состояния и выхода системы имеют вид
называют дифференциальной, если уравнения состояния и выхода системы имеют вид
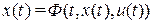 ,
,
где  есть решение системы дифференциальных уравнений
есть решение системы дифференциальных уравнений
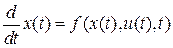 (В.3)
(В.3)
с начальными условиями  и
и
 .
.
Здесь 
Систему управления называют скалярной или SISO-сиcтемой (Single Input Single Output), если  . Если
. Если  или
или  , то такую систему называют векторной или MIMO (Multiple Input Multiple Output).
, то такую систему называют векторной или MIMO (Multiple Input Multiple Output).
Будем полагать, что функция  удовлетворяет условиям Липшица, т.е. существует постоянная
удовлетворяет условиям Липшица, т.е. существует постоянная  такая, что выполняются следующие неравенства:
такая, что выполняются следующие неравенства:

Здесь  и
и  ̶ производные функций
̶ производные функций  и
и  по
по  и
и  соответственно или
соответственно или  и
и  .
.
При этих условиях справедливы теоремы о локальном существовании, единственности и непрерывной зависимости на конечном интервале решения  уравнения (В.3) от начальных условий
уравнения (В.3) от начальных условий  и
и  .
.
Функция  называется непрерывной на интервале
называется непрерывной на интервале 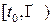 , если при любом положительном
, если при любом положительном  и любом
и любом 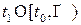 существует такое положительное число
существует такое положительное число  , что
, что  как только
как только  .
.
Различие непрерывной функции от равномерно непрерывной функции состоит в том, что положительное число  , которое можно подобрать для заданного
, которое можно подобрать для заданного  , в случае непрерывной функции зависит не только от
, в случае непрерывной функции зависит не только от  , но и от
, но и от  . Равномерная непрерывность предполагает, что по заданному
. Равномерная непрерывность предполагает, что по заданному  можно подобрать такое
можно подобрать такое 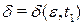 , что неравенство
, что неравенство  будет выполняться, как только
будет выполняться, как только  при любом
при любом 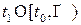 .
.
Лемма Барбалата. Если дифференцируемая функция  имеет конечный предел при
имеет конечный предел при  и ее производная
и ее производная  равномерно непрерывна, то
равномерно непрерывна, то  при
при  .
.
Доказательство. Докажем от противного. Допустим, что производная  не стремится к нулю при
не стремится к нулю при  . Но тогда существует положительное число
. Но тогда существует положительное число  такое, что для любого положительного числа
такое, что для любого положительного числа  , как бы велико оно ни было, существует
, как бы велико оно ни было, существует  , при котором справедливо неравенство
, при котором справедливо неравенство  . Следовательно, можно построить последовательность
. Следовательно, можно построить последовательность  , стремящуюся к бесконечности при
, стремящуюся к бесконечности при  и такую, что выполняется неравенство
и такую, что выполняется неравенство
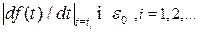
Так как производная  равномерно непрерывна, то существует такое положительное число
равномерно непрерывна, то существует такое положительное число  , что для любого
, что для любого 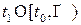 выполняется неравенство
выполняется неравенство
Так как производная  равномерно непрерывна, то существует такое положительное число
равномерно непрерывна, то существует такое положительное число  , что для любого
, что для любого 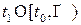 выполняется неравенство
выполняется неравенство
 ,
,
как только  . В частности, если принять
. В частности, если принять  , то из последнего неравенства получаем
, то из последнего неравенства получаем
 при
при  .
.
Из последних двух неравенств следует, что справедливо неравенство
 при
при 
Проинтегрировав обе части последнего неравенства на интервале  , получим
, получим
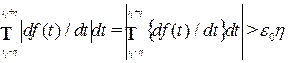 .
.
Равенство слева вытекает из того, что производная  на интервале интегрирования не меняет знака, так как на этом интервале она непрерывна и удовлетворяет ограничению
на интервале интегрирования не меняет знака, так как на этом интервале она непрерывна и удовлетворяет ограничению  .
.
Из последнего неравенства получаем неравенство
 ,
,
которое выполняется при любом  , как бы велико оно ни было. А это противоречит тому, что функция
, как бы велико оно ни было. А это противоречит тому, что функция  стремится к конечному пределу при
стремится к конечному пределу при  . Лемма доказана.
. Лемма доказана.
■
Следствие. Если дважды дифференцируемая на интервале 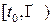 функция
функция  имеет конечный предел при
имеет конечный предел при  и вторая производная на этом интервале ограничена, то производная
и вторая производная на этом интервале ограничена, то производная  стремится к нулю при
стремится к нулю при  .
.
Определение 5. Две динамические системы  и
и  называют эквивалентными на интервале
называют эквивалентными на интервале  , если существует невырожденная матрица
, если существует невырожденная матрица  размерностью
размерностью  из постоянных элементов, такая, что
из постоянных элементов, такая, что

где  и
и  ̶ переменные состояний систем
̶ переменные состояний систем  и
и  соответственно.
соответственно.
Понятие эквивалентности означает, что если рассматривать динамическую систему  , описываемую уравнениями вида
, описываемую уравнениями вида
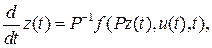
 ,
,
то траектории и выход системы будут теми же самыми, что и для системы  .
.
Отметим, что матрица  в общем случае может зависеть от
в общем случае может зависеть от  . Однако при каждом
. Однако при каждом  эта матрица должна быть обратима.
эта матрица должна быть обратима.
Пусть  ̶ группа преобразований. Напомним, что непустое множество
̶ группа преобразований. Напомним, что непустое множество  называют группой, если в
называют группой, если в  определена операция, ставящая в соответствие каждой паре элементов
определена операция, ставящая в соответствие каждой паре элементов  из
из  некоторый элемент
некоторый элемент  из
из  , так что выполнены следующие аксиомы:
, так что выполнены следующие аксиомы:
1. для всех трех элементов  верно равенство
верно равенство  ;
;
2. существует такой элемент  , что
, что  для любого
для любого  ;
;
3. всякий элемент  имеет обратный
имеет обратный  , для которого
, для которого  .
.
Пусть заданы две системы дифференциальных уравнений:
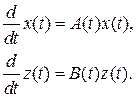
С группой  свяжем группу нестационарных преобразований
свяжем группу нестационарных преобразований

Нетрудно видеть, что отображение  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению
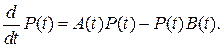
В теории управления важную роль играют некоторые структурные свойства систем. В частности, такие, как наблюдаемость, управляемость, устойчивость [21, 26, 32, 39, 81].
Пусть задана динамическая система (В.3)
 , (B.4)
, (B.4)
 .
.
Определение 6. Наблюдаемость. Говорят, что состояние 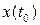 наблюдаемо, если для заданного управления
наблюдаемо, если для заданного управления  существует время
существует время  такое, что знания
такое, что знания  и выхода
и выхода 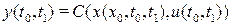 достаточно для определения
достаточно для определения 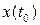 . Отметим, что время
. Отметим, что время  может зависеть от
может зависеть от  . Если каждое состояние
. Если каждое состояние 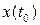 наблюдаемо в момент
наблюдаемо в момент  , то говорят, что система наблюдаема при
, то говорят, что система наблюдаема при  . Если же каждое состояние
. Если же каждое состояние  наблюдаемо в любой момент времени
наблюдаемо в любой момент времени  , то говорят, что система полностью наблюдаема.
, то говорят, что система полностью наблюдаема.
Определение 7. Управляемость. Если состояние  достижимо из
достижимо из  , т.е. существует такое
, т.е. существует такое  , где
, где  , которое переводит систему из состояния
, которое переводит систему из состояния  в
в 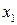 , то говорят, что состояние
, то говорят, что состояние 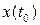 управляемо в момент
управляемо в момент  . Если каждое состояние
. Если каждое состояние 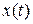 управляемо в момент
управляемо в момент  , то система полностью управляема.
, то система полностью управляема.
Определение 8. Достижимость. Состояние  называют достижимым или доступным из исходного состояния
называют достижимым или доступным из исходного состояния  в момент
в момент  по отношению к множеству
по отношению к множеству  , если существует элемент
, если существует элемент  такой, что
такой, что
 (В.5)
(В.5)
для конечного  .
.
Если через 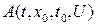 обозначить множество из
обозначить множество из 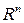 , которое состоит из всех значений
, которое состоит из всех значений  , достижимых из исходного состояния
, достижимых из исходного состояния  при
при  по отношению к множеству
по отношению к множеству  в момент
в момент  , то
, то  называют областью достижимости состояний в момент
называют областью достижимости состояний в момент  (из
(из  при
при  по отношению к
по отношению к  ).
).
Следует отметить, что, во-первых, из фактов наличия свойств управляемости, наблюдаемости и достижимости не вытекают какие-нибудь рекомендации по управлению состоянием или по наблюдению за состоянием системы. Во-вторых, наличие этих свойств является необходимым и достаточным для существования принципиальной возможности привести систему в любое состояние и наблюдать ее в любом состоянии. В-третьих, в общем случае наличие у системы свойств из определений
6, 7, 8, может оказаться, вообще никак не связано с решением задач управления и наблюдения. Другими словами, выполнение указанных свойств у конкретной системы определяет лишь ее «потенциальные возможности».
При рассмотрении различных практических задач управления существенную роль играет теория устойчивости. Сам термин «устойчивость» имеет много значений. Приведем определение понятия устойчивости по А.М. Ляпунову [46, 47].
Пусть непрерывная динамическая система описывается уравнением
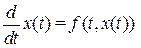 с начальным состоянием
с начальным состоянием  (В.6)
(В.6)
Обозначим через  шар радиуса
шар радиуса  с центром в начале координат в евклидовом пространстве
с центром в начале координат в евклидовом пространстве  с нормой
с нормой  (здесь
(здесь  – транспонированный вектор
– транспонированный вектор  ). Область определения (существования), как и ранее,
). Область определения (существования), как и ранее,  . Здесь
. Здесь  есть
есть  или заданное число,
или заданное число, 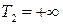 .
.
Будем считать, что функция 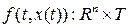 непрерывна и является липшицевой по аргументу
непрерывна и является липшицевой по аргументу  , т.е.
, т.е.

В теории устойчивости А.М. Ляпунова (1857 - 1918) исследуется на устойчивость одно решение. Пусть  - решение задачи (В.6), продолжимо до бесконечности, т.е.
- решение задачи (В.6), продолжимо до бесконечности, т.е.  существует на интервале
существует на интервале  причем
причем  при
при  .
.
Определение 9.1. Решение  задачи (В.6) называется устойчивым по Ляпунову, если для любого
задачи (В.6) называется устойчивым по Ляпунову, если для любого  существует
существует  такое, что все решения
такое, что все решения  задачи (В.6) бесконечно продолжимы вправо, как только
задачи (В.6) бесконечно продолжимы вправо, как только  , для таких решений справедливо неравенство
, для таких решений справедливо неравенство

т.е.  -трубка решений
-трубка решений  содержит все решения
содержит все решения  задачи (В.6), которые в начальный момент
задачи (В.6), которые в начальный момент  отстояли от
отстояли от  не более чем на
не более чем на 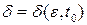 .
.
Решения (В.6)  и
и  называют невозмущенным (опорной траекторией) и возмущенным соответственно. Следует отметить, что рассматривается только одно устойчивое решение, а именно
называют невозмущенным (опорной траекторией) и возмущенным соответственно. Следует отметить, что рассматривается только одно устойчивое решение, а именно  , а не все решения уравнения (В.6).
, а не все решения уравнения (В.6).
Определение 9.2. Решение  называется равномерно устойчивым по
называется равномерно устойчивым по  , если для любого
, если для любого  найдется такое
найдется такое  , не зависящее от
, не зависящее от  , что
, что  , как только
, как только 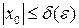 .
.
Определение 9.3. Тривиальное решение  уравнения (В.6) называется асимптотически устойчивым, если:
уравнения (В.6) называется асимптотически устойчивым, если:
1. оно устойчиво по Ляпунову;
2. для всякого  существует
существует  такое, что для
такое, что для 
 при
при  .
.
Множество  всех тех начальных условий
всех тех начальных условий  , для которых
, для которых  , называют областью притяжения тривиального решения в начальный момент
, называют областью притяжения тривиального решения в начальный момент  . Если
. Если  , то говорят, что решение
, то говорят, что решение  асимптотически устойчиво в целом (глобально асимптотически устойчиво).
асимптотически устойчиво в целом (глобально асимптотически устойчиво).
Если выполняется только условие 2 из определения 9.3, то говорят, что тривиальное решение является притягивающим (аттрактором). Из притяжения, вообще говоря, не следует устойчивость. Кроме случая скалярного обыкновенного дифференциального уравнения. Поэтому примеры, когда имеется притяжение, но нет устойчивости, можно построить только при  или для уравнений более общих, чем обыкновенные дифференциальные.
или для уравнений более общих, чем обыкновенные дифференциальные.
Определение 9.4. Тривиальное решение  системы (В.6) называется равномерно асимптотически устойчивым, если оно равномерно устойчиво и для любого числа
системы (В.6) называется равномерно асимптотически устойчивым, если оно равномерно устойчиво и для любого числа  найдутся числа
найдутся числа 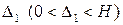 и
и  такие, что
такие, что  при
при  , а
, а 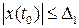 .
.
В общем случае требования равномерной асимптотической устойчивости сильнее требований асимптотической устойчивости.
Определение 9.5. Тривиальное решение  системы (В.6) называется экспоненциально устойчивым, если всякое решение
системы (В.6) называется экспоненциально устойчивым, если всякое решение  этого уравнения удовлетворяет оценке
этого уравнения удовлетворяет оценке
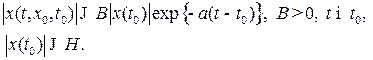
Отметим, что для линейных дифференциальных уравнений экспоненциальная устойчивость эквивалентна равномерной асимптотической устойчивости.
Рассмотрим, наряду с системой (В.6), систему с возмущением 
 (В.7)
(В.7)
Определение 9.6. Тривиальное решение  системы (В.7) называется устойчивым при постоянно действующих возмущениях, если для любого
системы (В.7) называется устойчивым при постоянно действующих возмущениях, если для любого  и
и  существует
существует  такое
такое  , что при
, что при  и
и  все решения системы (В.7) удовлетворяют условию
все решения системы (В.7) удовлетворяют условию  .
.
Определение 9.7. Тривиальное решение  системы
системы
 , (В.8)
, (В.8)
где  − непрерывная вектор функция такая, что
− непрерывная вектор функция такая, что  , назовем устойчивым по Красовскому, если существуют положительные числа
, назовем устойчивым по Красовскому, если существуют положительные числа  и
и  такие, что для любого решения
такие, что для любого решения  с начальными данными
с начальными данными  выполняется оценка
выполняется оценка
 ,
,
 − евклидова норма вектора
− евклидова норма вектора  ,
,  .
.
Отметим, что число  не зависит от выбора вектора
не зависит от выбора вектора  из шара
из шара  . В случае, если
. В случае, если  не зависит от выбора
не зависит от выбора  , говорят, что система (В.8) равномерно устойчива по Красовскому.
, говорят, что система (В.8) равномерно устойчива по Красовскому.
Кроме приведенных определений устойчивости используются и такие, как устойчивость по части переменных, на ограниченном интервале времени, абсолютная устойчивость, орбитальная устойчивость и другие.
Универсальным методом исследования устойчивости различных классов систем является второй метод Ляпунова [58, 59].
Пусть  (функция Ляпунова) непрерывно дифференцируема по обоим аргументам
(функция Ляпунова) непрерывно дифференцируема по обоим аргументам  и удовлетворяет условию
и удовлетворяет условию  Тогда производная функции Ляпунова в силу системы (В.8) равна
Тогда производная функции Ляпунова в силу системы (В.8) равна
 (В.9)
(В.9)
Приведем формулировки основных теорем.