ОПОРНЫЙ КОНСПЕКТ МУЛЬТИМЕДИЙНОГО КУРСА ЛЕКЦИЙ
ПО ФИЗИКЕ ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫОБУЧЕНИЯ
Лекция №1
МЕХАНИКА - это раздел физики, в котором изучается простейший вид движения материи- перемещения тел или частей тела друг относительно друга.
КЛАССИЧЕСКАЯ МЕХАНИКА изучает движение макроскопических тел (с размерами много большими размера атомов), которые движутся со скоростями, много меньшими скорости света.
РАЗДЕЛЫМЕХАНИКИ
КИНЕМАТИКА - изучает движение тел, не рассматривая причины его вызывающие.
ДИНАМИКА - изучает законы движения тел в связи с причинами, вызывающими это движение.
ЗАКОНЫСОХРАНЕНИЯ - являются наиболее общими физическими законами и связаны сзаконами сохранения энергии, импульса и момента импульса.
СТАТИКА - изучает законы равновесия тел.
ДВЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ В МЕХАНИКЕ
МАТЕРИАЛЬНАЯ ТОЧКА (М.Т.) - тело, форма и размеры которого несущественны в условиях данной задачи.
АБСОЛЮТНО ТВЕРДОЕ ТЕЛО (Т.Т.)- тело, деформацией размеров которого можно пренебречь.
СПОСОБЫОПИСАНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ТРАЕКТОРНЫЙ
ТРАЕКТОРИЯ – воображаемая линия в пространстве, вдоль которой движется материальная точка.
ХАРАКТЕРИСТИКА ДВИЖЕНИЯ S(t) – расстояние, проходимое М.Т. при движении вдоль траектории. ВЕКТОРНЫЙ
Положение М.Т. задается с помощью радиус -вектора, проведенного из точки, соответствующей началу отсчета, к материальной точке.
КООРДИНАТНЫЙ
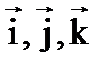Положение М.Т. можно описать в разнообразных системах координат – сферической, цилиндрической, полярной, но основной из них является ПРЯМОУГОЛЬНАЯ ДЕКАРТОВА СИСТЕМА КООРДИНАТ, которая представляет собой три взаимно перпендикулярных оси X, Y, Z, вдоль которых отложены единичные вектора или орты. Положение М.Т. в декартовой системе координат задается радиус- вектором r через проекции радиус-вектора на оси координат, выраженные в масштабе единичных векторов.
| r |
| X |
| Y |
| Z |
| x |
| y |
| z |
| i |
| j |
| k |
| r = xˑi + yˑj + zˑk |
ВИДЫМЕХАНИЧЕСКОГО ДВИЖЕНИЯ
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА – это движение, при котором отрезок прямой, соединяющей две любые точки твердого тела, остается параллельным самому себе.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ – это движение М.Т. по окружности.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА – это движение, при котором траектории всех точек тела являются окружностями, расположенными на одной прямой, называемой осью вращения. При этом ось вращения перпендикулярна плоскостям, в которых лежат траектории движения любой точки Т.Т.
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ – это движение, которое отличается той или иной степенью повторяемости. При этом тело совершает периодическое движение относительно своего равновесного положения.
КОМБИНИРОВАННОЕ ДВИЖЕНИЕ – это движение, при котором тело одновременно участвует в нескольких видах движения.
КИНЕМАТИКА
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ТРАЕКТОРИЯ – Воображаемая линия в пространстве, вдоль которой движется М.Т.
Часто положение М.Т. задается некоторым параметром, которым чаще всего является время t:
x(t), y(t), z(t) - это ПАРАМЕТРИЧЕСКАЯ ФОРМА ЗАДАНИЯ ДВИЖЕНИЯ.
Тогда уравнение траектории- это неявная функциональная зависимость между координатами М.Т., из которой исключено время – F (x,y,z)=0
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
СКОРОСТЬ 
–это векторная величина, характеризующая быстроту и направление перемещения материальной точки.
Быстрота перемещения М.Т. при равномерном и прямолинейном движении определяется отношением пути ΔS к интервалу времени Δt, за который этот путь пройден. V= ΔS/ Δt.
При неравномерном и криволинейном движении Δt→0 и тогда 
Вектор скорости всегда направлен по касательной к траектории.
ПЕРЕМЕЩЕНИЕ: 
– это вектор, соединяющий начальную и конечную точку пути.
ПУТЬ S – это расстояние, проходимое М.Т. вдоль траектории 
УСКОРЕНИЕ: 
- это векторная величина, характеризующая быстроту и направление изменения вектора скорости М.Т.
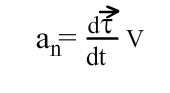
Тангенциальная и нормальная компоненты ускорения:
Лекция №2