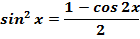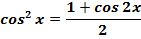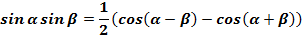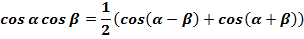Интеграл и его приложения.
Неопределённый интеграл.
П1. Понятие первообразной и неопределённого интеграла.
В теме 2 мы решали задачу нахождения производной или дифференциала некоторой функции. Часто необходимо по заданной производной или дифференциалу найти функцию, от которой была взята производная, то есть решить задачу, обратную задаче дифференцирования.
Нахождение функции по её производной рассматривается в интегральном исчислении.
Опр. Функция, восстанавливаемая по её производной или дифференциалу, называется первообразной.
Опр. Дифференцируемая функция 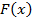 называется первообразной для функции
называется первообразной для функции 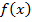 , если
, если 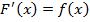 .
.
Например, найдем первообразную функции: 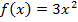 .
.
Решение:
Найдем функцию, производная от которой равна 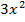
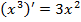 ⇒
⇒ 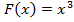 ,
,
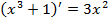 ⇒
⇒ 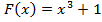 ,
,
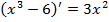 ⇒
⇒ 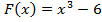 ,
,
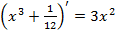 ⇒
⇒ 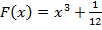 .
.
Зам. Функция, имеющая первообразную, имеет их бесконечное множество.
Т. Если функция 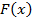 является первообразной для функции
является первообразной для функции 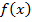 , то множество всех первообразных для функции
, то множество всех первообразных для функции 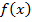 задаётся формулой
задаётся формулой 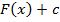 , где
, где 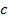 - произвольная константа.
- произвольная константа.
Опр. Совокупность всех первообразных для функции 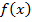 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 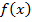 . При этом пишет
. При этом пишет 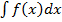 .
.
Этот символ читается «интеграл от эф от икс по дэ икс». Символ 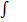 называется интегралом,
называется интегралом, 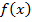 - подынтегральной функцией,
- подынтегральной функцией, 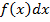 - подынтегральным выражением,
- подынтегральным выражением, 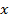 - переменной интегрирования.
- переменной интегрирования.
Итак, по определению
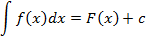
В примере выше 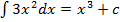 .
.
Опр. Нахождение функции по её производной или дифференциалу называется интегрированием.
п2. Свойства и таблица неопределённых интегралов.
Имеют место следующие свойства неопределённых интегралов:
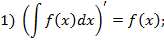
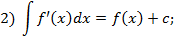
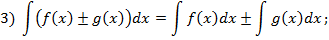
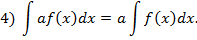
Зам. Формул для интеграла от произведения или частного функций, подобных формулам для производной, не существует!
|
|
Используя определение первообразной 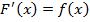 , определение неопределённого интеграла
, определение неопределённого интеграла 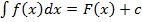 , и таблицу производных, можно получить таблицу неопределённых интегралов.
, и таблицу производных, можно получить таблицу неопределённых интегралов.
0. 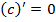 , значит
, значит 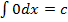 ;
;
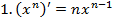 , значит
, значит 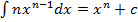 или
или 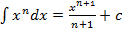 ;
;
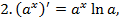 значит
значит 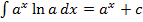 или
или 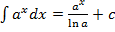 ;
;
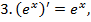 значит
значит 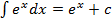 ;
;
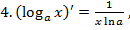 значит
значит 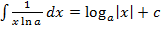 или
или 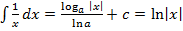 ;
;
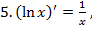 значит
значит 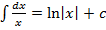 ,
, 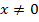 ;
;
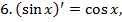 значит
значит 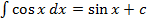 ;
;
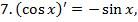 значит
значит 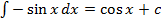 или
или 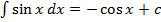 ;
;
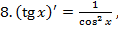 значит
значит 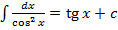 ;
;
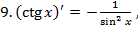 значит
значит 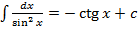 ;
;
Итак,
Таблица неопределённых интегралов.
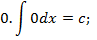

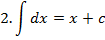
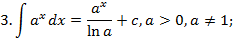
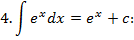
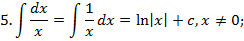
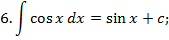
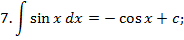
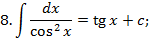
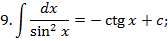

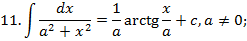
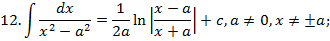
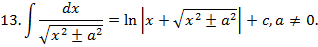
Зам. Оставим место ещё для 3 формул, которые мы получим позднее:
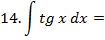
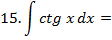
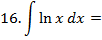
П3. Нахождение неопределенных интегралов непосредственным интегрированием.
Нахождение неопределённых интегралов с применением свойств и таблицы неопределённых интегралов, называется непосредственным интегрированием.
Пример. Найти интеграл: 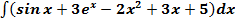 .
.
Решение:
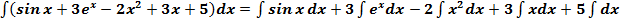 =
=
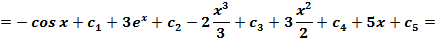
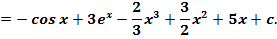
Ответ: 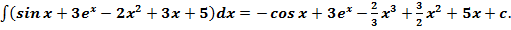
Задание 1. Найти интегралы:
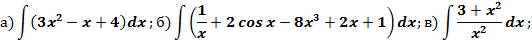
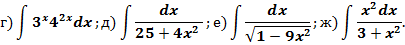
Домашнее задание.
Задание 1. Выучить определения первообразной и неопределённого интеграла, свойства и таблицу неопределённых интегралов.
Задание 2. Найти интегралы:
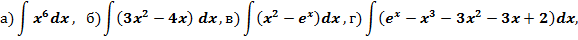
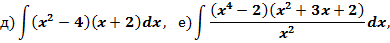

п4. Нахождение неопределенных интегралов методом подстановки.
В основе нахождения неопределённых интегралов методом подстановки лежит теорема, являющаяся следствием правила дифференцирования сложной функции:
Т. Пусть даны функции 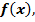
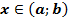 и
и 
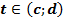 , и пусть существует сложная функция
, и пусть существует сложная функция 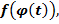
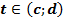 . Если функция
. Если функция 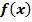 имеет первообразную
имеет первообразную 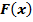 , а функция
, а функция 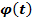 дифференцируема, то функция
дифференцируема, то функция 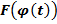 является первообразной для функции
является первообразной для функции 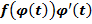 ,
, 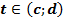 , и поэтому
, и поэтому
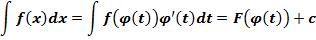
Пример. Найти интеграл 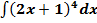 .
.
Решение:
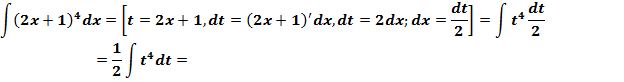
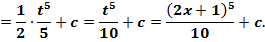
Ответ: 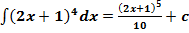
Задание. Найти интегралы:
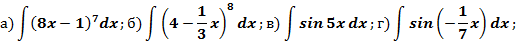
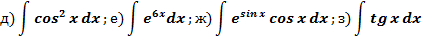
Зам. Итак, 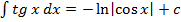
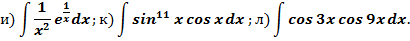
Указание. Для нахождения неопределенных интегралов используйте тригонометрические функции: