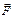Векторное произведение векторов, заданных своими декартовыми координатами

П. 7. Векторное произведение векторов

Определение. Тройкой векторов называется три вектора 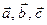с общим началом, перечисленных в определенном порядке ( 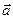- первый, 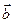- второй, 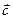- третий) и не лежащих в одной плоскости (некомпланарных).

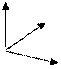
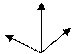
Определение. Тройка векторов называется «правой», если кратчайший поворот от вектора 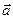к вектору 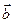, когда смотрим с конца вектора 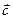, происходит против часовой стрелки. Если же этот поворот кажется происходящим по часовой стрелке, то тройка векторов называется «левой».

Происхождение названия: если векторы 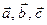совпадают соответственно с большим, указательным и средним пальцами правой руки – тройка правая, если левой руки – тройка левая.

Смысл декартовой тройки 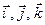всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.

 

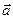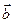Определение. Векторным произведением векторов и называется вектор 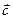, удовлетворяющий условиям:

1) 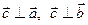, 2) , 3) 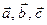образуют правую тройку. (1)

Обозначение 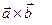или 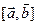. Это вектор.

 

Геометрический смысл векторного произведения

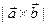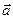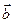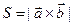Модуль векторного произведения равен площади параллелограмма, построенного на векторах и . . (2)

Механический смысл векторного произведения

1)

В

А

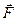Пусть сила приложена к точке В. Тогда моментом силы 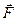относительно точки А называется вектор 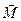такой, что , где вектор 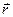- плечо АВ, .

 

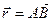2) Пусть материальная точка движется по окружности с центром в точке О,

M

O

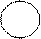
- линейная скорость движения точки, 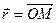- радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор 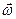такой, что .

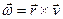Свойства векторного произведения.

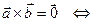
1. 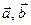– коллинеарные векторы. (3)

Доказательство.

Доказательство необходимости: 1) Пусть 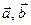– ненулевые векторы. Тогда длина векторного произведения 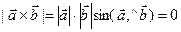тогда и только тогда, когда 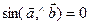, т.е. когда 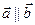. 2) Пусть среди векторов 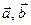может быть нулевой вектор (или оба нулевые). По определению 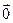-вектор можно считать параллельным любому вектору, т.е. пусть .

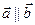Доказательство достаточности: 1) Пусть 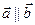, причем 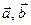– ненулевые векторы. Тогда длина векторного произведения 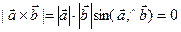, так как 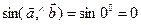. 2) Пусть 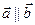, причем среди векторов 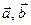может быть нулевой вектор (или оба нулевые). Тогда длина векторного произведения равна нулю, так как длина 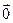- вектора равна 0. (что и треб. доказать).

Частный случай: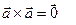

2. 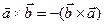(Пояснение: из-за смены троек)

3. Скалярный квадрат векторного произведения равен квадрату модуля векторного произведения: 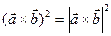(следует из 2-го свойства скалярного произведения)

4. Если 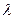– действительное число, то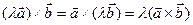

(Пояснение: если одну из сторон параллелограмма увеличить в λ раз, не меняя ее направление, то и площадь увеличиться в λ раз).

5. ,

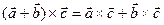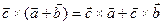
Перемножаем, строго соблюдая порядок.

6.

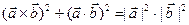
7.

 

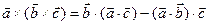
Таблица векторного умножения ортов

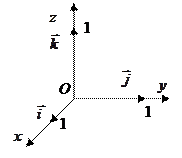Углы , , , , ,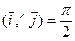

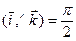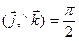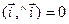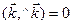; тогда 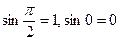; длины ортов равны .

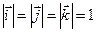Следовательно, исходя из определения векторного произведения, можем записать, что

, , ,

.

 

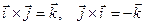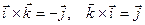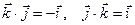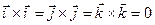Векторное произведение векторов, заданных своими декартовыми координатами

Два вектора и 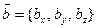заданы своими декартовыми координатами. Разложим их по ортам : , .

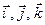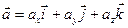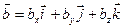Найдем векторное произведение данных векторов:

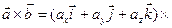
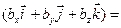
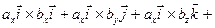
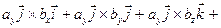
(воспользуемся таблицей векторного умножения ортов и сгруппируем) = = .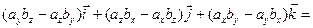

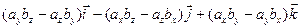Выражения в скобках получаются при вычислении определителей 2-го порядка, поэтому можно записать:

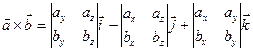–разложение по первой строке определителя 3-го порядка:

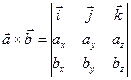– (4)

формула для нахождения векторного произведения векторов, заданных своими декартовыми координатами.

Можем записать, что координаты вектора векторного произведения равны:

.

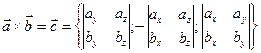Примеры.