Циркуляция векторного поля

Пусть в области задано непрерывное векторное поле и ориентированная гладкая кривая (с заданным направлением обхода). Обозначим единичный вектор касательной к линии через , направление которого совпадает с выбранным направлением на линии.

Определение. Линейным интегралом векторного поля вдоль линии называется криволинейный интеграл 1 рода от скалярного произведения векторов и :

,

где – дифференциал длины дуги кривой.

Если ввести в рассмотрение вектор (здесь – радиус вектор точки, описывающий линию ) и обозначить его проекции на координатные оси через , то предыдущую формулу можно записать в виде

,

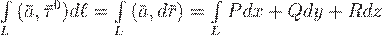где вектор направлен по касательной к . Правая часть последнего равенства является криволинейным интегралом 2 рода.

Если – силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии .

Определение. Линейный интеграл называется циркуляцией векторного поля , если – замкнутая линия.

Если – замкнутая пространственная кривая, то ее направление обхода специально оговаривается.

Пример. Вычислить циркуляцию векторного поля по замкнутой линии , состоящей из одного витка винтовой линии от точки до точки 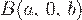и прямолинейного отрезка .
Решение.
Виток соответствует изменению параметра в уравнениях кривой от 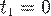до . Прямая имеет направляющий вектор , поэтому ее параметрические уравнения будут 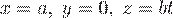, где изменяется от до . Вычислим циркуляцию как сумму криволинейных интегралов по дуге винтовой линии и по прямолинейному отрезку:


.
Ответ: .

Вопрос. Циркуляция векторного поля по замкнутому контуру 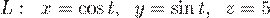, где , может быть вычислена по формуле:

 

Ротор

Определение. Если векторное поле имеет дифференцируемые в точке составляющие , то ротором (или вихрем) векторного поля в точке называется вектор

,

где частные производные вычислены в этой точке.

В символической форме имеет вид:

.

Поясним физический смысл ротора векторного поля. Рассмотрим векторное поле как поле скоростей движущейся жидкости. Поместим в таком потоке, в определенной его точке, бесконечно малое колесико с лопастями, расположенные по окружности этого колесика. Под воздействием потока жидкости такое колесико будет вращаться с некоторой скоростью, зависящей от направления оси колесика.

Выберем систему координат так, чтобы его ось колесика совпадала бы с осью . Найдем ротор поля линейных скоростей твердого тела, вращающегося вокруг оси с постоянной угловой скоростью , причем .

Тогда линейная скорость вращения тела будет равна:

,
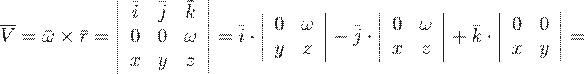
где – радиус вектор точки .
Тогда по определению ротора получим (здесь определитель раскрываем по первой строке):


.
С точностью до постоянного множителя ротор поля скоростей 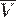представляет собой угловую скорость вращения твердого тела, т.е. он характеризует "вращательную компоненту" поля скоростей. С этим связано само название «ротор» (от латинского «вращатель»).

Направление ротора совпадает с направлением наибольшей плотности циркуляции.

Вопрос. Вторая координата ротора векторного поля равна
(введите с клавиатуры только число)

Ваш ответ

 

 

 

Формула Стокса

Если функции дифференцируемы в области и в этой области расположен некоторый замкнутый контур , то для любой незамкнутой поверхности 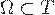, имеющей границу , имеет место формула Стокса:

,

где на берется та сторона, в точках которой вектор нормали направлен так, чтобы видимый с его конца обход контура совершался бы против часовой стрелки (ориентация поверхности согласована с обходом контура).

Формула Стокса позволяет свести вычисление циркуляции векторного поля по контуру к вычислению потока поля через незамкнутую поверхность , опирающуюся на контур (здесь – граница незамкнутой поверхности ). Заметим, что – любая поверхность, имеющая границей контур , поэтому возможен наиболее простой ее выбор.

Если через контур провести две поверхности и , то

.

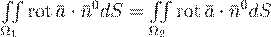Учитывая, что и ограничивают некоторую пространственное тело и, меняя направление нормали на поверхности на противоположное, т.е. на внешнее по отношению к , получим

,

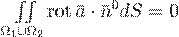т. е. поток вихря через замкнутую поверхность равен. Это означает, что поле вихря является соленоидальным.

Пример. Найти по формуле Стокса циркуляцию векторного поля по линии пересечения с координатными плоскостями той части поверхности , которая лежит в 1 октанте, т.е. .

Решение.
Находим ротор заданного векторного поля:

Пусть поверхностью с границей 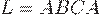является поверхность . Она является эллиптическим параболоидом и расположена в первом октанте.
Вычислим циркуляцию:
.

Нормаль к поверхности равна . Тогда единичная нормаль имеет координаты: . Откуда . В данном случае , т.к. в первом октанте. При этом скалярное произведение векторов и равно:
.

Отсюда по формуле получим:
.
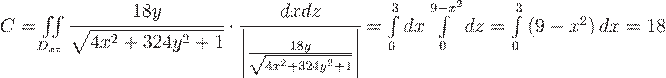Ответ: .

Вопрос. Используя формулу Стокса, циркуляцию векторного поля по линии пересечения параболоида с координатной плоскостью можно свести к вычислению интеграла:

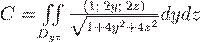
Виды векторных полей

Определение. Векторное поле называется соленоидальным в области , если его дивергенция равна нулю в каждой точке этой области .

Для соленоидального поля характерно, что в области отсутствуют источники и стоки, а поток для любой замкнутой поверхности , т.к. по теореме Остроградского-Гаусса .

 

Для соленоидальных полей имеет место закон сохранения интенсивности векторной трубки, состоящий в следующем.
Теорема. В соленоидальном поле поток вектора через поперечное сечение векторной трубки остается постоянным вдоль этой трубки.
Доказательство.
Пусть - соленоидальное поле, т.е. . Рассмотрим некоторую векторную трубку, т.е часть часть пространства ограниченную векторными линиями, пересекающими некоторый заданный контур. Пересечем векторную трубку двумя поперечными сечениями и . Эти сечения вместе с боковой поверхностью образуют замкнутую поверхность .

Т.к. поле соленоидально, то поток через замкнутую поверхность равен нулю: 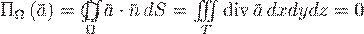. Поэтому получим:

.

На боковой поверхности вектор направлен по касательной к векторной линии, т.е. лежит в касательной плоскости. Поэтому перпендикулярен вектору нормали к поверхности , т.е. , откуда .
На поверхностях и направления нормалей берутся внешними к поверхностям. На поверхности (см. рисунок) внешняя нормаль направлена в сторону, противоположному направлению векторных линий. Поэтому заменив ее на внутреннюю нормаль и, соответственно, поменяв ориентацию , будем иметь:

.

Поэтому поток соленоидального поля через любое поперечное сечение векторной трубки имеет одно и тоже значение. Иногда соленоидальное поле назвают трубчатым.
Это согласуется с физическими моделями соленоидальных полей, когда говорят, что поле несжимаемо, что через поперечное сечение трубки проходит одинаковое количество векторных линий. Т.е. векторные линии не возникают и не пропадают ни в какой точке поля. Они либо уходят в бесконечность, либо являются замкнутыми.

Пример 1. Поле напряженности магнитного поля, образованного электрическим током, текущему по бесконечному прямолинейному проводу, соленоидально всюду, кроме точек оси , т.к. .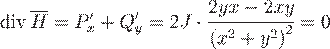

Пример 2. Поле электрической напряженности точечного заряда также соленоидально всюду, за исключением начала координат.

Определение. Векторное поле называется безвихревым в области , если в каждой ее точке .

Определение. Векторное поле , заданное в области , называется потенциальным, если в этой области существует такая скалярная функция , что вектор можно представить в виде градиента этой функции:

.

Функция называется потенциальной функцией или потенциалом векторного поля .

Из формулы следует, что

и ,

т. е. – есть полный дифференциал потенциала этого поля. Критерием потенциальности векторного поля служит равенство

.

Следовательно, для того чтобы ВП было потенциальным необходимо и достаточно, чтобы оно было безвихревым.
Выполнение условия в области приводит не только к потенциальности ВП, но и к следующим результатам:
а) в области существует потенциал , который может быть определен с точностью до постоянной по формуле

где 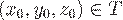– любая фиксированная точка; 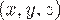– переменная точка в области ; – произвольная постоянная. Во втором интеграле формулы постоянен , а в третьем и постоянные величины;

б) циркуляция векторного поля по любому замкнутому контуру равна нулю:

.

Если же хотя бы в одной точке, внутренней по отношению к контуру , поле не определено, циркуляция по этому контуру может и не обратиться в нуль, хотя поле потенциально;

в) для любых двух точек и области значение линейного интеграла векторного поля

не зависит от пути интегрирования в области ;

г) линейный интеграл этого поля вдоль любого контура , соединяющего точки и равен разности значений потенциала в конечной и начальной точках контура:

.

Физический смысл этого результата: если – силовое поле, то разность потенциалов между точками и равна работе, которую поле совершает при перемещении материальной точки из в .

Пример 3. Доказать, что векторное поле является потенциальным. Найти его потенциал и вычислить линейный интеграл поля от точки до точки .
Решение.
Так как поле определено и дифференцируемо в любой точке пространства и (проверьте самостоятельно), то данное поле потенциально. Найдем потенциал поля, взяв в качестве точки 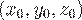начало координат:

.

Вычислим линейный интеграл:
.

Определение. Векторное поле называется гармоническим, если оно одновременно является и потенциальным и соленоидальным, т.е. и .

Из определения следует, что гармоническое поле одновременно является полем безвихревым и без источников и стоков. Потенциал этого поля удовлетворяет условию: .

Пример 4. Выяснить тип векторного поля .
Решение.
Найдем ротор векторного поля :
.

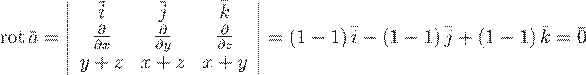Рассчитаем дивергенцию векторного поля :

Следовательно, поле – гармоническое.

Существует теорема Гельмгольца о разложении произвольного поля на две компоненты - потенциальную и соленоидальную.

Теорема. Если дивергенция и ротор векторного поля определены в каждой точке области пространства, то всюду в функция может быть представлена в виде суммы безвихревого (потенуиального) поля и соленоидального поля :

,

где и для всех точек области .

Замечание. Для описания электромагнитных полей существуют система уравнений Максвелла, накопленных к середине XIX века на основе экспериментальных результатов.
1) , т.е. электрический ток и изменение электрической индукции порождают вихревое магнитное поле.
2) , т.е. изменение магнитной индукции порождает вихревое электрическое поле.
3) , т.е. электрический заряд является источником электрической индукции.
4) 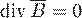, т.е. магнитных зарядов не существует.

Вопрос. Поле 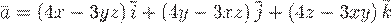является

Гармоническим

Недостаточно данных для ответа

Соленоидальным

Произвольным

Потенциальным