ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Пусть  - непрерывная функция и
- непрерывная функция и  - гладкая поверхность
- гладкая поверхность  , где
, где  задана в некоторой области
задана в некоторой области  плоскости
плоскости  . Поверхностным интегралом I рода называется предел интегральной суммы при условии, что
. Поверхностным интегралом I рода называется предел интегральной суммы при условии, что  :
:
 ,
,
где  - площадь
- площадь  -го элемента поверхности
-го элемента поверхности  , точка
, точка  принадлежит этому элементу,
принадлежит этому элементу,  - диаметр этого элемента,
- диаметр этого элемента,  определена в каждой точке поверхности
определена в каждой точке поверхности  .
.
Значение этого интеграла не зависит от выбора стороны поверхности  , по которой производится интегрирование.
, по которой производится интегрирование.
Поверхностный интеграл I рода вычисляется по формуле
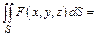

Рассмотрим двустороннюю поверхность  и выберем
и выберем
на ней определенную сторону  . Функция
. Функция  определена в точках данной поверхности. Предел интегральной суммы
определена в точках данной поверхности. Предел интегральной суммы  , где
, где  - проекция на плоскость
- проекция на плоскость 
 -го элемента поверхности
-го элемента поверхности  , имеющего площадь
, имеющего площадь  , при условии
, при условии  называется поверхностным интегралом II рода, распространенным на выбранную сторону поверхности
называется поверхностным интегралом II рода, распространенным на выбранную сторону поверхности  , и обозначается символом
, и обозначается символом
 .
.
Если  ,
,  ,
,  - непрерывные функции и
- непрерывные функции и  - сторона гладкой поверхности
- сторона гладкой поверхности  , характеризуемая направлением нормали
, характеризуемая направлением нормали  , то соответствующий поверхностный интеграл II рода выражается так:
, то соответствующий поверхностный интеграл II рода выражается так: 
 .
.
При переходе на другую сторону  поверхности этот интеграл меняет знак на противоположный.
поверхности этот интеграл меняет знак на противоположный.
Если поверхность  задана уравнением в неявном виде
задана уравнением в неявном виде  , то направляющие косинусы нормали этой поверхности определяются по формулам
, то направляющие косинусы нормали этой поверхности определяются по формулам
 ,
,  ,
,
 ,
,
где знак перед радикалом должен быть согласован со стороной поверхности.
ЭЛЕМЕНТЫТЕОРИИ ПОЛЯ
Скалярное поле
Определение. Скалярное поле определяется скалярной функцией точки  , где
, где  - точка пространства,
- точка пространства,  - ее радиус вектор.
- ее радиус вектор.
Поверхности уровня  - const.
- const.
Линии уровня плоского скалярного поля  - const.
- const.
Оператор Гамильтона (линейный дифференциальный
оператор  (набла)):
(набла)):  .
.
Градиент. Градиент скалярного поля – вектор  ,
,  .
.
Свойства градиента
 ,
,  ,
,  ,
,  ,
,  ,
, 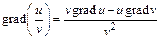 ,
,
 ,
,
 ,
,
 .
.
Градиент скалярного поля в цилиндрических координатах 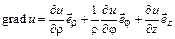 .
.
Градиент скалярного поля в сферических координатах
 .
.
Производная скалярного поля  по направлению
по направлению

 ,
,  ,
,  .
.
.  , если
, если  имеет направление
имеет направление  .
.
Векторное поле
Определение. Векторное поле определяется векторной функцией точки 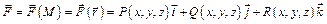 где
где  - точка пространства;
- точка пространства;  - ее радиус-вектор.
- ее радиус-вектор.
Векторная линия (силовая линия, линия тока) поля – решение системы  .
.
Дивергенция (расходимость) векторного поля
 .
.
Свойства дивергенции
 ,
,  ,
,  ,
,
 ,
,
 ,
, 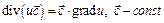 ,
,
Дивергенция векторного поля в цилиндрических координатах  .
.
Дивергенция векторного поля в сферических координатах

Ротор (вихрь) векторного поля

или в символическом виде
 .
.
Свойства ротора
 ,
,  ,
,  ,
,  ,
,  .
.
Поток векторного поля  через поверхность
через поверхность  в сторону, определяемую единичным вектором нормали
в сторону, определяемую единичным вектором нормали  ,
,


 ,
,
где  - величина проекции вектора
- величина проекции вектора  на направление вектора
на направление вектора  .
.
Если поверхность  задана уравнением
задана уравнением 
 , поток через верхнюю сторону поверхности можно вычислить по формуле
, поток через верхнюю сторону поверхности можно вычислить по формуле


Если уравнение поверхности  есть
есть  ,
,  , то
, то
 .
.
Линейный интеграл от вектора  по линии
по линии 
 ,
,
где  - проекция вектора
- проекция вектора  на касательную к
на касательную к  . Линейный интеграл выражает работу векторного поля
. Линейный интеграл выражает работу векторного поля  вдоль линии
вдоль линии  .
.
Циркуляция векторного поля  вдоль контура
вдоль контура  - линейный интеграл вдоль замкнутой линии
- линейный интеграл вдоль замкнутой линии 
 .
.
Формула Стокса


или в векторной форме  ,
,
где  - единичный вектор нормали к поверхности
- единичный вектор нормали к поверхности  , направление которого таково, что при обходе контура
, направление которого таково, что при обходе контура  поверхность
поверхность  остается слева.
остается слева.
Формула Остроградского


или в векторной форме  ,
,
где  - внешняя сторона поверхности, ограничивающей тело
- внешняя сторона поверхности, ограничивающей тело  ;
;  - единичный вектор внешней нормали к ней.
- единичный вектор внешней нормали к ней.
Векторное поле  - потенциальное, если
- потенциальное, если  . Функция
. Функция  называется потенциалом векторного поля
называется потенциалом векторного поля  . Поле
. Поле  потенциально в поверхностно односвязной области тогда и только тогда, когда
потенциально в поверхностно односвязной области тогда и только тогда, когда  или
или 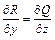 ,
,  . Потенциал в этом случае можно найти по формуле
. Потенциал в этом случае можно найти по формуле

 .
.
Векторное поле  называется соленоидальным, если
называется соленоидальным, если  .
.
Оператор Лапласа  .
.
Оператор Лапласав цилиндрических координатах
 .
.
Оператор Лапласав сферических координатах
 .
.
 .
.
Уравнение Лапласа  .
.
Функции, удовлетворяющие уравнению Лапласа, называются гармоническими.
Операции второго порядка
 ,
, 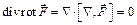 ,
,
 ,
, 
 ,
, 
 ,
,
где  .
.