Пусть в первых k-1 испытаниях событие А не наступало, а в k-ом испытании появилось. Вероятность этого события .
Свойства функции распределения.
Свойство 1. Функция распределения F(x)–неубывающая функция, т.е. для  таких что x1<x2 таких что x1<x2 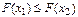 . .
Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е.  , представим в виде объединения двух несовместимых событий , представим в виде объединения двух несовместимых событий
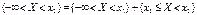 . .
Тогда по теореме сложения вероятностей получим
 , т.е. , т.е.
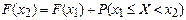 . Поскольку . Поскольку  , то , то
 . .
Свойство 2. Для любых 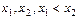 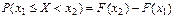
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.
Свойство 3.  , ,  . .
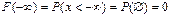 , , 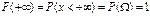 . .
Свойство 4. Функция F(x) непрерывна слева. (т.е.  ). ).
Свойство 5. Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
 . .
Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий. 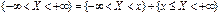 . Найдем их вероятности . Найдем их вероятности
 . .
Поскольку вероятность достоверного события равна единице, то
 . Отсюда . Отсюда 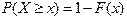 . .
| 14.Дискретные случайные величины. Закон распределения. Биноминальное,
геометрическоеираспределениеПуассона.
o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно.
o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е. 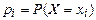 , причем , причем  .
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. .
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
| X
| x1
| x2
| …
| xn
| …
| | P
| p1
| p2
| …
| pn
| …
| Такая таблица называется рядом распределения дискретной случайной величины.
 Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины. Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины.
Пример. Рассмотрим следующую дискретную случайную величину
o Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения  с вероятностями с вероятностями  . .
Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения с вероятностями.
X 0 1 … k …
P
Обозначают, т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0<p<1) и, следовательно, вероятность его не появления q=1-p. Испытания заканчиваются как только появится событие А. Таким образом, если событие А появилось в k-ом испытании, то в предшествующих k-1 испытаниях оно не появлялось.
Обозначим через X дискретную случайную величину—число испытаний, которое нужно провести до первого появления события А. Очевидно, возможными значениями случайной величины Х являются натуральные числа.
Пусть в первых k-1 испытаниях событие А не наступало, а в k-ом испытании появилось. Вероятность этого события.
o Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения с вероятностями, где q=1-p. X 1 2 3 … k …
P p qp q2p … qk-1p …
Очевидно, что вероятности появления значений 1,2,3… образуют геометрическую прогрессию с первым членом р и знаменателем q (0<q<1).
.При бросании монеты «герб» может появится либо 2, либо 1, либо 0 раз. Т.е. возможные значения Х таковы: х1=0,х2=1, х3=2.
Найдем вероятности этих возможных значений по формуле Бернулли:
 ; ;
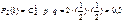 ; ;
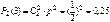 . .
|
|
 таких что x1<x2
таких что x1<x2 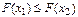 .
. , представим в виде объединения двух несовместимых событий
, представим в виде объединения двух несовместимых событий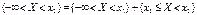 .
. , т.е.
, т.е.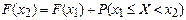 . Поскольку
. Поскольку  , то
, то .
.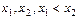
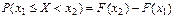
 ,
,  .
.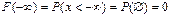 ,
, 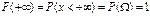 .
. ).
). .
.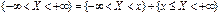 . Найдем их вероятности
. Найдем их вероятности .
. . Отсюда
. Отсюда 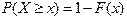 .
.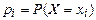 , причем
, причем  .
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
.
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
 Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины.
Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины. с вероятностями
с вероятностями  .
.


 ;
;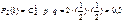 ;
;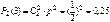 .
.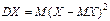 . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
o Средним квадратическим отклонением случайной величины Х называется число
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
o Средним квадратическим отклонением случайной величины Х называется число  .
.
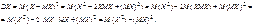 Ряд распределения случайной величины Х2
Ряд распределения случайной величины Х2
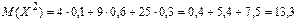
 .
.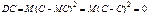 .
.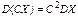 .
. .
.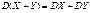 .
.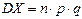 .
. , где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
, где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных. .Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события
.Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события  . По свойству 4:
. По свойству 4: 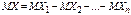 .Согласно примеру 2
.Согласно примеру 2  . Таким образом, получим
. Таким образом, получим  .
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании:
.
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: 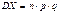 .
Случайная величина Х—число появлений события А в n независимых испытаниях.
.
Случайная величина Х—число появлений события А в n независимых испытаниях.  , где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
, где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
 .
.
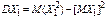 . Т.к. MX1=p.
. Т.к. MX1=p.  , то
, то  . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда
. Очевидно, что дисперсия остальных случайных величин также равна pq, откуда  .
Начальным моментом порядка к случайным величинам Хназывают математическое ожидание случайной величины Хk:
.
Начальным моментом порядка к случайным величинам Хназывают математическое ожидание случайной величины Хk:
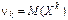 . В частности,
. В частности,  ,
,  .
Пользуясь этими моментами, формулу для вычисления дисперсии
.
Пользуясь этими моментами, формулу для вычисления дисперсии 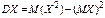 можно записать так:
можно записать так:  .
Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х-ХМ.
o Центральным моментом порядка kслучайной величины Х называют математическое ожидание величины (Х-МХ)k.
.
Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х-ХМ.
o Центральным моментом порядка kслучайной величины Х называют математическое ожидание величины (Х-МХ)k.
 . В частности
. В частности
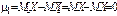 ,
,  . Следовательно,
. Следовательно,  .
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:
.
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:  .
.  .
Моменты более высоких порядков применяются редко. Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
.
Моменты более высоких порядков применяются редко. Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.