Задание по дисциплине «Математика» для студентов группы МР-11 на 19.03.2020 (1 пара)
Тема: Предел функции. Непрерывные функции.
Литература:
Алимов Ш.А., Колягин Ю.М.:«Алгебра и начала математического анализа.10-11 классы. 10-11 классы» -М.:Просвещение,2011.
План работы:
- Изучить приложенный материал по теме. Выписать определение предела функции, свойства пределов, определение функции, непрерывной в точке и на промежутке.
- Подписать свою работу.
- отправить работу в виде личного сообщения в сети ВКонтакте (Дина Соколова) до 12.00, 20.03.2020
Материал для самостоятельного изучения.
Понятие «бесконечность» используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел.
Бесконечность – сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость, то ось абсцисс(ординат) уходит на бесконечность, если ее безгранично продолжать влево или вправо (вниз или вверх).
Теперь давайте перейдем к пределу функции на плюс и минус бесконечности.
Предел функции на плюс бесконечности.
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:


Предел функции на минус бесконечности.
Посмотрим немного другой случай:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:


Предел функции на бесконечности.
Так же наши соотношения могут выполняться одновременно:

Тогда принято записывать как: 
Для вычисления предела на бесконечности пользуются несколькими утверждениями.
Основные свойства:
1. Для любого натурально числа m справедливо следующее соотношение:

Если  и
и 
а) Предел суммы равен сумме пределов:

б) Предел произведения равен произведению пределов:

в) Предел частного равен частному пределов:
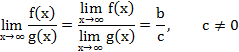
г) Постоянный множитель можно вынести за знак предела:
Функция непрерывна, то она удовлетворяет условию  И функцию f (x) называют непрерывной в точке х = а.
И функцию f (x) называют непрерывной в точке х = а.
Иными словами, функцию y = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.
Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.
При изучении различных функций (линейной, квадратичной, степенной, иррациональной, тригонометрических) мы отмечали, что они являются непрерывными либо на всей числовой прямой, либо на промежутке. Исходя из этого, можно сформулировать следующее утверждение: если выражение f (x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция y = f (x) непрерывна в любой точке, в которой определено выражение f (x).
Пример. Вычислить: 
Решение:
выражение х3 – 2х2 + 5х +3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х3 – 2х2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем:
 .
.
Ответ: 7.