Решение плоской задачи теории упругости в напряжениях
Методические указания
При решении задачи в напряжениях основными неизвестными будут σx, σy, σz. Если объёмные силы постоянны, то уравнения для обеих плоских задач совпадают. Решение упрощается, если все неизвестные напряжения выразить через одну функцияю φ (х, у) – функцию напряжений следующим образом

где X, Y – объёмные силы, соответственно параллельные осям х и у.
Функцию φ (х, у) находим из решения бигармонического уравнения

при граничных условиях


Выражение (2.2) представляет собой функцию Эри.
При определении значения угла между нормалью и осью, поворачиваем нормаль против хода часовой стрелки до совмещения с положительным направлением взятой оси.
Задание
Дано: прямоугольная пластина (рис. 2.2), толщиной равной единице.

Требуется:
1. Проверить, можно ли взятую функцию φ(х, у) принять для решения плоской задачи;
2. Найти выражения для напряжений;
3. Построить эпюры напряжений для сечений: а) сечение с нормалью х – эпюры σх, τух; б) сечение с нормалью у – эпюры σу, τху;
4. Определить поверхностные силы X ν, Y ν на всех четырёх гранях пластины. Построить их эпюры с указанием направления сил.
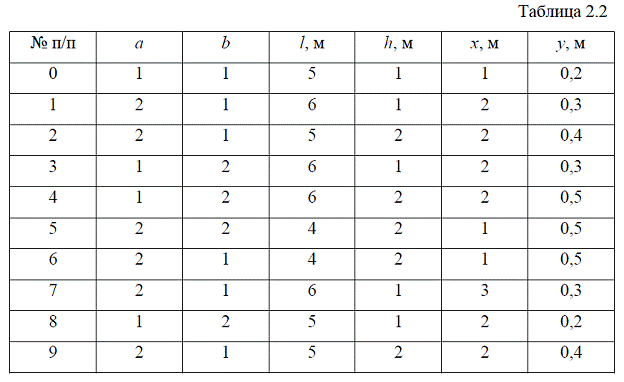
Выражение для функции φ (х, у) взять из таблицы 2.1(по последней), а числовые значения – из таблицы 2.2(по первой), согласно двух последних цифр шифра. Объёмными силами пренебречь.

Пример
Дано:

a = 1; b = 2; h = 2 м; l = 5 м; x = 1 м; y = 0,2м.
Решение.
С учётом чисел запишем:

1. Проверяем пригодность φ (х, у) для решения задачи. Взятая функция может быть решением задачи, если она обращает бигармоническое уравнение (2.2) в тождество. Находим производные

Подставим четвёртые производные из (2.5) в уравнение (2.2):
0 + 2∙0+0 = 0.
Получили, что функцию (2.4) можно взять для решения задачи.
2. Находим напряжения. Учтём, что X = 0; Y = 0.
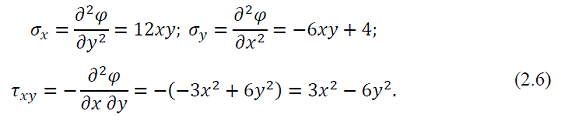
3. Строим эпюры напряжений.
а) сечение х = 1. σ х = 12∙1∙ у (уравнение прямой линии).
При у = ± 1, σ х = ± 12.
τух = 3∙(1)2 – 6 у 2 = 3 – 6 у 2 (уравнение квадратичной параболы).
При у = 0, τух = 3; при у = ± 1, τух = - 3.
Найдём значения у, при которых τух = 0.
3 – 6у2 = 0;

б) сечение у = 0,2.
σу = - 6 х ∙0,2+4 = - 1,2 х + 4 (прямая линия).
При х = 0, σу = 4; при х = 5, σу = -1,2∙5 + 4 = -2.
τху = 3 х 2 - 6∙(0,2)2 = 3 х 2 – 0,24 (квадратичная парабола).
При х = 0, τху= - 0,24; при х = 5, τху = 3∙(5)2 – 0,24 = 74,76.
Найдём значения х, при котором τху = 0.

Результаты вычислений представлены на рис. 2.3.

4. Определяем поверхностные силы по формуле (2.3).
Левая грань. Её уравнение: х = 0. Проведём к ней внешнюю нормаль v. Для определения значения угла между нормалью и осью координат поворачиваем нормаль против хода часовой стрелки до совмещения с положительным направлением взятой оси. Находим:
l = cos(x, v) = cos(180°) = - 1; m = cos(y, v) = cos(270°) = 0.
Xv = σx l + τxy m = 12∙0∙ y ∙(-1) + τxy∙0 = 0.
На этой грани сил, параллельных оси х, нет.
Yv = σy m + τxy l = σy∙0 + (3∙0 – 6 y 2)(- 1) = 6 y 2
- квадратичная парабола.
При у = ± 1, Yv = 6; при у = ± 0,5, Y v= 1,5; при у = 0, Yv = 0.
Правая грань: х = 5; l = cos(0°) = 1; m = cos(90°) = 0.
Xv = 12∙5 y – τxy∙0 = 60 y – прямая линия.
При у = ± 1, Xv = 60; Yv = σу∙0 + (3∙52– 6 у 2) = 75 – 6 у 2.
При у = 0, Xv = 75; при у = ± 1, Yv = 75 - 6∙(1)2 = 69.
Верхняя грань: у = 1; l = cos(270°) = 0; m = cos(0°) = 1.
Xv = σx∙0 + (3 x 2- 6∙12)∙(1) = 3 x 2– 6 – квадратичная парабола.
При х = 0, Xv = - 6; при х = 5, Xv = 3∙52– 6 = 69.
Найдём значения х, при котором Yv = 0
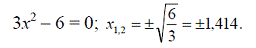
Yv = (- 6 x ∙1 + 4)∙(1) + τyx∙0 = - 6 x + 4 – прямая линия.
При х = 0, Yv = 4; при х = 5, Yv = - 6∙5 + 4 = - 26.
Нижняя грань: y = - 1; l = cos(90°) = 0; m = cos(180°) = - 1.
Xv = σx∙0 + [3 x 2 – 6(- 1)2](- 1) = 6 – 3 x 2– квадратичная парабола.
При х = 0, Xv = 6; при х = 5, Xv = = - 69.
Определим значение х, при котором Xv = 0

Yv = [- 6 x (-1) + 4](- 1) + τyx∙0 = - 6 x – 4 – прямая линия.
При х = 0, Yv = - 4; при х = 5, Yv = - 34.
Строим эпюры (рис. 2.4).
Проверка:
1. У сил, касательных к поверхностям граней, должен выполняться закон парности касательных напряжений.
2. В точках пересечения граней они имеют равные значения и направлены к этой точке или от неё.

Расчёт прямоугольной пластины
Методические указания
Конструкционный элемент, у которого толщина h мала по сравнению с размерами в плане, есть пластина (рис. 2.1).

Она будет тонкой, если 1/5 ≥ h / b ≥ 1/180. Плоскость, делящая толщину h пополам, называется срединной. В соединениях края пластины имеют различные закрепления. Наложенные связи, препятствующие линейным и угловым перемещениям, могут быть абсолютно жёсткими или упругими.
От действия поверхностных сил, параллельных оси Z, пластина изгибается. При этом её точки получают перемещения U, V, W – соответственно вдоль осей X, Y, Z. Перемещение W называют прогибом.
Усилия и моменты в пластинках принято относить к единице длины того сечения, в котором они действуют. Эти погонные усилия измеряют в ньютонах на метр (Н/м), а погонные моменты – в ньютон-метр и на метр (Н∙м/м).
Техническая теория расчёта пластин основана на следующих гипотезах:
1. Прямолинейный элемент, перпендикулярный к срединной плоскости пластины до её изгиба, остаётся прямым и перпендикулярным к срединной плоскости после изгиба пластины и не меняет своей длины.
Упрощения:
Упрощения: а) угловые деформации γzx = 0, γzy = 0 из-за неизменяемости прямого угла;
б) относительная линейная деформация εz = 0, так не меняется длина прямолинейного элемента. Тогда

Отсюдаw=∮(x,y) то есть прогиб не зависит от переменной z. Поэтому прогибы можно определять только в точках срединной плоскости. Следовательно, срединная плоскость есть расчётная схема пластины.
2. Слои пластины, параллельные срединной плоскости, не оказывают взаимного давления в направлении оси z, т. е. σz = 0.
3. Срединная плоскость не имеет деформаций растяжения, сжатия и сдвига. Перемещения её точек вдоль осей Х и Y равны нулю: U 0 = 0; V 0 = 0.
На основе гипотез технической теории расчёта пластин получим, что все неизвестные перемещения U, V; деформации ξх, ξу, γху; напряжения σx, σy, τxy, τzy, τzx будут выражены через прогиб – W (x, y). Его находим из решения дифференциального уравнения равновесия пластины при изгибе (уравнение Софи Жермен):
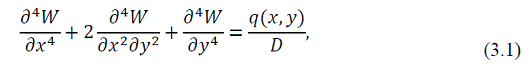
где

цилиндрическая жёсткость поперечного сечения пластины.
Внутренние силы (статический эквивалент напряжений) определяем по формулам:
а) интенсивность изгибающих моментов в поперечных сечениях с нормалями х и у соответственно:

б) интенсивность поперечных сил:

в) интенсивность крутящего момента:

При решении уравнения (3.1) постоянные интегрирования находим из граничных условий. Граничные условия – это аналитические выражения для кинематических и статических параметров в краевых точках. Различают такие группы граничных условий:
1. Кинематическая – известны прогибы и углы поворота сечений:
а) сечение с нормалью х: 
б) сечение с нормалью у: 
2. Статическая – известны внутренние силы:
а) сечение с нормалью х: Мх, Qх, H;
б) сечение с нормалью у: Му, Qу, H.
3. Смешанная – известны часть перемещений и внутренних сил.
Запишем граничные условия для всех краёв срединной плоскости пластины:
1. При х = 0, W = 0
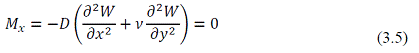
- смешанная группа;
2. При х = а, W = 0 
- смешанная группа;
3. При y = b, My = 0

- кинематическая группа;
4. При y = b, My = 0

- статическая группа,
где - Qу интенсивность приведенной поперечной силы.
Задание
Дано: прямоугольная пластина (рис. 3.1)

Требуется:
1. Выяснить вид закрепления краёв пластины;
2. Определить постоянную С;
3. Записать выражения для внутренних сил;
4. Построить эпюры внутренних сил в одном из сечений: сечение х – эпюры Mx, Qx; сечение у - эпюры Mу, Qу.
D, C, q 0 – постоянные. q0определить из условия прочости
Выражение для функции q (х, у) и W (x, y) взять из таблицы 3.1, а числовые значения – из таблицы 3.2 согласно двухзначного шифра, выданного преподавателем.
Таблица 3.1
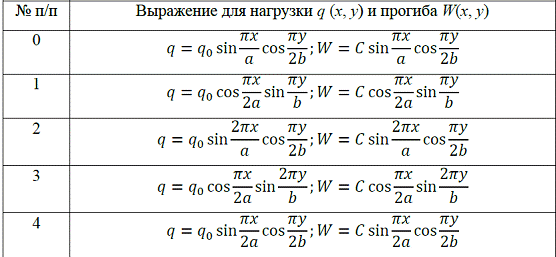

Пример
Дано:

а = 4м; b = 3м; h = 0,2м; х = 1м; у = 1м; ν = 0,2.
 – условие прочности
– условие прочности
Решение.
1. Выясним вид закрепления краёв пластины.
а) Проверяем граничное условие W = 0.
При х = ± а

т.е. вертикальная опора есть.
При y = ± b
 т.е. вертикальной опоры нет.
т.е. вертикальной опоры нет.
б) Проверяем углы поворота граней

При х = ± а
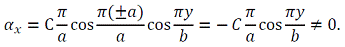
Эти края шарнирно закреплены (свободно опёрты).
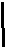


При y = ± b
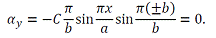
Края имеют подвижное (в направлении оси z) защемление.
1. Для определения постоянной С возьмём уравнение (3.1). Находим:
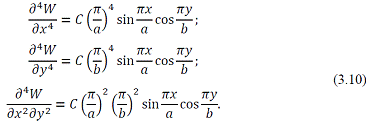
Формулы (3.9) и (3.10) подставим в уравнение (3.1):

Получим
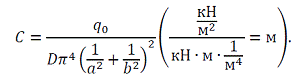
1. Выражение для внутренних сил. Необходимые производные:
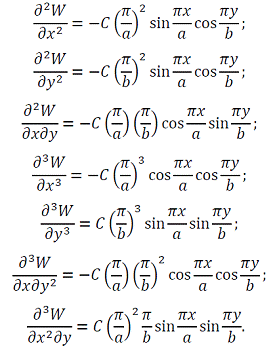
По формулам (3.2-3.4) имеем:
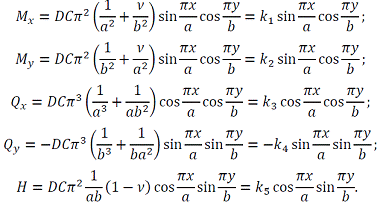
2. Построение эпюр внутренних сил (рис. 3.2).
а) Сечение х = 1м:

Находим:

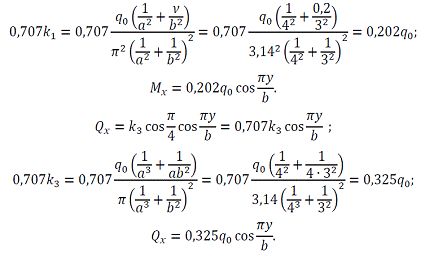
б) Сечение у = 1м:

Величины внутренних сил при различных значениях х и у даны в таблице 3.3.
