ЛЕКЦИЯ 1 ФАКТОРИАЛ, ПЕРЕСТАНОВКИ
Комбинаторика – это, как и намекает само название, раздел математики, изучающий различные наборы или комбинации каких-либо объектов (элементов) – чисел, предметов, букв в словах и прочего. Очень интересный раздел.) Но по тем или иным причинам сложный для восприятия. Почему? Потому, что в нём сплошь и рядом фигурируют более сложные для визуального восприятия термины и обозначения. Если символы 10, 2, 3/4 и даже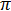 
, 
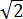или log25 нам визуально понятны, т.е. мы можем их как-то «пощупать», то с обозначениями типа 15!, P9, 
, 
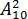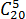начинаются проблемы. Кроме того, в большинстве учебников эта тема излагается довольно сухо и затруднительно для восприятия. Надеюсь, данный материал хотя бы немного поможет решить эти проблемы, и комбинаторика вам понравится.
С комбинаторными задачами ежедневно сталкивается каждый из нас. Когда утром мы принимаем решение, как одеться, мы комбинируем те или иные виды одежды. Когда готовим салат, мы комбинируем ингредиенты. От того, какая комбинация продуктов выбрана, зависит результат – вкусно или невкусно. Правда, вопросами вкуса занимается уже не математика, а кулинария, но тем не менее.) Когда, играем «в слова», составляя маленькие словечки из одного длинного, мы комбинируем буквы. Когда открываем кодовый замок или набираем номер телефона, то комбинируем цифры.) Завуч школы составляет расписания уроков, комбинируя предметы. Футбольные команды на Чемпионате Мира или Европы распределяют по группам, образуя комбинации. И так далее.
Комбинаторные задачи люди решали ещё в глубокой древности (магические квадраты, шахматы), а настоящий расцвет комбинаторики пришёлся на VI–VII века, во время широкого распространения азартных игр (карты, игральные кости), когда игрокам приходилось продумывать различные ходы и тем самым фактически также решать комбинаторные задачи.) Вместе с комбинаторикой в это же время зародился и другой раздел математики – теория вероятностей. Эти два раздела – очень близкие родственники и идут рука об руку. И при изучении теории вероятностей мы не раз будем сталкиваться с задачами комбинаторики.
|
|
И начнём мы изучение комбинаторики с такого краеугольного понятия, как факториал.
Что такое факториал?
Красивое слово «факториал», но многих пугает и ставит в тупик. В настоящем уроке мы разберёмся и хорошенько поработаем с этим несложным понятием. Это слово происходит от латинского «factorialis», что означает «умножающий». И неспроста: в основе вычисления любого факториала стоит обыкновенное умножение. Итак, что же такое факториал.
Возьмём какое-нибудь натуральное число n. Совершенно произвольное: хотим 2, хотим 10, - какое угодно, лишь бы натуральное. Так вот, факториал натурального числа n – это произведение всех натуральных чисел от 1 до n включительно. Обозначается вот так: n! То есть,
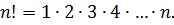
Чтобы не расписывать каждый раз это длинное произведение, просто придумали краткое обозначение. Читается немного непривычно: «эн факториал» (а не наоборот «факториал эн», как может показаться).
Например,
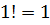
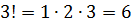
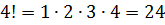
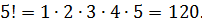
Примеры:
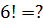
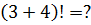
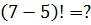
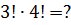
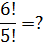
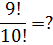
Ответы (в беспорядке): 30; 0,1; 144; 6; 720; 2; 5040.
Свойства факториала
Рассмотрим не очень понятное с точки зрения определения факториала выражение 0! Так уж в математике договорились, что
|
|
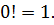
Да-да! Такое вот интересное равенство. Что от единицы, что от нуля факториал один и тот же – единичка. Пока примем это равенство за догму, а вот почему это именно так, будет ясно чуть позже, на примерах.
Следующие два очень похожих свойства:
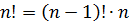
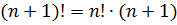
Доказываются они элементарно. Прямо по смыслу факториала.
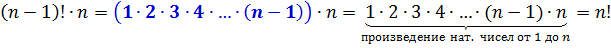
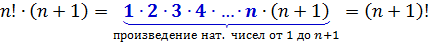
Эти две формулы позволяют, во-первых, легко считать факториал текущего натурального числа через факториал предыдущего числа. Или следующего через текущий.) Такие формулы в математике называются рекуррентными.
Во-вторых, с помощью этих формул можно упрощать и считать некоторые хитрые выражения с факториалами. Типа таких.
Вычислить:
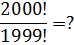
Как действовать будем? Последовательно перемножать все натуральные числа от 1 до 1999 и от 1 до 2000? А вот по свойствам пример решается буквально в одну строчку:
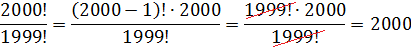
Или так:
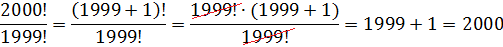
Зачем нужны факториалы и откуда они появились?
Приложений у факториала великое множество. Это и бином Ньютона, и теория вероятностей, и ряды, и формула Тейлора, и даже знаменитое число e, которое представляет собой вот такую интересную бесконечную сумму:
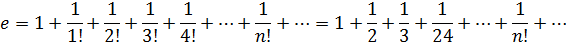
Чем больше задаётся n, тем большее число слагаемых в сумме и тем ближе будет эта сумма к числу e. А в пределе при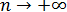 
она станет равна в точности числу e. Но об этом удивительном числе мы поговорим в соответствующей теме. А здесь у нас – факториалы и комбинаторика.
Откуда же они взялись? Они взялись как раз из комбинаторики, с изучения наборов элементов. Простейшим таким набором является перестановка без повторений.