Таблица: A=(a11 a12 …..a1n, a21 a21 a22 ….a2n, ….,am1 am2 …amn) состоящая из m строк и n столбцов, называется матрицей (размера m × n). Если m = n, то матрица называется квадратной. Суммой А + В двух квадратных матриц А = (аij) и В = (bij) порядка n называется матрица С=(сij), всякий элемент которой равен сумме соответственных элементов матриц А и В: сij = аij + bij. Определенное нами сложение матриц будет, очевидно, коммутативным и ассоциативным. Для него существует обратная операция — вычитание, причем разностью матриц A и В служит матрица, составленная из.разностей соответственных элементов заданных матриц. Роль нуля играет при этом нулевая матрица, составленная сплошь из нулей.
Произведением kA, матрицы A = (аij) на число k называется матрица А' = (а'ij),
получающаяся умножением на k всех элементов матрицы A
а'ij = k аij.
При этом выполняются следующие свойства:
k(A + B) = kA + kB;
(k + l)A = kA + lA;
(kl)A = k(lA);
1•A = A.
Пусть A=(a11 a12 …..a1n, a21 a22 ….a2n, ….,am1 am2 …amn), B=(b11 b12 ….b1t, b21 b22 ….b2t,....,bn1 bn2…bnt), C=(c11 c12 …..c1l, c21 c22 ….c2l,....,cm1 cm2 …cml).
Матрица С называется произведением матриц А и В, если сij = ai1 b1j + … + ain bnj, i =1, …, m, j = 1, …,l
Утверждение. Произведение матриц АВ определено тогда и только тогда, когда число столбцов у матрицы А равно числу строк у В.
(∀i ≤ m)(∀j ≤ k)[cij = ai1b1,j + ai2b2j + • • • + ainbnj ].
Для любых матриц A,B,C и чисел (скаляров) Л,М верны тождества:
1. A + B = B + A – коммутативность сложения (матрицы одинаковых размеров);
2. (A + B) + C = A + (B + C) –ассоциативность сложения;
3.. A + θ = A. Здесь θ матрица того же размера,что и А составленная из нулей;
4. A+(−A) = θ здесь-А матрица, элементы которой противоположны элементам матрицы А;
5. λ(A + B) = λA + λB;
6. 6. (λ + µ)A = λA + µA;
7 (λµ)A = λ(µA);
8. 1 · A = A.
1. Если A,B,C –матрицы следующих размеров A = (aij)m, B = (bij)n, C = (cij)k, тогда (A · B) · C = A · (B · C);
2.Если A,B,C-матрицы следующих размеров A = (aij)n/m, B = (bij)k/n, C = (cij)k/n,
Тогда A · (B + C) = A · B + A · C;
3.если A,B,C- матрицы следующих размеров A = (aij)s/k, B = (bij)k/n, C = (cij)k/n,
Тогда (B + C) · A = B · A + C · A.
18.Закон дистрибутивности для матриц. Дистрибутивнось- свойство согласованности двух бинарных операций, определённых на одном и том же множестве.
Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов x,y,z. x*(y+z)=x*y+x*z- дистрибутивность слева. (y+z)*x=y*x+z*x – дистрибутивность справа.
Если операция × является коммутативной, то свойства дистрибутивности слева и справа совпадают.
Аддитивная и мультипликативные операции в кольцах и полях по определению удовлетворяют свойству дистрибутивности.
Если операции сложения и пересечения для односторонних идеалов некоторого кольца (или подмодулей некоторого модуля) удовлетворяют свойству дистрибутивности, то говорят о дистрибутивном кольце (или дистрибутивном модуле).
19. Определитель произведения матриц. Определителем |A | матрицы второго порядка A==(aij),или определителем второго порядка наз-ся число D2-delta2,определяемое формулой:
D2=IAI= Ia11 a12, a21 a22I=a11a22-a12a21.
Произведения а11а22 и а12а21 наз-ся членами определителя.Таким образом определитель второго порядка представляет собой алгебраическую сумму 2! Членов,каждый из которых представляет собой произведение 2-х матричных элементов,взятых по одному из каждой строки и каждого столбца.Один из членов определителя входит в алгебраическую сумму со знаком “+”,а другой со знаком “-”.
При транспонировании матрицы определитель не меняется, то есть:IA стТI=IАI. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть:IABI=IAIIBI.
. Если в матрице A поменять местами две строки, то ее определитель сменит знак. Если матрица имеет две одинаковые строки, то ее определитель равен нулю. Если матрица A имеет две одинаковые строки, то ее определитель равен нулю. Если строку матрицы умножить на число @, то ее определитель умножится на это число. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулюЕсли одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
20. Единичная и обратная матрицы. Если не оговорено противное далее все матрицы квадратные одного порядка из Мn(К).Матрица Е наз-ся единичной, если (\/XeMn(K))[X*E=X=E=X].
Факт:Справедлив общий факт теории колец, в лбом кольце единичный элемент,если существует,то единственен.
Если Е1,Е2 два единичых элемента,то Е1=Е1*Е2=Е2.В кольце Мn(К) единичный элемент существует.Этим свойством,как не трудно вычислить,обладает (1 0 0…0, 010…0, 0 0 1…0,…….0 0 0 …1).
Мтрица В наз-ся обратной матрице А,если А*В=Е=В*А.
Факт: Спаведливо общее утверждение теории ассоиативных колец с единицей, в таком кольце,если элемент имеет обратный,то только один.
Матрица В называется обратной матрицей для квадратной матрицы А, если АВ=ВА=Е. Из определения следует, что обратная матрица В будет квадратной матрицей того же порядка, что и матрица А (иначе одно из произведений АВ или ВА было бы не определено). Обратная матрица для матрицы А обозначается А(-1). Таким образом, если А(-1) существует, то АА(-1)=А(-1)=Е. Из определения обратной матрицы следует, что матрица А является обратной для матрицы А(-1), то есть (А(-1)-1=А. Про матрицы А и А(-1)можно говорить, что они обратны друг другу или взаимно обратны. Если матрица А имеет обратную, то IAI/=0 и IА(-1)I=IАI(-1). Если определитель матрицы равен нулю, то обратная к ней не существует. Если обратная матрица существует, то она единственна.
.
21.Формула обратной матрицы. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле:
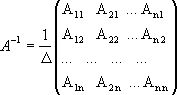 ,где А i j - алгебраические дополнения элементов a i j.
,где А i j - алгебраические дополнения элементов a i j.
Если существуют квадратные матрицы Х и А, удовлетворяющие условию: X × A = A × X = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной матрицей к матрице А и обозначается А-1. Всякая невырожденная матрица имеет обратную матрицу и притом только одну, т. е. для того чтобы квадратная матрица A имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля. Для получения обратной матрицы используют формулу:Xij=(-1)ст(i+j)Mji/detA,, где Мji дополнительный минор элемента аji матрицы А. Cвойства обратных матриц:
1) (А-1)-1 = А;
2) (АВ)-1 = В-1А-1;
3) (АТ)-1 = (А-1)Т;
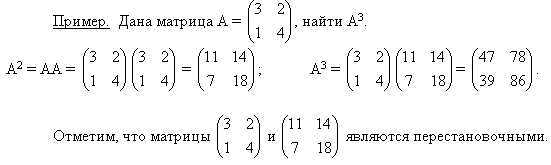
22. Нахождение обратной матрицы элементарными преобразованиями. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: X × A = A × X = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной матрицей к матрице А и обозначается А-1. Всякая невырожденная матрица имеет обратную матрицу и притом только одну, т. е. для того чтобы квадратная матрица A имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля. Для получения обратной матрицы используют формулу:Xij=(-1)ст(i+j)Mji/detA,, где Мji дополнительный минор элемента аji матрицы А. Cвойства обратных матриц:
1) (А-1)-1 = А;
2) (АВ)-1 = В-1А-1;
3) (АТ)-1 = (А-1)Т;
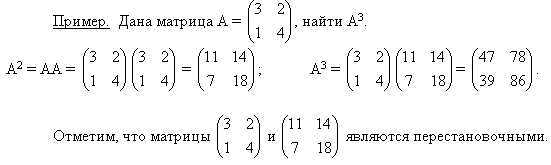
23. Связь операций транспонирования и взятия обратной матрицы с другими операциями над матрицами. Так наз-ся операция над m*n –матрицей А, превращающая ее в m*n матрицу A стT, у которой (i,j)-ый коэфийиент равен (j,i)-ому коэф-ту матрицы А. Операция транспонирования (А->AстТ)-унарная операция в отличии от бинарных операций сложения и вычитания. Св-ва: (AстТ)Т=А -Дважды транспонированная матрица А равна исходной матрице А.Транспонированная сумма матриц равна сумме транспонированных матриц: (A+B)T=AT+BT.Транспонированное произведение матриц равно произведению транспонированных матриц: A+B)T=ВT+АT.При транспонировании можно выносить скаляр:(ЛА)стТ=Ласт Т.Определитель транспонированной матрицы равен определителю исходной матрицы:detA=detAстТ.
С каждой матрицей A = (aij) размера m*n связана матрица B = (bij) размера n*m вида: bij=aij, i=_1,m,; j=_1,n. Такая матрица называется транспонированной матрицей для A и обозначается так Aст T. Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица A = (aij) размера m*n при этом преобразовании станет матрицей размерностью n*m. Операции над матрицами: Умножение матрицы на число. Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен: dij= Лaij. Сложение матриц. Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:cij=aij+bij. Умножение матриц. Умножение матриц (обозначение: AB, реже со знаком умножения AxB) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго: cij=E(от nдо k=1). Комплексное сопряжение. Если элементами матрицы A = (aij) являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна _A=(_aij). Здесь _a— число, комплексно сопряжённое к a.
24. Многочлены от одного неизвестного. Алгоритм деления с остатком. Общий вид уравнения n-ной степени (где n некоторое положительное число) есть: a0xN+a1x(N-1)+…+a(n-1)x+an=0.
- многочленом n-ной степени от неизвестного х.
Многочленом называется лишь выражение вида: a0xN+a1x(N-1)+…+a(n-1)x+an. то есть лишь сумма целых неотрицательных степеней неизвестного x, взятых с некоторыми числовыми коэффициентами. В частности, мы не будем считать многочленами такие выражения, которые содержат неизвестное x с отрицательными или дробными показателями. Для сокращенной записи многочленов употребляются символы f(x), g(x) и так далее. Деление многочленов.
Теория многочленов в определенном отношении похожа на теорию целых чисел, хотя внешне эти две теории не имеют ничего общего. Внутренняя же близость, схожесть этих теорий объясняется тем, что для многочленов, так же как и для целых чисел, можно определить деление и, что еще более важно, деление с остатком.
f(x),g(x)/=0.q(x).Многочлен делится на многочлен, если существует такой многочлен, что выполняется равенство: f(x)=g(x)q(x).
Для многочленов, как и для целых чисел, существует алгоритм деления с остатком.
Теорема о делении с остатком. Для любых двух многочленов f(x) и g(x) можно найти такие многочлены q(x) и r(x, что f(x)=g(x)q(x)+r(x), причем степень r(x) меньше степени g(x) или же r(x)=0. Многочлены q(x) и r(x), удовлетворяющие этому условию, определяются однозначно.
f(x)-r1(x), s(x)=r1(x)-r(x). Если разности f(x)-r(x) и обе делятся наg(x), то их разность также делится наg(x). Если бы многочлен s(x) был ненулевым, то он имел бы степень меньшую, чем g(x), и не мог бы тогда делится наg(x). r1(x)=r(x).Следовательно, s(x)=0, так что.
В практической деятельности для нахождения частного и остатка применяют способ вычисления, называемый «деление углом».
Деление многочлена на многочлен с остатком. Теорема 2.3 Для любого полинома f(x) и любого полинома g(x) = 0 существуют полиномы q(x) и r(x), удовлетворяющие двум условиям:
f(x) = g(x)q(x) + r(x) и deg r(x) < deg g(x)
Полиномы q(x) и r(x) определяются однозначно.
Полиномы q(x) и r(x) называют соответственно частным и остатком от
деления f(x) на g(x). В частности, если здесь положить g = x − λ, то r- константа и мы получаем в
Теорема 2.4 (Безу) Значение полинома f(x) в точке λ равно остатку от деления f(x) на λ: f(λ) = r. На практике деление с остатком выполняют ¾уголком¿, однако част-
ный случай деления многочлена p(x) = a0xn + a1xn−1
+... + an−1x + an на двучлен x−λ удобнее осуществлять по схеме Горнера, даже если нам
нужен только лишь остаток от деления, то есть значение p(λ). Схема получается простым сравнением коэффициентов при одинаковых степенях при раскрытии скобок в правой части тождества a0xN + a1x(N-1) +... + an = (x − λ)(b0x(N−1)+ b1x(N−2) +... + bn−1) + r
25. Наибольший общий делитель многочленов. Алгоритм Евклида. Делители многочлена.Делитель многочлена f(x) - многочлен g(x), такой, что f(x) = g(x)q(x). Наибольший общий делитель двух многочленов. Наибольший общий делитель многочленов f(x) и g(x) - такой их общий делитель d(x), который делится на любой другой их общий делитель.
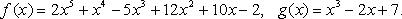
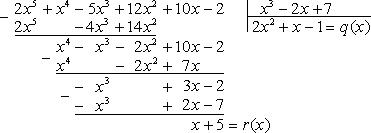
Алгоритм Евклида (алгоритм последовательного деления) нахождения наибольшего общего делителя многочленов f(x) и g(x):
f(x)=g(x)q1(x)+r1(x),
g(x)=r1(x)q2(x)+r2(x),
r1(x)=r2(x)q3(x)+r3(x),
………………………………..
r(k-3)(x)=r(k-2)(x)+r(k-1)(x),
r(k-2)(x)=r(k-1)(x)qk(x)+rk(x),
r(k-1)(x)=rk(x)q(k+1)(x).
Тогда rk(x) - наибольший общий делитель f(x) и g(x).
26. Линейное представление наибольшего общего делителя двух многочленов. Пусть числа а1,а2,…,ак ∈ Z. Тогда существует наибольший общий делитель d этих чисел, при этом d= c1 a1+ c2 a2+ … + ck ak, где сi ∈ Z.Для вычисления наибольшего общего делителя двух целых чисел применяется способ повторного деления с остатком, называемый алгоритмом Евклида. Расширенный алгоритм Евклида помимо наибольшего общего делителя d чисел а и b находит его линейное представление, т. Е. целые числа х и у, для которых выполняется равенство.
27. Схема Горнера. Теорема Безу. Схема Горнера. Теорема Безу.Для деления многочлена n-й степени P(x)=a0xn+a1xn−1+...+an−1x+an на многочлен первой степени x−c обычно используется метод сокращенного деления - схема Горнера. Он получается как следствие определения операции деления многочленов, из которого следует, что при делении многочлена n-й степени на линейный многочлен x−c в остатке может получится либо многочлен нулевой степени (т.е. отличное от нуля число), либо нуль, а степень частного равна n−1. Пусть частное многочленов P(x) и x−c имеет вид: G(x)=α0x(N−1)+α1x(N−2)+...+α(n−2)x+α(n−1), а остаток R(x) равен числу β. Для рассматриваемого случая формула P(x)=Q(x)G(x)+R(x) принимает вид:
a0xN+a1x(N−1)+...+a(n−1)x+an=(x−c)(α0x(N−1)+α1x(N−2)+...+α(n−2)x+αn−1)+β. Раскрывая скобки и приводя подобные члены в правой части равенства, на основании определения равенства многочленов получим систему линейных уравнений дял нахождения коэффициентов α1,α2,...,α(n−2),α(n−1), β: α0=a0, α1=a1+ca0, α2=a2+ca1,..., α(n−1)=a(n−1)+ca(n−2), β=an+ca(n−1).
Первое уравнение системы дает значение α0=a0. Подставляя это значение α0 во второе уравнение системы, получаем α1=a1+ca0. Подставляя полученное значение α1 в третье уравнение системы, получаем значение α2 и т.д. Последним будет найдено выражение для остатка β:
Теорема Безу. Остаток от деления многочлена F(x) на линейный двучлен x–a равен значению многочлена в точке а, т. е. числу F(a). Доказательство: Разделим F(x) на x–a с остатком, т. е. представим его в виде F(x)=(x-a)Q(x)+R. Как было сказано выше, остаток R является константой. Подставим x=a: F(a)=(a-a)Q(a)+R => R=F(a), что и требовалось доказать.
28.Кратные корни многочлена. Определение. Число называется корнем полинома f, если f(a=0).В силу теоремы Безу это равносильно тому, что: f: (x-a). Определение. Число @ называется корнем кратности k полинома, если f: (x-a)N и f: (x-a)(K+1), keN. Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями. Теорема. Если @ — корень кратности k полинома f, то @— корень кратности k-1 полинома f’. Если @ — общий корень f,f’, то @— кратный корень f.
.