Расчетно-графическая работа № 6 «Расчет вала на прочность при совместном действии кручения и изгиба»

 

Проверить прочность вала, испытывающего совместное действие кручения и изгиба, на статическую прочность при кратковременных пере­грузках в целях предотвращения пластических деформаций. Схему вала, схему сил в зацеплении косозубого зубчатого колеса (F_t F_r, F_a), нагрузку на вал со стороны ременной передачи F_e, значения необходимых для рас­чета параметров берем из таблиц 9.1, 9.2, 9.3 и 9.4.

Силы в зацеплении зубчатого колеса рассчитываются по зависимостям: -радиальная, - осевая, где - угол зацепления, угол наклона зуба.

Крутящий момент T, передаваемый валом, определяется по формуле

 

(9.4)

 

где d₁ - делительный диаметр зубчатого колеса, м.

Допускаемые напряжения , где - предел текучести материала вала.

 

 

Таблица 9.1 - Схемы валов для расчетно-графической работы №6

 

 

 

 

Таблица 9.3 - Нагрузка на вал со стороны ременной передачи для расчетно-графической работы №6

 

 

 

Таблица 9.4 - Значения параметров для расчетно-графической рабо­ты №6

 

Но­мер вари­анта	Окружная сила Ft,кН	На­грузка навал Fb,kH	Делит, диам. зуб. кол. d1MM	Диа­метр вала d, мм	а, мм	мм	с, мм	Коэф. пере­грузки, кп	Предел теку­чести , МПа
		0,5						1,4
		0,6						2,5
		0,7						1,6
		0,8						1,8
		0,9
								2,2
		1,1						2,4
		1,2						2,6
		1,3						2,8
		1,4

 

 

Решение

 

1. Составляем расчетную схему вала (рис. 9.1, б).b

2. Строим эпюру крутящего момента Т (рис. 9.1, в).

На всей длине вала СД действует крутящий момент Т= 2800 .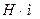

3. Исходя из принципа независимости действия сил, рассматриваем схему вала в двух плоскостях: в вертикальной плоскости XOY (рис. 9.1, г) и в горизонтальной плоскости XOZ (рис. 9.1, е).

 

4. Определяем реакции R_Ay и R_By в опорах А и В, действующие в вер­тикальной плоскости (рис. 9.1, г). Принято силы F_r и F_a рассматривать в одной плоскости.

 

 

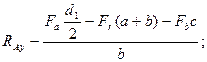
Отрицательный знак реакции R_Ay означает, что она направлена в

противоположную сторону. Поэтому на расчетной схеме исправляем ее направление.

Выполним проверку:

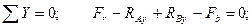
Равенство выполняется, реакции найдены верно.

5. Определяем реакции R_Az и R_Bz в опорах А и В, действующие в го­ризонтальной плоскости (рис. 9.1,е):

Выполним проверку:

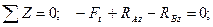
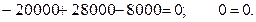
Равенство выполняется, реакции найдены верно.

 

 

 

Рисунок 9.1 - Построение эпюр к РГР №6

 

 

6.Строим эпюру изгибающих моментов в вертикальной плоскости (рис. 9,1, д). Балку делим на три участка СА, АВ и ВД. Для этих участков берем сечения х₁ х₂, х₃ и составляем уравнения изгибающих моментов, по которым строим эпюру.

Участок СА

 

при

 

при

 

Участок АВ

 

при х₂ = а;

 

при х₂ = а + b;

 

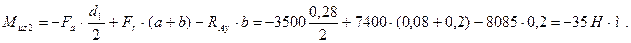
Участок ВД

 

при

 

при х₃ = с;

 

7. Строим эпюру изгибающих моментов в горизонтальной плоскости (рис. 9.1, ж).

Участок СА

 

при х₁ = 0;

 

при х₁ = а;

 

Участок АВ

 

при х₂ = а;

 

при х₂ = а + b;

Участок ВД

8. Строим суммарную эпюру изгибающих моментов (рис. 9.1, з). Для этого определяем значения суммарного изгибающего момента в точках А, В, С и Д по зависимости

точка С,

точка А,

точка В,

точка Д,

Причем если на одной из эпюр в какой-либо точке был скачок, то в этой точке нужно считать дважды по двум точкам в месте скачка та­ким образом, чтобы на эпюре также получился скачок.

9. Из анализа эпюр (рис. 9.1, в, з) видно, что наиболее опасным явля­ется сечение в точке А. В этой точке действует максимальный суммарный изгибающий момент 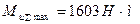и крутящий момент Т = 2800 Н • м. Сечение вала в точке А находится в сложном напряженном состоянии. Эквивалентное напряжение в этом сечении определяем по четвертой теории прочности

где 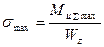- максимальное нормальное напряжение, возникающее

от изгиба вала;

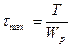- максимальное касательное напряжение, возникающее от кручения;

W_z - осевой момент сопротивления сечения вала, который для кругло­го вала равен

 

W_z = 0,1 d ³ = 0,1 • 50³ = 12500 мм³;

W_p - полярный момент сопротивления сечения вала, который для круглого вала равен:

W_z = 0,2 d ³ = 0,2 • 50³ = 25000 мм³;

 

 

 

Эквивалентное напряжение с учетом перегрузок

Для статической прочности вала при кратковременной перегрузке должно выполняться условие

где

Таким образом, условие статической прочности вала при кратковре­менной перегрузке выполняется.

 

9.3 Контрольные вопросы

 

1. Какое напряженное состояние называется сложным?

2. Как определяется условие прочности при сложном напряженном состоянии?

3. Запишите третью теорию прочности.

4. Запишите четвертую теорию прочности.

 

Список литературы

1. Яблонский И.И. Курс теоретической механики / И.И. Яблонский, В.Н. Никифоров. - СПб.: Лань,1999. - 768 с.

2. Теория механизмов и машин / К.В. Фролов, С.А. Попов, А.К. Му­сатов и др.; Под ред. К.В. Фролова. - М.: Высш. шк., 1987. - 496 с.

3. Прикладная механика / А.Т. Скойбеда, А.А. Миклашевич, Е.Н. Левковский и др.; Под ред. А.Т. Скойбеда. - Минск: Вышэйшая школа, 1997.-522 с.

4. Биргер И.А. Расчет на прочность деталей машин / И.А. Биргер, Б.Ф. Шорр, Г.Б. Иосилевич. - М.: Машиностроение, 1979.

 

ПРИКЛАДНАЯ МЕХАНИКА

 

Составители: Бережной Сергей Борисович

Сутокский Виталий Геннадьевич

Остапенко Олег Иванович

 

Редактор А.В. Снагощенко, Л.В. Троицкая, Т.П. Горшкова

 

 

Компьютерная верстка Ю.С. Трубникова

 

Подписано в печать Формат 60x84 /16

Бумага оберточная № 1 Офсетная печать

Печ.л. 4,0 Тираж 200 экз.

У сл-печ. л. 3,75 Изд. № 97

Уч-изд.л. 2,85 Заказ №203

Цена 18 руб.

 

 

Лиц. ИД№ 02586от 18.08.2000

Кубанский государственный технологический университет

350072, Краснодар, ул. Московская, 2-а

Лиц. ПД№ 10-47020 от 11.09.2000

Типография КубГТУ. 350058, Краснодар, ул. Старокубанская, 88/4.