91
в эксперименте, являются диагностичными. Среди них есть слишком легкие и слишком трудные, по существу не позволяющие дифференцировать детей по степени овладения моделирующими перцептивными действиями. Процент успешного решения таких задач выходит за пределы нормы (не менее 15% и не более 80%), принятой в психологической диагностике для отбора задач, включаемых в целостные батареи (М. С. Бернштейн, 1968).
Таблица 13
Количество правильных решений каждой задачи детьми разных
возрастных групп детского сада с первой попытки (в % к общему
числу решений по каждой группе)
| Группа испытуемых | Номер задачи | ||||||
| Вторая младшая | |||||||
| Средняя | |||||||
| Старшая | |||||||
| Подготовительная к школе |
Оказалось, что для детей младших групп пригодными являются задачи, требующие одновременного учета не более одного-двух признаков сложной формы; для детей подготовительных к школе групп, напротив, — только требующие сложного системного перцептивного действия, выявляющего все намеченные заданиями признаки формы или наиболее сложные их комбинации, включающие ракурс и соотношение элементов; для детей средних и старших групп — задачи разной сложности (в том числе и максимальной), включающие ориентировку на комбинацию из двух и более признаков.
Хотя проверенный в эксперименте 1-й вариант заданий оказался принципиально пригодным для выявления степени овладения моделирующими перцептивными действиями у детей средней и старшей возрастных групп, он еще нуждался в дальнейшем усовершенствовании и специальном приспособлении для диагностических целей. Часть задач требовала усложнения, а весь набор в целом — проверки на надежность получаемых с его помощью данных, дискриминабельность и удобство использования.
92
Поэтому при его переработке мы ввели, наряду с уже опробованными задачами, новые, на наш взгляд более сложные, и каждую представили в двух равно-трудных и идентичных по требуемым операциям вариантах (для проверки надежности методики путем расчета коэффициента корреляции между результатами, полученными по двум равноценным наборам задач).
Предварительная проверка дала нам также основание отказаться от повторных предъявлений задач, поскольку они слишком удлиняли процедуру обследования и по существу не давали действительной характеристики уже сложившегося у ребенка моделирующего перцептивного действия. В связи с этим в новом, 2-м варианте заданий была предусмотрена оценка результатов только на основании решений «с места», а также учтена возможность сокращения процедуры обследования.
2-й вариант. Новый вариант методики включал 16 задач (по две аналогичных). Поскольку при проверке была подмечена обучаемость некоторых детей способам решения задач нарастающей трудности, в этом варианте мы предъявляли задания в обратном порядке. Это несколько изменило и процедуру обследования, позволив отказаться от предъявления детям простых задач, если они безошибочно справлялись с двумя предыдущими, более сложными. Первая и вторая задачи требовали от ребенка осуществления 8 преобразований (по 2 преобразования каждого из указанных выше типов); третья и четвертая — по 4 преобразования; пятая — восьмая — по 2 (либо на изменение формы и положения элементов, либо на изменение их ракурса и соотношения), и, наконец, последние 8 задач требовали по одному преобразованию того или иного типа.
В 2 первых задачах для построения фигур использовалось по 4 геометрических вкладки, в остальных задачах — по 2 вкладки (рис. 3). Соответственно числу заданных преобразований начислялась количественная оценка по каждому заданию. За каждое правильно выполненное преобразование давалось 1 очко. Максимальная оценка в этой методике составляла 40 баллов.
Этот вариант заданий прошел экспериментальную проверку на 55 детях средней и 42 детях старшей группы детского сада Москвы. В результате статистической обработки собранного материала были получены следующие
93
характеристики методики: для средней группы M=26,5; σ=7,6; R=0,88; для старшей группы M=28,1; σ=8,6; R=0,90.

Рис. 3.
Поскольку экспериментальная проверка методики дала удовлетворительные результаты, мы предприняли ее массовую проверку на 390 детях, посещавших детские сады Москвы, Риги и Тулы. Методика была опробована на 192 детях из средних и на 198 детях из старших групп. В результате этой проверки были получены следующие данные: для детей средних групп M=22,2; σ=9,1; R=0,86; для детей старших групп M=30,4; σ=8,0; R=0,85. Была рассчитана также достоверность различия средних показателей для средних и старших возрастных групп. Это различие оказалось значимым на уровне p≤0,001.
94
Все эти данные свидетельствовали о достаточной статистической обоснованности методики. Однако при попытке перевода «сырых» баллов в используемую нами стандартную шкалу Векслера с M=10 и σ=3 мы обнаружили, что максимальное количество «сырых» баллов (40) соответствует у детей средних групп только 16, а у детей старших групп — 15 стандартным очкам (при 19 возможных). Это означало, что методика не улавливает весь диапазон возможных различий между детьми, причем особенно слабо она дифференцирует наиболее продвинутых детей и, следовательно, не все задачи, входящие в нее, обладают достаточной степенью трудности. Кроме того, в ходе массовой проверки было замечено, что, хотя дети довольно легко входят в работу и не воспринимают задания как обременительные и скучные, процедура обследования каждого ребенка является слишком длительной (15—20 мин) и следует подумать о ее сокращении.
Таким образом, перед нами возникла задача, сохранив положительные стороны методики, устранить имеющиеся в ней недостатки (недостаточную дискриминабельность и излишнюю длительность процедуры обследования).
3-й вариант. Задачи последнего варианта принципиально не отличались от предыдущих, но превосходили их по степени трудности. Для решения каждой из них требовался учет всех вышеперечисленных признаков сложной формы, а следовательно, функционирование сложного системного перцептивного действия, улавливающего разнообразные связи и зависимости между ними. Разница между отдельными заданиями состояла лишь в степени сложности комбинаций признаков, которые требовали учета в каждом случае (рис. 4). Для сокращения времени обследования число задач было сокращено до 10.
Каждая фигура в задачах (как требовавшая преобразования, так и образец) собиралась из доски-основания и 4—5 геометрических вставок. В процессе перестройки фигуры дети должны были осуществлять либо по 8 преобразований (задачи 1—4), либо по 4 (задачи 5—10). Чтобы определить характер преобразований, требуемых в 4 первых задачах (наиболее трудных), необходимо было вычленить форму, ракурс, положение и соотношение
95
элементов на обеих сторонах фигуры (нижней и верхней) и привести их в соответствие с образцом. В остальных задачах количество признаков, по которым «рабочая» фигура отличалась от образца, было сокращено в 2 раза. Преобразования шли только по 2 параметрам, различным для верхней и нижней частей фигуры.
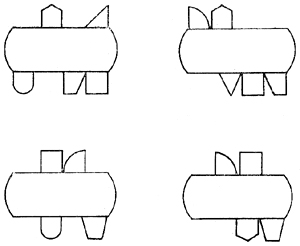
Рис. 4.
Набор задач, использованный в этом варианте, был с незначительными исправлениями принят в дальнейшем как окончательный.
В экспериментальной проверке этого варианта методики (он идет под номером 2а) приняли участие дети средних и старших возрастных групп детского сада Москвы, по 40 человек каждого возраста.
Экспериментальная проверка показала, что 3-й вариант задач по успешности решения стоит ближе к допустимой норме, чем предыдущие (63% — для средней группы и 69% — для старшей). Дифференцирующая сила заданий заметно повысилась. Внутри каждой возрастной группы распределение «сырых» и стандартных очков значительно расширилось. Оно стало захватывать большую часть шкалы. Соотношение средних показателей для группы и стандартных отклонений стало несколько лучшим (для средней группы M=31,65; σ=17,2; для старшей — M=40,40; σ=10,6). Расчет достоверности различия средних для детей обеих возрастных групп показал, что оно является значимым на уровне вероятности p≤0,01. Коэффициент надежности методики для обеих возрастных групп оказался вполне удовлетворительным
96
(для средней группы R=0,97; для старшей — R=0,87).
В эксперименте были проверены также два разных варианта оценки результатов решения отобранных задач. В первом варианте за каждое правильно выполненное преобразование начислялся 1 балл. Ошибки, не предусмотренные заданием, не учитывались в количественной оценке. Они входили только в качественную характеристику системы операций, которой владеет ребенок. Максимальное количество очков, которое мог набрать ребенок по всем задачам, равнялось 56. Во втором варианте максимальный для каждой задачи балл (соответствующий количеству заданных в ней преобразований) начислялся только за точное воспроизведение образца, т. е. при условии, что ребенок, осуществляя заданные преобразования, не допускал никаких других отклонений от образца. Расчет коэффициента корреляции между результатами одних и тех же детей, выраженными в оценках того и другого типа, оказался достаточно высоким (r=0,91), что позволяло пользоваться любой из этих оценок.
Мы остановились на первом варианте, поскольку он дает возможность довольно быстро и однозначно устанавливать типы преобразований (из заданных), наиболее трудные для того или иного ребенка, и, следовательно, обнаруживать отклонения в системе операций, входящих в структуру перцептивного действия.
Кроме того, мы провели качественный анализ методики, использовав для этой цели данные тех же 80 детей. Качественные особенности решения детьми всего набора задач позволили разделить испытуемых на 4 группы, различающиеся по степени овладения моделирующим перцептивным действием.
Первая группа состояла из детей, не обнаруживших адекватной ориентировки на признаки сложной формы при любом их сочетании. Правильные решения у них появлялись случайно.
Во вторую группу вошли дети, показавшие отсутствие ориентировки на все признаки сложной формы в случаях, когда был необходим их одновременный учет, и наличие ориентировки на эти же признаки в случаях их попарного анализа.
Третью группу составили дети, оказавшиеся не в состоянии учесть весь комплекс признаков сложной
97
формы в тех задачах, где эти признаки были представлены одновременно. Эти задачи решались частично, с ошибками на положение или ракурс элементов, т. е. на наиболее трудно выделяемые признаки. В более простых задачах дети, отнесенные к этой группе, допускали случайные ошибки.
В четвертую группу вошли дети, успешно ориентирующиеся на все признаки сложной формы в любом их сочетании и допускающие лишь отдельные случайные ошибки и неточности.
Сравнение средних результатов, полученных детьми соседних групп, дало значимые различия во всех случаях на уровне вероятности p≤0,001; 0,01 и 0,05. Эти данные приведены в табл. 14.
Таблица 14
Распределение детей среднего и старшего возраста по группам на
основе количественной и качественной оценки результатов
(методика 2а)
| Качественная группа | Количество детей | M | σ | Значимость различий средних показателей для смежных групп |
| I | 16,9 | 11,20 | p≤0,001 p≤0,05 p≤0,01 | |
| II | 36,5 | 7,84 | ||
| III | 46,0 | 3,78 | ||
| IV | 53,4 | 1,90 |
3-й вариант методики прошел массовую проверку в средних и старших группах детских садов Москвы, Московской области и Краснодарского края. В его проверке приняло участие свыше 500 детей. В ходе проводимых проверок методика подверглась некоторым уточнениям и усовершенствованиям. Диагностический материал (деревянные доски с пазами и вставками) был заменен на более легкий, портативный и удобный для быстрого употребления (детали из цветного пластика без пазов и «ножек»).
Действие вкладывания геометрических фигурок-вставок в пазы было заменено простым прикладыванием элементов к верхней и нижней граням основания. Образцы стали даваться в форме изображений
98
такого же размера, что и воссоздаваемая фигура (см. рис. 5).

Рис. 5.
3-й вариант заданий рассматривается нами как пригодный для диагностики1. Его окончательная проверка и стандартизация были проведены в 6 детских садах Москвы на 100 детях средней и 100 детях старшей возрастных групп.
Результаты проверки показали, что для детей средней группы M=25,5; σ=14,9; R=0,98; для детей старшей группы M=39,3; σ=10,7; R=0,94.
Следующий этап нашей работы состоял в создании методики, направленной на выявление степени овладения моделирующими перцептивными действиями у детейподготовительной к школе группы. Как уже говорилось, методика, описанная нами выше, оказалась для таких детей слишком легкой и, следовательно, недостаточно дискриминабельной. Необходимо было найти новый, более сложный вид заданий. Кроме того, мы стремились придать этим заданиям новую форму, позволяющую проводить групповое обследование детей в условиях, приближающихся к условиям учебной работы
99
в группе. Поэтому мы не могли пойти по линии усложнения заданий на перестройку фигуры по образцу, включенных в конструктивную деятельность и требующих манипулирования реальными объектами.
В поисках заданий, требующих выполнения перцептивного действия интересующего нас типа и вместе с тем отвечающих необходимым условиям обследования детей подготовительной группы, мы остановились на заданиях, предусматривающих зрительное «конструирование» фигуры определенной формы из заданных элементов. Принцип построения подобных заданий был заимствован нами из экспериментальных исследований А. Р. Лурия (1948) и В. П. Сохиной (1962). В исследовании А. Р. Лурия было показано огромное значение для развития восприятия дошкольников строительных игр, в процессе которых дети создавали конструкции по заклеенным (т. е. контурным) образцам, самостоятельно подбирая и комбинируя нужные элементы. Работа В. П. Сохиной была специально посвящена анализу перцептивных действий, складывающихся при выполнении подобных заданий и обеспечивающих его успешность.
Эти действия были определены автором как перцептивные действия моделирующего типа.
Конкретные задачи, предлагавшиеся детям в работе В. П. Сохиной, состояли в отборе нужного количества плоскостных элементов разной формы (из числа заданных) для заполнения контурного изображения здания. Дети, у которых было сформировано моделирующее перцептивное действие, оказывались в состоянии произвести такой отбор чисто зрительным путем, до начала реального заполнения контура.
1-й вариант. Задание, разработанное нами, отличалось от задания В. П. Сохиной тем, что оно не включало возможности реального оперирования элементами при заполнении контура: и то и другое было представлено в виде изображений на одной плоскости листа. Кроме того, мы решили при составлении отдельных задач варьировать не форму заполняемого контура (при сохранении одних и тех же элементов), как это было у В. П. Сохиной, а форму и число заданных элементов при сохранении одного и того же контура. Это позволило добиться более четкой характеристики входящих в
100
моделирующее перцептивное действие отдельных операций, которыми владеет ребенок.
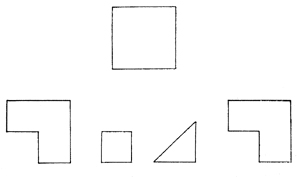
Рис. 6.
В нашем задании ребенку предлагался сброшюрованный набор рисунков; каждый рисунок содержал контурное изображение геометрической фигуры (круга или квадрата), а под ним — изображение нескольких (от 2 до 4) фигурок разной формы, сочетание которых в определенном положении давало возможность заполнить контур, а также еще нескольких лишних фигурок. Ребенок должен был на каждом листе отметить карандашом те фигурки, из которых можно сложить круг (или квадрат) (см. рис. 6).
В первых четырех задачах нужно было выбрать две фигурки из четырех, в следующих четырех задачах — три из шести, в последних четырех — четыре из восьми.
Фигуры на рисунках по своей форме, положению и ракурсу были заданы таким образом, что для их отбора и соотнесения друг с другом при визуальном заполнении контура необходимо было выполнить ряд операций: выделить и оценить форму отбираемых элементов, придать им соответствующий ракурс и положение относительно друг друга, определить общие размеры собранной из них фигуры и соответствие последней заданному контуру. При этом требовалось удержать в представлении уже выполненную операцию и учитывать ее в ходе дальнейшего сопоставления отбираемых частей. Вместе с увеличением числа элементов, которыми оперирует ребенок в задачах, усложняется и вся система перцептивных операций, необходимых для правильной ориентировки
101
в условиях задания. По результатам их выполнения можно судить о качественных и структурных особенностях сложившегося у ребенка моделирующего перцептивного действия.
При количественной оценке успешности выполнение задания ребенок получал 1 балл за каждый правильно отмеченный элемент, а за каждый элемент, отмеченный неверно, 1 балл снимался. Если количество ошибочно отмеченных элементов превышало количество отмеченных верно, решение задачи оценивалось как нулевое.
Первый вариант методики был проверен в лабораторном эксперименте на 43 детях подготовительных групп яслей — детского сада Москвы и получил следующие статистические характеристики: M=19,2 (при максимальной оценке 36 баллов); σ=4,3; R=0,71.
Эти характеристики позволили перейти к массовой проверке методики, которая была осуществлена на 584 детях детских садов Москвы и Саратовской области. Результаты обработки данных массовой проверки оказались следующими: M=18,3; σ=4,9; R=0,57.
Значительное снижение надежности результатов при массовом применении методики, длительность процедуры обследования детей и трудности осуществления качественного анализа результатов потребовали внесения в методику существенных изменений. Основное внимание было направлено на снижение числа случайных решений и, следовательно, на повышение надежности методики.
2-й вариант. Поиск путей увеличения надежности методики заставил нас прибегнуть к широко распространенному приему — увеличению числа предъявляемых детям задач. Кроме того, предполагалось, что сокращение числа элементов, из которых производился выбор частей фигуры, и специальное обозначение одного из них сделает задачу более понятной детям и устранит случайные решения, связанные с недостаточным пониманием инструкции. В результате предварительной экспериментальной проверки влияния каждого из указанных моментов на надежность (устойчивость) результатов решения задач был создан промежуточный вариант методики, в котором количество задач, включенных в методику, было увеличено до 16. Фигуры, которыми оперировал ребенок, частично были изменены. В каждой
102
задаче был выделен основной элемент, необходимый для воссоздания фигуры-образца. Этот элемент располагался в центре листа под образцом и отмечался крестиком. Остальные элементы располагались слева и справа от основного (рис. 7).
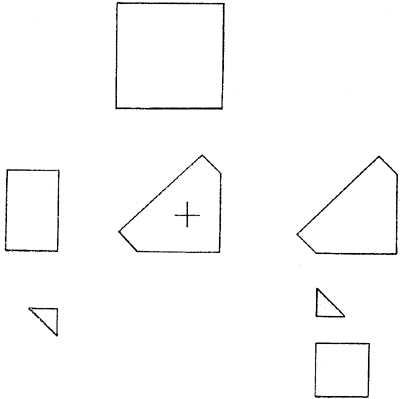
Рис. 7.
Максимальное число фигур, из которых производился необходимый выбор, было сокращено до 5. Максимальная оценка, которую мог получить ребенок, составляла 28 баллов.
Этот вариант методики был опробован в эксперименте на 39 детях подготовительных групп яслей — детского сада № 515 Москвы. Статистические показатели методики оказались следующими: M=18,6; σ=6,7; R=0,67.
Коэффициент надежности повысился, но при попытке перевода исходных данных в стандартную шкалу обнаружилась явно недостаточная дискриминабельность Методики: слишком большое количество, с одной стороны, нулевых, а с другой — полных решений всей системы задач.
103
Это свидетельствовало о том, что методика, измененная одновременно по трем параметрам (выделение одного элемента в качестве основного, размещение остальных вокруг него и сокращение их количества), становилась слишком легкой для наиболее продвинутых детей. Вместе с тем она по-прежнему оставалась довольно трудной для тех, кто плохо понимал инструкцию на примере решения вводных задач.
3-й вариант. При разработке следующего варианта методики мы попытались учесть эти моменты. Выделение одного из нужных элементов было сохранено (в отличие от остальных этот элемент был заштрихован), но размещение элементов и их количество было таким, как в 1-м варианте. Одновременно были предприняты шаги для придания инструкции более конкретной формы: перед решением задач каждого типа (т. е. предполагавших составление сочетания из 2, 3, 4 элементов) ребенку сообщалось, из какого количества частей он должен «сложить» фигуру.
Изменения были внесены и в систему оценки успешности выполнения заданий. За полностью правильное решение каждой задачи ребенок получал столько баллов, сколько требовалось элементов для составления фигуры. При наличии каких бы то ни было ошибок (выборе лишних элементов или неполном выборе нужных) решение задачи оценивалось как нулевое.
Этот вариант методики был проверен в лабораторных условиях на 30 детях подготовительных к школе групп и дал значительное повышение надежности до R=0,88.
Проверка методики в условиях группового обследования 72 детей базовых детских садов Москвы дала следующие результаты: M=18,2 (при максимальном балле 36); σ=4,9; R=0,78.
Дальнейшее опробование методики на 259 детях из детских садов Москвы и Московской области привело к менее удовлетворительным результатам M=15,6; σ=7,4; R=0,65.
При этом вновь оказалась сниженной дискриминабельность методики как в нижней, так и в верхней части шкалы.
4-й вариант. В последнем варианте методики мы добивались увеличения дискриминабельности и одновременно искали возможность сокращения времени обследования
104
за счет внесения изменений в характер вводных задач и в форму подачи инструкции.
Выделение элементов штриховкой было снято. Количество элементов, из которых производился выбор, было уравнено во всех задачах (2, 3 и 4 элемента равным образом выбирались из 6). Количество вводных задач было увеличено до 3, причем в одной из них ребенку демонстрировалось составление фигуры из 2, в другой — из 3 и в третьей — из 4 элементов. Инструкция давалась на примере решения вводных задач, тем самым необходимость дополнительных указаний о количестве элементов, которое следует отметить, устранялась. (См. Приложение, методика 3).
Указанный вариант методики прошел несколько экспериментальных проверок, в ходе которых уточнялись типы вводных заданий, формы предъявления инструкции, осуществлялся поиск достаточно удобной в использовании и вместе с тем валидной количественной оценки, выделялись возможности сокращения времени обследования.
В ходе отработки данная методика была опробована на 570 детях из детских садов Москвы и Московской области. Ее окончательная стандартизация была осуществлена на 102 детях подготовительных к школе групп 5 детских садов Москвы. Были получены следующие показатели: M=16,1 (при максимальной оценке 36 баллов); σ=7,8; R=0,75, значимый на уровне p≤0,001.
При переводе данных в стандартную шкалу обнаружилась достаточная дискриминабельность методики.
Систематический анализ результатов применения данной методики в практике психологического обследования детей показал, что степень развития у ребенка моделирующих перцептивных действий объективно обнаруживается в успешности решения задач определенной сложности, точности отбора элементов, необходимых для воспроизведения образца, учета их взаимного соответствия друг другу, а также в числе и характере допущенных ошибок. Дети (102 ребенка), обследованные в процессе окончательной стандартизации методики, были распределены на 4 группы.
К первой группе были отнесены дети, которые в условиях нашей методики обнаружили полную неспособность
105
к выполнению моделирующих перцептивных действий. У них встречаются лишь отдельные правильные решения, не зависящие от сложности предъявляемых задач. Такие решения могут быть квалифицированы только как случайные. При решении большинства задач дети этой группы создают комбинации элементов, абсолютно не соответствующие форме заданной фигуры.
У детей, отнесенных нами ко второй группе, действие перцептивного моделирования ограничено системой операций, позволяющей учитывать форму, положение и пространственное соотношение не более двух элементов целой фигуры. Соответственно этому дети данной группы правильно решают почти исключительно те задачи, которые требуют сочетания двух элементов. В остальных случаях они либо подменяют задачу, подбирая элементы, по своей общей форме сходные с заданной фигурой, либо составляют неадекватные сочетания.
В третью группу вошли дети, в достаточной мере владеющие всей системой операций, необходимых для выполнения моделирующего перцептивного действия в условиях наших заданий. Вместе с тем это действие обладает еще недостаточной точностью и гибкостью. Дети либо достигают правильного результата в любых задачах, либо допускают неточные решения, при которых выбранная ими совокупность элементов дает возможность составить фигуру, сходную с заданной, но не идентичную ей. Встречающиеся у детей этой группы отдельные грубые ошибки носят случайный характер.
К четвертой группе были отнесены дети, которые в условиях нашей методики обнаружили высокую степень овладения моделирующим перцептивным действием. Они допускали лишь отдельные неточности решений, не зависящие от степени сложности задачи.
Результаты сопоставления качественных и количественных данных, полученных в результате применения данной методики для обследования вышеназванных детей, приведены в табл. 15.
Эти данные позволяют считать использованную в методике количественную оценку достаточно отражающей качество осуществляемой детьми ориентировки, а методику — пригодной для диагностирования разной степени овладения указанными моделирующими перцептивными действиями.
106
Таблица 15
Распределение детей от 6 до 7 лет по группам на основе
количественной и качественной оценок результатов выполнения
заданий (методика 3)
| Качественная группа | Количество детей | M | σ | Значимость различий средних показателей для смежных групп |
| I | 30,1 | 1,73 | p≤0,001 p≤0,001 p≤0,001 | |
| II | 21,0 | 3,45 | ||
| III | 12,8 | 3,52 | ||
| IV | 4,4 | 1,86 |
Нашей дальнейшей задачей являлась разработка методики для детей младшей группы. Приступая к ее разрешению, мы вновь обратились к заданию на перестройку фигуры по образцу, использованному нами для средних и старших дошкольников. Однако здесь мы столкнулись с существенными трудностями. Как уже говорилось выше, предъявление первого варианта этой методики воспитанникам младшей группы показало ее явную трудность для таких детей. Но дело заключалось не только в том, что дети, как правило, не могли правильно решить предложенные им задачи. Они часто вовсе не принимали этих задач, либо утверждая, что предложенная для перестройки фигура «такая же», как образец, либо вытаскивая из основания все элементы и принимаясь строить объект заново.
В работе С. Каур (1970) при изучении формирования моделирующих перцептивных действий у детей младшей группы было установлено, что принятию и выполнению заданий на перестройку фигуры по образцу (которое достигалось только в результате специального обучения) предшествует принятие более простых заданий на построениефигуры по образцу из заданных элементов. Кроме того, С. Каур был использован прием «опредмечивания» образцов: называния их машинами, паровозиками и т. п., что облегчало вовлечение детей в работу.
Используя эти данные, мы разработали вариант нашей методики, рассчитанный на младших
107
дошкольников1. Фигуры-образцы с самого начала строились как модели разных предметов (самолета, танка, коляски и др.). Фигурки-детали не вставлялись в пазы основания, а просто прикладывались к нему, что облегчало «техническую» сторону выполнения задания. Фигуру-основу мы оставили такой же формы, как и раньше: это был прямоугольник с закругленными боковыми сторонами. Детали, с помощью которых строились фигуры сложной формы, были следующими: квадраты — маленький и большой, круги — два маленьких и один большой, полукруг, сектор, фигура такой же формы, как основа, только меньшего размера и узкий длинный прямоугольник. Этот набор позволил создать фигуры, при воспроизведении которых от испытуемого требовалось учитывать 4 параметра: форму, величину, ракурс и положение каждого элемента.