Кольцо многочленов от одной переменной.
Деление многочлена на двучлен. Схема Горнера.
Пусть 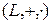 - коммутативное кольцо с единицей, K подкольцо этого кольца, содержащее единицу, и
- коммутативное кольцо с единицей, K подкольцо этого кольца, содержащее единицу, и 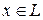 .
.
Обозначим через K [ x ] пересечение всех подколец кольца 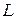 , содержащих элементы кольца K и элемент x. K [ x ] - кольцо относительно операции в кольце
, содержащих элементы кольца K и элемент x. K [ x ] - кольцо относительно операции в кольце 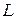 .
.
Определение. Кольцо K [ x ] называется простым расширением кольца K посредством присоединения элемента x.
Элемент 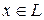 называется алгебраическим элементом над K, если существуют
называется алгебраическим элементом над K, если существуют 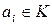 не все равные нулю, что
не все равные нулю, что
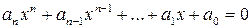 .
.
Элемент 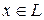 , не являющийся алгебраическим над кольцом
, не являющийся алгебраическим над кольцом 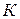 , называется трансцендентным элементом над кольцом K.
, называется трансцендентным элементом над кольцом K.
Кольцо K [ x ] называется простым алгебраическим расширением кольца K, если x – алгебраический элемент над K. Если же 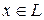 трансцендентный элемент над K, то кольцо K [ x ] называется простым трансцендентным расширением кольца K.
трансцендентный элемент над K, то кольцо K [ x ] называется простым трансцендентным расширением кольца K.
Пример. 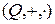 - кольцо рациональных чисел,
- кольцо рациональных чисел, 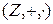 - кольцо целых чисел.
- кольцо целых чисел.  является алгебраическим над кольцом Z, т.к.
является алгебраическим над кольцом Z, т.к. 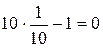 .
. 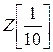 - простое алгебраическое расширение кольца Z состоит из рациональных чисел, представленных в виде конечной десятичной дроби.
- простое алгебраическое расширение кольца Z состоит из рациональных чисел, представленных в виде конечной десятичной дроби.
Определение. Простое трансцендентное расширение K [ x ] коммутативного кольца K с единицей посредством присоединения к кольцу K трансцендентного над кольцом K элемента x называется кольцом многочленов
от переменной x.
Элементы кольца K [ x ] называются многочленами и обозначаются f (x), g(x),
h (x), ….
Теорема 1. 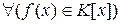 , где K – коммутативное кольцо с единицей, можно представить в виде:
, где K – коммутативное кольцо с единицей, можно представить в виде:
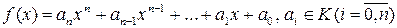 . (1)
. (1)
Доказательство. Обозначим через 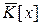 - множество всех многочленов из кольца K [ x ], представимых в виде (1). Так как для
- множество всех многочленов из кольца K [ x ], представимых в виде (1). Так как для 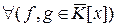
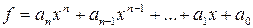 ,
, 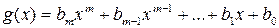 ,
, 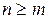 ,
, 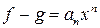
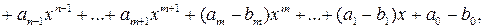
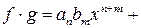
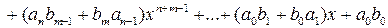 ,
,
то 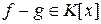 ,
, 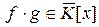 . Следовательно,
. Следовательно, 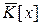 - подкольцо кольца K [ x ].
- подкольцо кольца K [ x ].
Так как 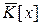 - кольцо, содержащее все элементы кольца K и x, а K [ x ] – минимальное кольцо, содержащее все элементы кольца K и элемент x, то
- кольцо, содержащее все элементы кольца K и x, а K [ x ] – минимальное кольцо, содержащее все элементы кольца K и элемент x, то 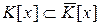 . Значит,
. Значит, 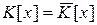 .
.
Определение. Представление многочлена 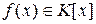 в виде (1) называется канонической (стандартной) формой многочлена f (x), если
в виде (1) называется канонической (стандартной) формой многочлена f (x), если
1) 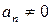 ;
;
2) в (1) нет подобных слагаемых;
3) слагаемые в представлении (1) расположены по убывающим на 1 степеням переменной x.
Теорема 2. Представление любого многочлена 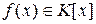 в канонической форме единственно.
в канонической форме единственно.
Пусть 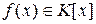 ,
, 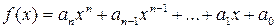 . Если
. Если 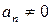 ,
,
то n называется степенью многочлена f (x). Будем считать, что степень нулевого
многочлена неопределена.
Свойства степени многочлена
Пусть 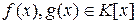 . Если
. Если 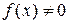 ,
, 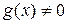 ,
, 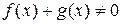 ,
,
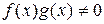 , то
, то
1. ст. 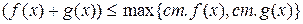 ,
,
2. 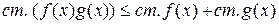 .
.
Если же 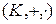 область целостности, то
область целостности, то
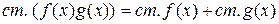 .
.
Деление многочлена на двучлен. Схема Горнера.
Пусть K [ x ] –кольцо многочленов над коммутативным кольцом K с единицей, 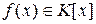 ,
, 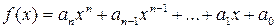 ,
, 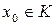 . Элемент
. Элемент 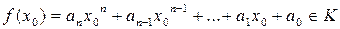 называется значением многочлена f (x) при x=x 0. Выясним вопрос деления многочлена f (x) на x-x 0,
называется значением многочлена f (x) при x=x 0. Выясним вопрос деления многочлена f (x) на x-x 0, 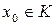 .
.
Теорема 3. Пусть 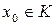 . Любой многочлен
. Любой многочлен 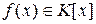 можно представить в виде
можно представить в виде
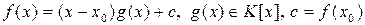 (2)
(2)
и притом единственным образом.
Доказательство. Пусть 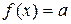 ,
, 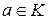 . Тогда
. Тогда 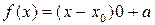 ,
, 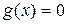 . Пусть теперь
. Пусть теперь 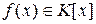 ,
, 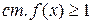 ,
, 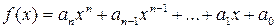 . Предположим, что
. Предположим, что 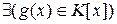 и
и 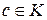 , что имеет место равенство (2). Из (2) следует, что
, что имеет место равенство (2). Из (2) следует, что 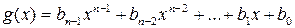 ,
, 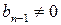 . С учетом выражения многочлена g (x) равенство (2) запишется:
. С учетом выражения многочлена g (x) равенство (2) запишется:
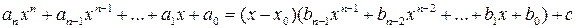
или
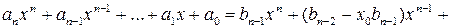
 (3)
(3)
Так как два многочлена 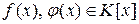 равны тогда и только тогда, когда их коэффициенты при соответствующих степенях переменной x равны, то
равны тогда и только тогда, когда их коэффициенты при соответствующих степенях переменной x равны, то
из (3) получим:
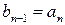 ,
,  ,
, 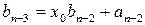 , …,
, …, 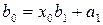 ,
, 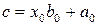 (4)
(4)
Равенствами (4) однозначно определяются многочлен 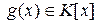 , и элемент
, и элемент 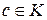 , для которых выполняется равенство (2). Из (2)
, для которых выполняется равенство (2). Из (2) 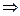 f (x 0)=c.
f (x 0)=c.
Теорема 4. Пусть 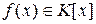 ,
, 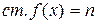 ,
, 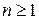 . Элемент
. Элемент 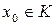 является корнем многочлена f (x)
является корнем многочлена f (x) 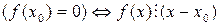 .
.
Вычисление коэффициентов многочлена g (x) и элемента 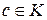 , удовлетворяющих равенству (2), удобно проводить по схеме Горнера:
, удовлетворяющих равенству (2), удобно проводить по схеме Горнера:
| a n | a n-1 | a n-2 | … | a 1 | a 0 | |
| x 0 | b n-1= a n | b n-2= x 0 b n-1+ a n-1 | b n-3= x 0 b n-2+ a n-2 | … | b 0= x 0 b 1+ a 1 | c = x 0 b 0+ a 0 |
Пример. Разделить многочлен f (x)= x 5+2 x 4+3 x +2 на x +1.
В этом примере x 0=-1. Составим таблицу:
| -1 | -1 |
Из таблицы следует, что f (x) = (x +1)(x 4+ x 3- x 2+ x +2).