С-1. ПЛОСКАЯ СИСТЕМА СИЛ. ВИДЫСВЯЗЕЙ. УСЛОВИЯ РАВНОВЕСИЯ
Определить реакции связей заданной конструкции (рисунок 1.12) при условиях нагружения указанных в таблице 1, где для сил F1, F2 указанны: модуль, направление, точка приложения; для равномерно распределённой нагрузки q указанны: величина, участок, на котором она действует и направление (знак «+» соответствует положительному направлению оси X или Y), также в таблице 1.1 указанны: величина крутящего момента М, масса груза Р, длина участка.
Таблица1.1
Исходные данные для задания С-1
        вариант
| I | II | III | |||||||
y 
α1
x
|  y
α2
x
| q, кН/м | М, кН×м | Р, кН | а, м | |||||
| F1=15 кН | F2= 25 кН | |||||||||
| Точка приложения | α1, град | Точка приложения | α2, град | Величина | Участок | Направление | ||||
| E | K | EC | + | 0.5 | ||||||
| K | E | CD | + | 0.6 | ||||||
| H | D | DH | + | 0.7 | ||||||
| D | H | DB | – | 0.8 | ||||||
| D | K | HB | – | 0.9 | ||||||
| H | E | KD | + | 1.0 | ||||||
| K | D | CK | – | 1.1 | ||||||
| E | H | AE | + | 1.2 | ||||||
| K | D | EC | – | 1.4 | ||||||
| E | H | CK | – | 1.5 | ||||||
| D | K | KD | + | 0.5 | ||||||
| H | E | DH | + | 0.6 | ||||||
| D | K | HB | – | 0.7 | ||||||
| K | H | CD | + | 0.6 | ||||||
| E | H | AC | – | 0.8 | ||||||
| H | D | DB | + | 0.9 | ||||||
| D | E | EC | – | 1.0 | ||||||
| K | H | KD | – | 1.1 |
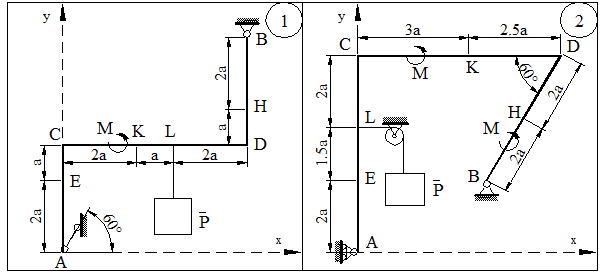
Рисунок 1.12
Рисунок 1.12 – продолжение
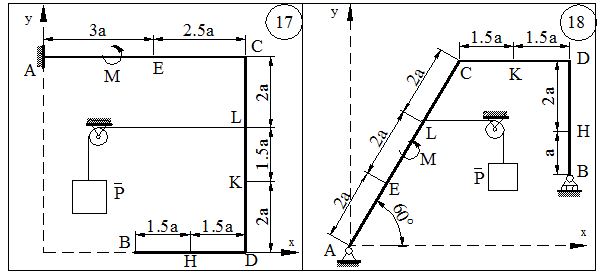
Рисунок 1.12 – окончание
Практическое занятие 2
Статически неопределимые системы.
Определение реакций опор составной конструкции (система двух тел)
2. Статически неопределимые системы [1,2,3,4,5]
Задача по определению реакций связей составной конструкции относится к статически неопределимым (рис. 2.1).
Рис. 2.1
Рисунок 2.1. а – в точке С шарнир, рис. 2.1. б – в точке С скользкая заделка.
Существуют два метода в решении таких задач:
1) рассматривают равновесие всей конструкции, получая три уравнения с четырьмя неизвестными 
, 
, 
, 
для (рис. 2.2 а, б), затем дополнительно рассмотрев условие равновесия левой (или правой) части конструкции. Действие отброшенной другой части при этом заменяют реакциями связи в месте соединения (рис. 2.2 а, б). Получим еще три уравнения, содержащих два новых неизвестных 
, 
для (рис. 2.2 а) или ; 
для (рис. 2.2 б). Решая полученную систему шести уравнений, находят все шесть неизвестных;
2) разделяют составную конструкцию в месте соединения на две части и рассматривают равновесие каждой из частей, заменяя действие отброшенной части реакциями соединения. Необходимо учесть, что реакции в соединении частей конструкции для каждой части будет противоположны по направлению и равны по величине (рис. 2.3 а, б).
Рис. 2.2
Рис. 2.3
Пример 2.1
Данная конструкция (рис.2.4) состоит из двух частей, соединенных промежуточным шарниром С.
На конструкцию действуют силы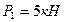 
; 
, а так же крутящий момент 
и равномерно распределенная нагрузка интенсивностью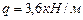 
.
Определить реакции связей данной конструкции.
Рис.2.4
.
Решение:
1) Проставим реакции отброшенных опор в точке А - подвижная цилиндрическая опора, ее реакция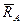 
, в точке В – жесткая заделка, ее реакции 
.
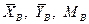2) Разделим конструкцию в месте промежуточного шарнира С на две части и рассмотрим равновесие ее левой части, заменив действие правой части реакциями в шарнире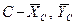 
, (рис.2.5). 
, 
.
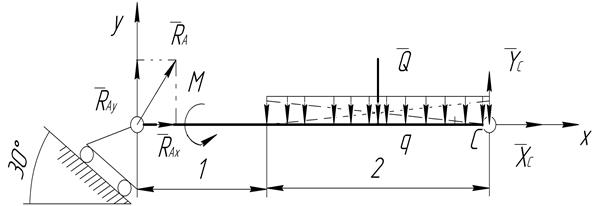
Рис.2.5
Составим уравнение равновесия для левой части конструкции:
; 
; 
;
; 
; 
;
. 
. 
.
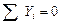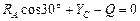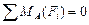Рассмотрим равновесие правой части конструкции, отбросив левую и, заменив ее действие реакциями в шарнире С (рис.2.6).
Рис.2.6
Составим уравнения равновесия для правой части конструкции:
; 
; 
;→
; 
; 
;→
; 
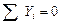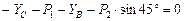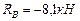; МВ=17,6 кНм.→
Решая систему шести уравнений с шестью неизвестными, определим реакции опор.
Ответ: ; ; 
; .
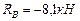Пример 2.2
Два стержня АС и ВD одинаковой длины шарнирно соединены в точке D и так же прикреплены к вертикальной стене в точках А и B (рис. 2.7). Стержень А С расположен горизонтально, стержень BD, образует угол 60° с вертикальной стеной. Стержень AC в точке Е. нагружен вертикальной силой P 1 = 40 Н и в точке С силой Q =100 Н, наклоненной к горизонту под углом 45°. Стержень BD в точке F нагружен вертикальной силой Р 2=40 Н.
Дано АЕ = ЕС; BF=FD; AC=BD определить реакцию шарниров А, В.
Решение:
За объект равновесия выберем стержни АС и ВD, шарнирно соединенные в точке D. К выбранному объекту приложены заданные силы 
, 
и 
. Освободив объект от связей, шарниров в точках А и В, получим объект находящийся в равновесии под действием системы заданных сил и реакций связей: 
~0.
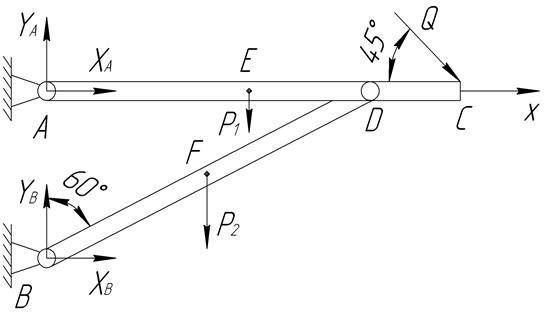
Рис. 2.7
Составим уравнение равновесия (рис. 2.7)
Получим 3 уравнения с 4 неизвестными 
. Рассмотрим равновесие одного из стержней, например BD (рис.2.8). К этому стержню дополнительно к указанным силам необходимо приложить силы в точке D, заменяющие действие стержня АС на BD:
;
.
Рис.2.8
Получим дополнительно три уравнения, но новых неизвестных два, следовательно, всего шесть уравнений с шестью неизвестными, решив которое, решим задачу.
Правильность решения можно проверить, рассмотреть равновесия стержня АС (рис. 2.9). По аксиоме о действии и противодействии 
, 
.
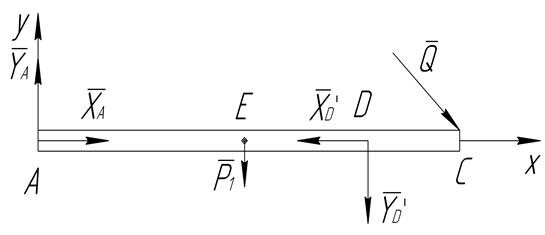
Рис. 2.9