Условия возрастания и убывания функции.
1) Для того чтобы дифференцируемая на интервале 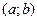 функция
функция  строго возрастала на этом интервале, достаточно, чтобы производная
строго возрастала на этом интервале, достаточно, чтобы производная  была положительна всюду на
была положительна всюду на 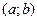 , т. е.
, т. е.

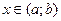 .
.
2) Для того чтобы дифференцируемая на интервале 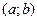 функция
функция  возрастала (не убывала) на этом интервале, необходимо и достаточно, чтобы производная
возрастала (не убывала) на этом интервале, необходимо и достаточно, чтобы производная  была неотрицательна всюду на
была неотрицательна всюду на 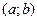 , т. е.
, т. е.

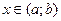 .
.
3) Аналогично, достаточным условием строгого убывания дифференцируемой функции  ,
, 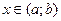 , является условие
, является условие
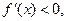
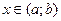 ;
;
необходимым и достаточным условием убывания — условие
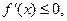
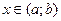 .
.
Экстремумы функции.
Точка  называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует окрестность точки
, если существует окрестность точки  , для всех точек которой верно неравенство
, для всех точек которой верно неравенство
 .
.
Если для всех  из некоторой окрестности точки
из некоторой окрестности точки  верно
верно
строгое неравенство
 ,
,
то точка  называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции  .
.
Аналогично, если в некоторой окрестности точки  выполняется
выполняется
неравенство
 ,
,
то точка  называется точкой локального минимума; если для всех
называется точкой локального минимума; если для всех
 из некоторой окрестности точки
из некоторой окрестности точки  верно строгое неравенство
верно строгое неравенство
( ,
,
то точка  называется точкой строгого локального минимума.
называется точкой строгого локального минимума.
Необходимое условие экстремума. Если  – точка экстремума функции
– точка экстремума функции  , то
, то  или
или  – не дифференцируемая в точке
– не дифференцируемая в точке  . Точку
. Точку  называют критической точкой функции
называют критической точкой функции  , если
, если  , или
, или  – не дифференцируемая в точке
– не дифференцируемая в точке  .
.
Первое достаточное условие экстремума. Пусть функция  дифференцируемая в проколотой окрестности точки
дифференцируемая в проколотой окрестности точки  и непрерывна в точке
и непрерывна в точке  . Тогда:
. Тогда:
1) если 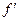 меняет знак с «+» на «-» в точке
меняет знак с «+» на «-» в точке  , то
, то  - точка максимума функции
- точка максимума функции  ;
;
2) если 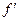 меняет знак с «-» на «+» в точке
меняет знак с «-» на «+» в точке  , то
, то  - точка минимума функции
- точка минимума функции  .
.
Второе достаточное условие экстремума. Пусть функция  дважды дифференцируемая в проколотой окрестности точки
дважды дифференцируемая в проколотой окрестности точки  и
и  . Тогда:
. Тогда:
1) если  , то
, то  - точка максимума функции
- точка максимума функции  ;
;
2) если 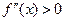 , то
, то  - точка минимума функции
- точка минимума функции  .
.
Если функция  непрерывна на отрезке
непрерывна на отрезке 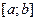 , то свои глобальные экстремумы (наибольшее и наименьшее значение функции) эта функция имеет либо в критических точках, либо на концах отрезка.
, то свои глобальные экстремумы (наибольшее и наименьшее значение функции) эта функция имеет либо в критических точках, либо на концах отрезка.
Пример 1. Исследовать на монотонность и экстремум функцию  .
.
Решение.  определена при всех
определена при всех  . По формуле производной произведения
. По формуле производной произведения  ;
;
 и
и  - критические точки
- критические точки  . На верхней оси рис.1 обозначено распределение знаков
. На верхней оси рис.1 обозначено распределение знаков  , а на нижней – поведение функции
, а на нижней – поведение функции  .
.
Ответ. В интервалах   монотонно возрастает ( монотонно возрастает ( ), в интервале ), в интервале  монотонно убывает, монотонно убывает,
|
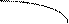 
 
   
   
Рис. 1 |
 - точка максимума с
- точка максимума с 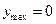 ,
,  - точка минимума с
- точка минимума с  .
.
Условия выпуклости. Точки перегиба.
Дифференцируемая функция  называется выпуклой вверх (вогнутой вниз) на некотором интервале
называется выпуклой вверх (вогнутой вниз) на некотором интервале 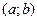 , если
, если  ее график на отрезке
ее график на отрезке  расположен не ниже (не выше) хорды
расположен не ниже (не выше) хорды  , где
, где  ,
,  , то есть
, то есть
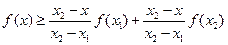
 .
.
Условия выпуклости функции. Для того чтобы функция  , дважды дифференцируемая на интервале
, дважды дифференцируемая на интервале 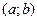 , была выпуклой вниз на этом интервале, необходимо и достаточно, чтобы вторая производная
, была выпуклой вниз на этом интервале, необходимо и достаточно, чтобы вторая производная  была неотрицательна на
была неотрицательна на 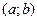 , т. е.
, т. е.
 ,
, 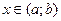 .
.
Условие
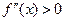 ,
, 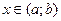 ,
,
является достаточным условием строгой выпуклости вниз функции  на интервале
на интервале 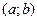 .
.
Аналогично, для функции  , имеющей на интервале
, имеющей на интервале 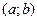 вторую производную, необходимым и достаточным условием выпуклости вверх на этом интервале является условие
вторую производную, необходимым и достаточным условием выпуклости вверх на этом интервале является условие
 ,
, 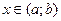 ,
,
а достаточным условием строгой выпуклости вверх — условие
 ,
, 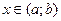 .
.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , непрерывна в точке
, непрерывна в точке  и имеет в этой точке конечную или бесконечную производную. Тогда если функция
и имеет в этой точке конечную или бесконечную производную. Тогда если функция  при переходе через точку
при переходе через точку  меняет направление выпуклости, то точка
меняет направление выпуклости, то точка  называется точкой перегиба функции
называется точкой перегиба функции  . В этом случае точку (
. В этом случае точку ( ;
;  ) называют точкой перегиба графика функции
) называют точкой перегиба графика функции  .
.
Необходимое условие точки перегиба. Если точка  является точкой перегиба функции
является точкой перегиба функции  , то либо
, то либо  = 0, либо
= 0, либо  не существует.
не существует.
Достаточное условие точки перегиба. Пусть функция  дифференцируема в точке
дифференцируема в точке  и дважды дифференцируема в некоторой окрестности точки
и дважды дифференцируема в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  . Тогда точка
. Тогда точка  является точкой перегиба функции
является точкой перегиба функции  , если существует окрестность точки
, если существует окрестность точки  , в которой либо
, в которой либо
 при
при  и
и 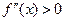 при
при  ,
,
либо
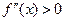 при
при  и
и  при
при  .
.
В этом случае принято говорить, что при переходе через точку  вторая производная меняет знак.
вторая производная меняет знак.
Пример 2. Исследовать на выпуклость, вогнутость и точки перегиба функцию  .
.
Решение. Надлежит исследовать знак второй производной. Имеем:
 ,
, 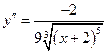 ;
;
 нигде не обращается в ноль, но меняет знак в точке
нигде не обращается в ноль, но меняет знак в точке  . Знаки
. Знаки  указаны на рис. 2;
указаны на рис. 2;  — абсцисса точки перегиба,
— абсцисса точки перегиба,  .
.
На  функция
функция  вогнутая, на
вогнутая, на  выпуклая.
выпуклая.
 

  
|

  
 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 2 Рис. 3
Пример 3. Исследовать на выпуклость, вогнутость и точки перегиба функцию  .
.
Решение. Имеем:  ;
;  .
.
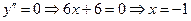 .
.
Знаки  указаны на числовой прямой (рис. 3).
указаны на числовой прямой (рис. 3).
Ответ. На интервале 
 выпуклая вверх, на интервале
выпуклая вверх, на интервале
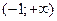
 вогнутая вниз,
вогнутая вниз, 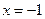 — абсцисса точки перегиба и
— абсцисса точки перегиба и  .
.