9. Сложное движение. Основные теоретические положения [1,4,5,6]
Относительным движением называется движение точки относительно подвижной системы координат.
Переносным движением называют движение точки вместе с подвижной системой относительно неподвижной.
Абсолютная скорость точки определяется:
. (9.1)
Если 
Если 
Абсолютное ускорение точки определяется:
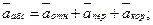(9.2)
Относительное и переносное ускорения раскладывают на составляющие (нормальную и тангенциальную) в зависимости от вида и траектории движения.
Кориолисово ускорение определяется:
(9.3)
В скалярной форме: 
Направление Кориолисова ускорения определяются следующим образом: чтобы получить вектор кориолисова ускорения необходимо вектор относительной скорости спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию на 900 в сторону переносного движения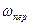 
[1].
Вектор угловой скорости тела направляется вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки.
Величина абсолютного ускорения определяется путем проецирование векторного равенства 9.2 на оси координат.
Пример 9.1
По заданным уравнениям относительного движения точки М переносного движения тела D для момента времени 
определить абсолютную скорость и абсолютное ускорение точки М [ 11].
Дано: схема механизма (рис. 9.1):
О1А=О2В=20 см; R=16 см; 
рад; 
см; 
с.
Решение:
Найдем положение тела D и точки М в заданный момент времени. Положение тела D определяется углом 
. При 
с.
рад.
Положение точки М на теле D можно определить углом:
При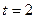 
с:
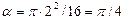рад.
Тело D и точка М в заданный момент времени показаны на (рис.9.1). Абсолютную скорость точки М определяем как геометрическую сумму относительной и переносной скоростей:
Модуль относительной скорости точки М:
.
Здесь 
- проекция относительной скорости на касательную к траектории относительного движения.
.
При 
с
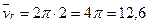см/с.
Следовательно: 
см/с.
Положительный знак показывает, что относительное движение точки происходит в направлении положительного отсчета 
. Вектор относительной скорости показан на (рис.9. 2). Переносную скорость определяем, учитывая, что
, 
,
где 
- модуль угловой скорости звена 
.
Обозначая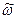 
алгебраическую величину угловой скорости, имеем:
c-1.
При с
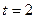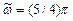с-1.
Так как 
, то:
с-1.
Положительный знак у величины 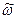показывает, что вращение звена О1A происходит в направлении возрастания угла 
.
Модуль переносной скорости
см/с.
Вектор 
направлен перпендикулярно к звену О1А в сторону его вращения.
Рис.9.1
Модуль абсолютной скорости точки М найдем способом проекций. Как следует из (рис. 9.2):
; 
.
Следовательно,
см/с; 
см/с; 
см/с.
Рис.9.2
Абсолютное ускорение точки при поступательном переносном движении равно геометрической сумме относительного и переносного ускорений:
;
или в развернутом виде
.
Модуль относительного касательного ускорения
; 
.
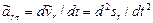В рассматриваемом случае
см/с2; 
см/с2.
Рис.9.3
Положительный знак у величины 
показывает, что вектор направлен в сторону положительного отсчета 
, т. е. так же, как 
, (относительное движение - ускоренное), рис. 9.3.
Относительное нормальное ускорение
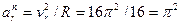см/с2.
Вектор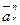 
направлен по радиусу к центру кривизны траектории относительного движения точки M.
Переносное вращательное ускорение
; 
,
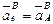где 
- модуль углового ускорения звена О1А
.
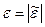Здесь 
- алгебраическая величина углового ускорения.
В рассматриваемом случае:
с-2.
Совпадения знаков у величин 
, и 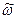показывает, что вращение тела D ускоренное:
c-2;
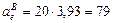см/с2.
Направление 
соответствует направлению 
(см. рис. 3). Переносное центростремительное ускорение:
см/с2.
Вектор 
направлен от А к О1, а 
имеет одинаковое с ним направление.
Модуль абсолютного ускорения находим способом проекций:
,
,
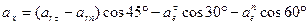или после вычислений,
см/с2 ; 
,
см/с2.
Практическое занятие 10